Binomna raspodjela: definicija, formula, primjeri

Teorija vjerojatnosti je nevidljivo prisutna u našim životima. Ne obraćamo pažnju na to, ali svaki događaj u našem životu ima određenu vjerojatnost. Uzimajući u obzir veliki broj scenarija, za nas postaje nužno odrediti najvjerojatnije i najmanje vjerojatno od njih. Najpogodnije je grafički analizirati takve vjerojatnosne podatke. Distribucija nam može pomoći u tome. Binomni - jedan od najjednostavnijih i najtočnijih.

Prije nego što se izravno okrenemo matematici i teoriji vjerojatnosti, pozabavimo se onima koji su prvi došli do ove vrste distribucije i kakva je povijest razvoja matematičkog aparata za taj koncept.

Povijest

Pojam vjerojatnosti poznat je još od antičkih vremena. Međutim, drevni matematičari tome nisu pridavali veliku važnost i mogli su postaviti samo temelje za teoriju, koja je kasnije postala teorija vjerojatnosti. Stvorili su neke kombinatorne metode koje su uvelike pomogle onima koji su kasnije stvorili i razvili samu teoriju.

U drugoj polovici 17. stoljeća započinje formiranje osnovnih pojmova i metoda teorije vjerojatnosti. Uvedene su definicije slučajnih varijabli, metode izračuna vjerojatnosti jednostavnih i nekih složenih neovisnih i ovisnih događaja. Takvo zanimanje za slučajne varijable i vjerojatnosti diktiralo je kockanje: svi su željeli znati koje su mu šanse za pobjedu.

Sljedeći korak bio je primjena metoda u teoriji vjerojatnosti matematička analiza. Eminentni matematičari, kao što su Laplace, Gauss, Poisson i Bernoulli, preuzeli su taj zadatak. Oni su ovo područje matematike prešli na novu razinu. Upravo je James Bernoulli otkrio zakon o binomnoj distribuciji. Usput, kao što ćemo kasnije saznati, na temelju tog otkrića napravljeno je još nekoliko, što je omogućilo stvaranje zakona normalne distribucije i još mnogo toga.

Sada, prije nego što počnemo opisivati ​​distribuciju binomnog dijela, malo ćemo osvježiti pojmove teorije vjerojatnosti, vjerojatno već zaboravljene iz škole.

Osnove teorije vjerojatnosti

Razmotrit ćemo takve sustave, zbog kojih su moguća samo dva ishoda: "uspjeh" i "neuspjeh". To je lako razumjeti na primjeru: bacamo novčić, pretpostavljajući da će repovi ispasti. Vjerojatnosti svakog od mogućih događaja (repovi ispadaju - "uspjeh", orao ispadne - "nije uspjeh") su 50 posto s savršenim balansiranjem novčića i odsutnošću drugih čimbenika koji mogu utjecati na eksperiment.

Bio je to najjednostavniji događaj. Međutim, postoje i složeni sustavi u kojima se izvode sekvencijalni postupci, a vjerojatnosti ishoda tih akcija varirat će. Na primjer, razmislite o takvom sustavu: u kutiji, čiji sadržaj ne možemo vidjeti, nalazi se šest apsolutno identičnih kuglica, tri para plave, crvene i bijele. Moramo nasumce uzeti nekoliko lopti. Sukladno tome, povlačenjem jedne od bijelih kuglica, s vremena na vrijeme smanjit ćemo vjerojatnost da će i sljedeća dobiti bijelu kuglu. To se događa zato što se broj objekata u sustavu mijenja.

U sljedećem ćemo poglavlju razmotriti složenije matematičke koncepte koji nas usko vode do riječi "normalna distribucija", "binomna raspodjela" i slično.

Elementi matematičke statistike

U statistici, koja je jedno od područja primjene teorije vjerojatnosti, postoji mnogo primjera gdje podaci za analizu nisu dati eksplicitno. To jest, ne u numeričkom, već u obliku podjele prema znakovima, na primjer, prema spolu. Kako bi se matematički aparat primijenio na takve podatke i izvukao zaključke iz dobivenih rezultata, potrebno je pretvoriti izvorne podatke u numerički oblik. U pravilu, da bi se to postiglo, pozitivnom se ishodu dodjeljuje vrijednost 1, a negativnoj se dodjeljuje vrijednost 0. Tako dobivamo statističke podatke koji se mogu analizirati matematičkim metodama.

Sljedeći korak u razumijevanju što je binomna raspodjela slučajne varijable je određivanje varijance slučajne varijable i matematičkog očekivanja. O tome se raspravlja u sljedećem odjeljku.

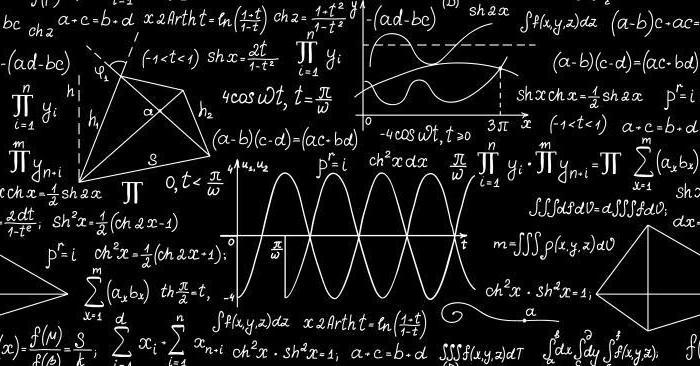
Matematičko očekivanje

Zapravo, lako je razumjeti što je to očekivanje. Razmotrite sustav u kojem postoji mnogo različitih događaja s različitim vjerojatnostima. Matematičko očekivanje će se zvati vrijednost jednaka zbroju proizvoda vrijednosti tih događaja (i matematičkog oblika, o čemu smo raspravljali u posljednjem odjeljku) o vjerojatnosti njihove provedbe.

Matematičko očekivanje binomne raspodjele izračunava se prema istoj shemi: uzimamo vrijednost slučajne varijable, pomnožimo je s vjerojatnošću pozitivnog ishoda, a zatim sumiramo dobivene podatke za sve količine. Vrlo je prikladno grafički prikazati ove podatke - tako se bolje uočava razlika između matematičkih očekivanja različitih veličina.

U sljedećem odjeljku reći ćemo vam nešto o drugom konceptu - varijanci slučajne varijable. Također je usko povezana s takvim konceptom kao binomna razdioba vjerojatnosti i njegova je karakteristika.

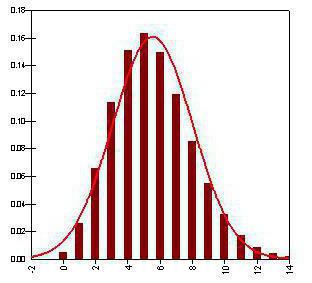
Varijanca binomne distribucije

Ta je vrijednost usko povezana s prethodnom i karakterizira distribuciju statističkih podataka. On predstavlja prosječan kvadrat odstupanja vrijednosti od njihovog očekivanja. To jest, varijanca slučajne varijable je zbroj kvadrata razlika između vrijednosti slučajne varijable i njenog očekivanja, pomnožene s vjerojatnošću tog događaja.

Općenito, ovo je sve što trebamo znati o varijansi da bi se razumjelo što je binomna razdioba vjerojatnosti. Sada se izravno osvrćemo na našu glavnu temu. Naime, ono što se krije iza tako naizgled složene fraze "binomni zakon o raspodjeli".

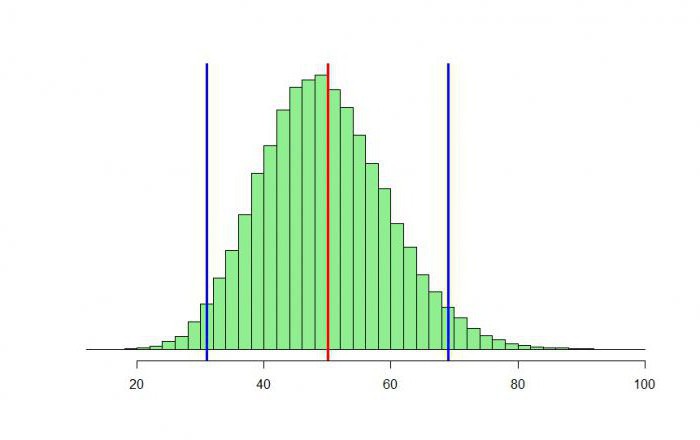
Binomna raspodjela

Najprije ćemo razumjeti zašto je ova raspodjela binomna. Ona dolazi od riječi "bin". Možda ste čuli za Newtonov binomni - formulu s kojom možete zbrojiti dva proizvoljna broja a i b u bilo koji ne-negativni stupanj n.

Kao što ste vjerojatno već pogodili, Newtonova binomna formula i binomna distribucijska formula su gotovo identične formule. Jedina iznimka je da druga ima primijenjenu vrijednost za određene količine, a prva je samo opći matematički alat, čije primjene u praksi mogu biti različite.

Formula za distribuciju

Binomna funkcija raspodjele može se napisati kao zbroj sljedećih članova:

(n! / (nk)! k!) * p ^k * q ^nk

Ovdje n je broj neovisnih slučajnih eksperimenata, p je broj uspješnih ishoda, q je broj neuspješnih ishoda, k je broj eksperimenta (može uzeti vrijednosti od 0 do n),! - oznaka faktorijalnog, takva funkcija broja, čija je vrijednost jednaka proizvodu svih brojeva koji ga dosežu (na primjer, za broj 4: 4! = 1 * 2 * 3 * 4 = 24).

Osim toga, funkcija binomne raspodjele može se napisati kao nepotpuna beta funkcija. Međutim, ovo je složenija definicija, koja se koristi samo u rješavanju složenih statističkih problema.

Binomna raspodjela, primjeri kojih smo razmatrali gore, jedna je od najjednostavnijih vrsta raspodjele u teoriji vjerojatnosti. Tu je i normalna distribucija, koja je vrsta binomnog. Najčešće se koristi, a najjednostavnije u izračunima. Tu je i Bernoullijeva distribucija, Poissonova distribucija, uvjetna raspodjela. Svi oni grafički opisuju vjerojatnosti procesa pod različitim uvjetima.

U sljedećem ćemo poglavlju razmotriti aspekte vezane uz korištenje ovog matematičkog aparata u stvarnom životu. Na prvi pogled, naravno, čini se da je to još jedna matematička stvar, koja, kao i obično, ne pronalazi primjenu u stvarnom životu, i općenito nije potrebna nikome osim samim matematičarima. Međutim, ovo je daleko od slučaja. Uostalom, sve vrste distribucija i njihovi grafički prikazi stvoreni su isključivo za praktične svrhe, a ne kao hir znanstvenika.

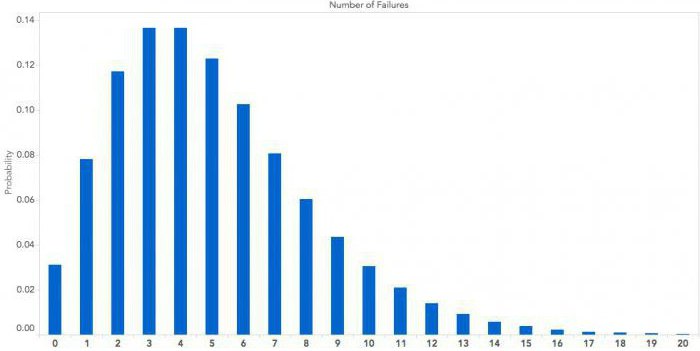
primjena

Naravno, najvažnija uporaba distribucije pronađena u statistici, jer im je potrebna sveobuhvatna analiza skupa podataka. Kao što praksa pokazuje, vrlo veliki broj polja podataka ima približno jednaku raspodjelu vrijednosti: kritična područja vrlo niskih i vrlo visokih vrijednosti, u pravilu sadrže manje elemenata od prosječnih vrijednosti.

Analiza velikih količina podataka potrebna je ne samo u statistici. Neophodna je, na primjer, u fizičkoj kemiji. U ovoj se znanosti koristi za određivanje mnogih veličina koje su povezane sa slučajnim oscilacijama i kretanjima atoma i molekula.

U sljedećem poglavlju, pogledajmo koliko je važna uporaba takvih statističkih koncepata kao binomna raspodjela slučajne varijable u svakodnevnom životu za vas i mene.

Zašto mi to treba?

Mnogi ljudi postavljaju ovo pitanje kada je u pitanju matematika. I usput, matematika se ne naziva kraljicom znanosti. Ona je temelj fizike, kemije, biologije, ekonomije, au svakoj od tih znanosti primjenjuje se i neka distribucija: nije li ova diskretna binomna raspodjela, ili normalna, važna. A ako bolje pogledamo svijet oko sebe, vidjet ćemo da se matematika koristi svugdje: u svakodnevnom životu, na poslu, pa čak i ljudskim odnosima mogu se predstaviti kao statistički podaci i analizirati (usput, oni koji rade u posebne organizacije koje prikupljaju informacije).

Sada ćemo malo razgovarati o tome što učiniti ako trebate znati više o ovoj temi nego što smo naveli u ovom članku.

Što još možete pročitati?

Informacije koje smo dali u ovom članku su daleko od potpunog. Postoji mnogo nijansi u vezi s onim što oblik distribucije može potrajati. Binomna raspodjela, kao što smo već otkrili, jedna je od glavnih vrsta na kojoj se temelje sve matematičke statistike i teorija vjerojatnosti.

Ako ste zainteresirani, ili u vezi s vašim poslom, morate znati mnogo više o ovoj temi, trebat ćete studirati stručnu literaturu. Trebali bismo početi s sveučilišnim tečajem matematičke analize i otići na dio teorije vjerojatnosti. Također će biti korisno znanje u području serije, jer je binomna razdioba vjerojatnosti samo niz uzastopnih članova.

zaključak

Prije završetka članka želimo ispričati još jednu zanimljivost. To se izravno odnosi na temu našeg članka i cjelokupnu matematiku.

Mnogi ljudi tvrde da je matematika beskorisna znanost, i ništa što su prošli u školi nije im dobro došlo. Ali znanje nikada nije suvišno, a ako vam nešto u životu nije korisno, to znači da ga se jednostavno ne sjećate. Ako imate znanje, oni vam mogu pomoći, ali ako ih nema, onda nema potrebe čekati pomoć od njih.

Dakle, pogledali smo koncept binomne raspodjele i sve srodne definicije i govorili o tome kako se to odnosi na naš život.