Podjela na nulu. Fascinantna matematika

Broj 0 može se predstaviti kao neka vrsta granice koja odvaja svijet realnih brojeva od imaginarnih ili negativnih. Zbog nejasne pozicije, mnoge operacije s ovom brojčanom vrijednošću nisu predmet matematičke logike. Živi primjer je nemogućnost podjele na nulu. A riješene aritmetičke operacije s nulom mogu se izvesti pomoću općeprihvaćenih definicija.

Povijest nule

Nula je referentna točka u svim standardnim sustavima računanja. Europljani su počeli koristiti taj broj relativno nedavno, ali mudraci Drevna Indija nula tisuću godina prije nego što su europski matematičari redovito koristili prazan broj. Čak i prije Indijanaca, nula je bila obvezna količina u numeričkom sustavu Maya. Taj je Amerikanac koristio račun duodenala, a sa nulom su započeli prvi dan svakog mjeseca. Zanimljivo je da se u Mayi znak koji označava “nulu” potpuno poklapa sa znakom koji definira “beskonačnost”. Tako su drevne Maja zaključile da su te količine identične i nepoznate.

Matematičke operacije s nulom

Standardne matematičke operacije s nulom mogu se svesti na nekoliko pravila.

Dodatak: ako se dodaje nula proizvoljnom broju, tada neće promijeniti svoju vrijednost (0 + x = x).

Oduzimanje: kada se oduzme nula od bilo kojeg broja, vrijednost oduzete ostaje nepromijenjena (x-0 = x).

Množenje: bilo koji broj pomnožen s 0 daje 0 u proizvodu (a * 0 = 0).

Podjela: nula se može podijeliti s bilo kojim brojem koji nije jednak nuli. U tom slučaju, vrijednost takve frakcije će biti 0. A podjela na nulu je zabranjena.

Potenciranje. Ova radnja se može izvesti s bilo kojim brojem. Proizvoljan broj podignut na stupanj nula će dati 1 (x ⁰ = 1).

Nula je 0 na bilo koji stupanj (0a = 0).

U ovom slučaju odmah dolazi do kontradikcije: izraz 0 ⁰ nema smisla.

Paradoks matematike

Činjenica da je podjela na nulu nemoguća, mnogi ljudi znaju iz škole. Ali iz nekog razloga nemoguće je objasniti razlog takve zabrane. Zapravo, zašto ne postoji formula za podjelu na nulu, ali su druge akcije s tim brojem sasvim razumne i moguće? Odgovor na ovo pitanje daju matematičari.

Stvar je u tome da uobičajene aritmetičke operacije koje učenici uče u osnovnoj školi zapravo nisu jednake u pravima, kao što nam se čini. Sve jednostavne operacije s brojevima mogu se svesti na dva: zbrajanje i množenje. Te radnje čine suštinu samog pojma broja, dok se preostale operacije temelje na korištenju ova dva.

Dodavanje i umnožavanje

Uzmite standardni primjer oduzimanja: 10-2 = 8. U školi se smatra jednostavno: ako se od deset predmeta oduzmu dvije stavke, osam će ostati. Ali matematičari gledaju na ovu operaciju sasvim drugačije. Naposljetku, takva operacija kao oduzimanje za njih ne postoji. Ovaj primjer može se napisati na drugi način: x + 2 = 10. Za matematičare je nepoznata razlika samo broj koje treba dodati na dva da bi se dobilo osam. I ovdje nije potrebno oduzimanje, samo trebate pronaći odgovarajuću numeričku vrijednost.

Množenje i podjela smatraju se istim. U primjeru 12: 4 = 3, može se razumjeti da se radi o podjeli osam objekata na dvije jednake skupine. Ali u stvarnosti to je samo obrnuta formula zapisa 3x4 = 12. Takvi primjeri podjele mogu se dati beskrajno.

Primjeri podjele na 0

Ovdje postaje malo jasno zašto je nemoguće podijeliti je na nulu. Množenje i podjela na nulu pokorava se vlastitim pravilima. Svi primjeri podjele te količine mogu se formulirati kao 6: 0 = x. Ali to je obrnuti zapis izraza 6 * x = 0. Ali, kao što znate, bilo koji broj pomnožen s 0 daje samo 0 u proizvodu.Ovo svojstvo je svojstveno samom pojmu nulte vrijednosti.

Ispada da ne postoji takav broj koji, pomnožen s 0, daje bilo kakvu opipljivu vrijednost, odnosno taj zadatak nema rješenja. Ovaj odgovor ne treba se bojati, to je prirodan odgovor za zadatke ove vrste. Samo pisanje 6: 0 nema smisla, a ona ništa ne može objasniti. Ukratko, taj se izraz može objasniti besmrtnom "podjelom na nulu".

Postoji li operacija 0: 0? Doista, ako je operacija množenja s 0 legalna, može li se nula podijeliti s nulom? Uostalom, jednadžba oblika 0x 5 = 0 potpuno je zakonita. Umjesto broja 5, možete staviti 0, proizvod ovog neće se promijeniti.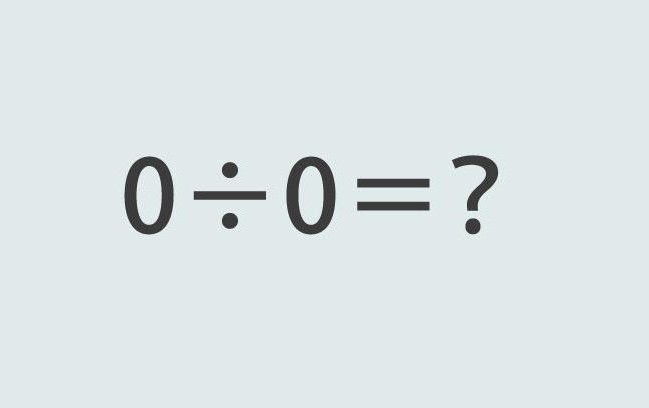

Doista, 0x0 = 0. Ali još uvijek je nemoguće podijeliti s 0. Kao što je spomenuto, podjela je jednostavno inverzno množenje. Dakle, ako u primjeru 0x5 = 0, moramo odrediti drugi faktor, dobivamo 0x0 = 5. Ili 10. Ili beskonačnost. Dijeljenje beskonačnosti s nulom - kako vam se sviđa?

Ali ako se bilo koji broj uklapa u izraz, onda to nema smisla, ne možemo odabrati jednu iz beskonačnog skupa brojeva. A ako je tako, to znači da izraz 0: 0 nema smisla. Ispada da se i sama nula ne može podijeliti s nulom.

Viša matematika

Podjela na nulu je glavobolja za školsku matematiku. Studirao je na tehničkim sveučilištima matematička analiza malo proširuje koncept zadataka koji nemaju rješenje. Na primjer, na već poznati izraz 0: 0 dodaju se nove koje nemaju rješenje u školskim matematičkim kolegijima:

• beskonačnost podijeljena beskonačnošću: ∞: ∞;
• beskonačnost minus beskonačnost: ∞ - ∞;
• jedinica podignuta do beskonačne snage: 1 ^∞ ;
• beskonačnost pomnožena s 0: 0 * 0;
• neke druge.

Elementarne metode za rješavanje takvih izraza nije moguće. Ali viša matematika, zbog dodatnih mogućnosti za niz sličnih primjera, daje konačna rješenja. To je osobito vidljivo u razmatranju problema iz teorije granica.

Objavljivanje nesigurnosti

U teoriji granica vrijednost 0 zamjenjuje se uvjetnom beskonačno malom varijablom. Izrazi u kojima se podjela na nulu dobiva zamjenom željene vrijednosti se pretvaraju. U nastavku je standardni primjer otkrivanja ograničenja pomoću uobičajenih algebarskih transformacija:

Kao što se može vidjeti u primjeru, jednostavno smanjenje frakcije rezultira njegovom vrijednošću do potpuno racionalnog odgovora.

Pri razmatranju granica trigonometrijskih funkcija, njihovi izrazi teže biti svedeni na prvu značajnu granicu. Pri razmatranju granica u kojima imenitelj prelazi na 0 pri postavljanju granice, upotrijebite drugu izvanrednu granicu.

L'Hôpital metoda

U nekim slučajevima granice izraza mogu se zamijeniti granicom njihovih izvedenica. Guillaume Lopital - francuski matematičar, utemeljitelj francuske škole matematičke analize. Dokazao je da su granice izraza jednake granicama izvedenica tih izraza. U matematičkom pisanju, njegovo je pravilo kako slijedi.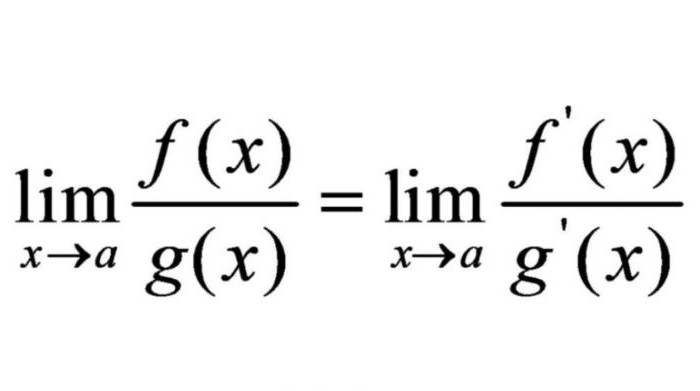

Trenutno se L'Hôpital metoda uspješno koristi u rješavanju nesigurnosti tipa 0: 0 ili ∞: ∞.