Slobodne vibracije. Opće informacije

U ovom članku govorit ćemo o slobodnim oscilacijama. Razmotrite njihove primjere: matematički i opružni klatni, kao i oscilirajući krug.

Mehaničke vibracije

Oscilatorno gibanje ili mehanička oscilacija naziva se kretanjem tijela ili promjenom stanja, koje se ponavlja s vremenom. Primjeri u mehanici mogu biti oscilacije klatna, žica, balansera satova, zvučničkih membrana, mostova i drugih konstrukcija.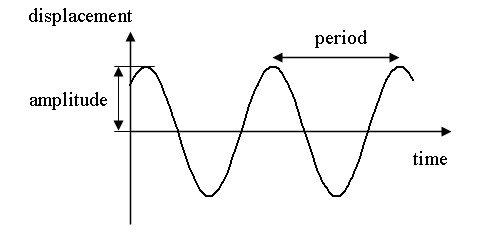

Oscilatorno gibanje naziva se periodično ako se vrijednosti fizičkih veličina koje se mijenjaju tijekom oscilacija ponavljaju u jednakim vremenskim razmacima.

Minimalni interval (interval) vremena nakon kojeg se položaj tijela ponavlja tijekom oscilatornog gibanja naziva se razdoblje oscilacije T. Broj oscilacija koje tijelo izvodi po jedinici vremena naziva se frekvencija oscilacija ν .

harmonik

Među različitim oscilatornim gibanjima važni su harmonijski oscilatorni pokreti.

Harmonika se naziva oscilacija, tijekom koje materijalna točka odstupa od ravnotežnog položaja prema zakonu sinusa ili kosinusa.

Važnost ovog pokreta leži u činjenici da su mnoga oscilatorna kretanja u prirodi blizu harmonijskog, a također i zato što se složene vibracije mogu razložiti na harmonijske. Pišemo pomicanje materijalne točke tijekom harmonijskog gibanja:

x = Asin (ωt + φ ₀ )

Slovo " x" označava odstupanje točke koja oscilira iz ravnotežnog položaja. Maksimalni pomak iz ravnotežnog položaja naziva se amplituda. U našem slučaju, x _max = A. Argument (ωt +) ₀ ) naziva se faza oscilacija, a vrijednost. ₀ - početna faza oscilacija. Faza omogućuje određivanje pomaka točke u određenom vremenskom trenutku.

Razdoblje harmonijske oscilacije T , s obzirom na to razdoblje oscilacija faza će se promijeniti u 2π , može se izračunati pomoću formule:

T = 2π / ω.

Frekvencija slobodnih oscilacija je:

ν = 1 / T = ω / 2π.

Brzina točke s harmoničkim oscilacijama nalazi se kao prva izvedenica vremenskog pomaka:

v = dx / dt = Aωcos (ωt + φ ₀ ).

Ubrzanje točke s harmonijskim oscilacijama nalazi se kao druga izvedenica vremenskog pomaka:

a = dv / dt = Aω ² cos (ωt + φ ₀ ).

besplatno

Ako se tijelo u oscilatornom sustavu izvuče iz ravnoteže i oslobodi, tada će provesti tzv. Slobodne oscilacije, koje su uvijek prigušene.

Za proučavanje oscilacija različite prirode često se koriste uređaji koji se nazivaju osciloskopi. Osciloskop (od latinskog. Oscillo - "oklijeva" i grčki. Graf - "pisati") - uređaj za promatranje oscilacija i snimanje u grafičkom obliku.

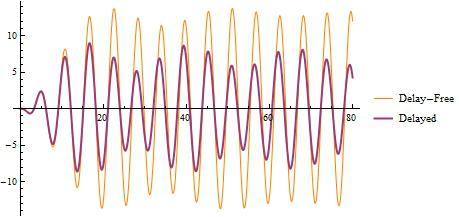
Amplituda oscilacija u realnim sustavima se smanjuje s vremenom, a oscilacije, na kraju, prestaju, stoga su slobodne oscilacije uvijek prigušene.

Period oscilacija ne ovisi o njihovoj amplitudi, jer u stvarnim mehaničkim sustavima uvijek postoji gubitak mehaničke energije.

Ispitivanje slobodnih oscilacija u sustavu "opterećenje - opruga", u nedostatku gubitaka mehanička energija može se zaključiti da se razdoblje takvih oscilacija određuje pomoću formule:

T = 2π / ω,

gdje je ω ciklička frekvencija.

Frekvencija slobodnih oscilacija mjeri se formulom:

ν = 1 / T = ω / 2π.

Math Pendulum

Matematičko klatno se smatra točkovnim tijelom koje je suspendirano od neraskidive i bestežinske niti. Matematički klatno je apstraktan pojam, jer, prvo, u prirodi nema točkastih tijela, i drugo, nema apsolutno neraskidivih i bestežinskih niti. Međutim, uz određenu aproksimaciju, matematički klatno se može smatrati kuglom koja je suspendirana s konca. Kada je lopta u stanju ravnoteže, na nju djeluju sila gravitacije i sila elastičnosti niti, koja se međusobno uravnotežuju, drugim riječima, rezultanta tih sila je nula.

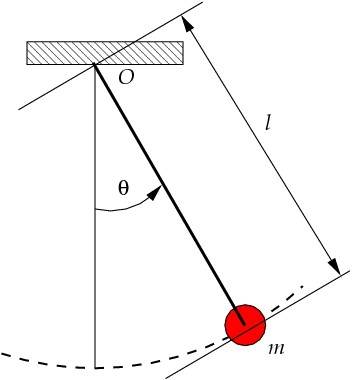
Period oscilacija matematičkog njihala može se izračunati pomoću formule:

T = 2π / ω,

gdje je ciklička frekvencija slobodnih oscilacija ω ² = l / g, a l duljina niti.

Prema formuli, može se zaključiti da razdoblje oscilacija matematičkog klatna ne ovisi o tjelesnoj težini, već je određeno samo duljinom suspenzije i ubrzanjem slobodnog pada.

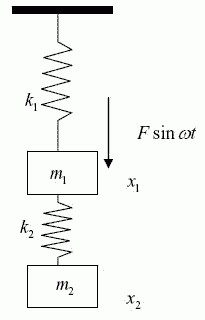
Proljetno njihalo

Drugi primjer slobodnih oscilacija harmonika su oscilacije tijela na izvoru. U stanju ravnoteže, opruga još nije deformirana, elastična sila ne djeluje na tijelo. Sila trenja između tijela i nosača je također nula. Sila privlačnosti se uravnotežuje snagom reakcije potpore. Ako se tijelo izvuče iz ravnoteže, pomiče se po osi OX na udaljenosti x = ± A , a zatim se oslobađa, klatno će slobodno oscilirati pod djelovanjem elastične sile, a slobodne oscilacije klatna pojavit će se prema zakonu x = Asinwt.

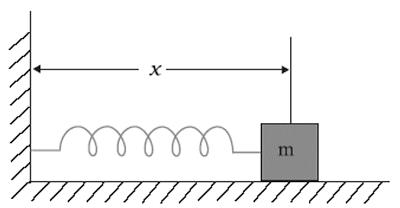
Period slobodnih oscilacija klatna na izvoru jednak je:

T = 2π / ω,

gdje je frekvencija cikličke oscilacije ω ² = k / m, k krutost opruge, m je masa tijela.

Kao što se može vidjeti iz formule, vrijeme i učestalost oscilacija opružnog njihala ne ovise o tome gravitacijsko ubrzanje i određuju ih samo masa suspendiranog tijela i krutost opruge.

Električne oscilacije u krugu

Električni krug u kojem su moguće slobodne elektromagnetske oscilacije naziva se oscilatorni krug. Sastoji se od kondenzatora s kapacitivnošću C, svitka s induktivitetom L i otpornika s otporom R (u stvarnom tehničkom krugu otpor svitka i spojnih vodiča imaju ulogu otpornika).

Ohmov zakon za zatvoreni krug, koji ne sadrži vanjski izvor struje iu kojem se javljaju slobodne elektromagnetske oscilacije, piše se u ovom obliku:

JR + U = - L (dJ / dt),

gdje je U = q / C napon na kondenzatoru, q je naboj kondenzatora, J = dq / dt je struja u krugu.

Slobodne oscilacije u krugu su harmonične, te se mijenjaju prema sljedećem zakonu:

q (t) = q ₀ cos (ωt + φ ₀ ).