Gaussova metoda za rješavanje matrica. Rješenje sustava linearnih jednadžbi Gaussovom metodom

Od početka XVI-XVIII stoljeća matematičari su počeli intenzivno proučavati funkcije zbog kojih se toliko promijenilo u našem životu. Računalna tehnologija bez tog znanja jednostavno ne bi postojala. Za rješavanje složenih problema, linearnih jednadžbi i funkcija stvoreni su različiti koncepti, teoreme i metode rješavanja. Jedna od takvih univerzalnih i racionalnih metoda i metoda za rješavanje linearnih jednadžbi i njihovih sustava bila je Gaussova metoda. Matrice, njihov rang, determinanta - sve se može izračunati bez upotrebe složenih operacija.

Što je slau

U matematici postoji koncept SLAE - sustava linearnih algebarskih jednadžbi. Kakva je ona? To je skup m jednadžbi s nepoznatim varijablama n nepoznatim, obično označenim kao x, y, z, ili x ₁ , x ₂ ... x _n, ili drugim simbolima. Rješavanje ovog sustava pomoću Gaussove metode znači pronaći sve nepoznate nepoznanice. Ako sustav ima isti broj nepoznanica i jednadžbi, tada se to naziva sustav n-tog reda.

Najpopularnije metode za rješavanje slaf

U obrazovnim ustanovama srednjeg obrazovanja proučavaju različite metode rješavanja takvih sustava. Najčešće su to jednostavne jednadžbe koje se sastoje od dvije nepoznanice, tako da svaka postojeća metoda pronalaženja odgovora na njih neće dugo trajati. To može biti metoda supstitucije, kada je druga izvedena iz jedne jednadžbe i zamijenjena izvornom. Ili metodu oduzimanja i zbrajanja. No Gaussova se metoda smatra najlakšom i univerzalnijom. To omogućuje rješavanje jednadžbi s bilo kojim brojem nepoznanica. Zašto se ova tehnika smatra racionalnom? Jednostavno je. Metoda matrice je dobra jer nema potrebe za ponovnim nepotrebnim prepisivanjem znakova nekoliko puta kao nepoznatim, dovoljno je izvršiti aritmetičke operacije na koeficijentima - i dobiti pouzdan rezultat.

Gdje se SLAE-i koriste u praksi

Rješenje SLAE-ova je sjecište crta na grafovima funkcija. U našem high-tech računalnom dobu, ljudi koji su usko povezani s razvojem igara i drugim programima trebaju znati kako riješiti takve sustave, što oni predstavljaju i kako provjeriti ispravnost dobivenih rezultata. Najčešće programeri razvijaju posebne računalne programe za linearnu algebru, a to uključuje sustav linearnih jednadžbi. Gaussova metoda omogućuje izračun svih postojećih rješenja. Koriste se i druge pojednostavljene formule i tehnike.

Kriterij kompatibilnosti SLAU

Takav se sustav može riješiti samo ako je kompatibilan. Radi jasnoće, predstavljamo SLAE kao Ax = b. Ima rješenje ako je rang (A) jednak rangu (A, b). U ovom slučaju (A, b) je matrica proširenog tipa, koja se može dobiti iz matrice A prepisivanjem s slobodnim članovima. Ispada da riješiti linearne jednadžbe Gaussova metoda je vrlo jednostavna.

Možda neka notacija nije posve jasna, pa trebate pogledati sve s primjerom. Pretpostavimo da postoji sustav: x + y = 1; 2x-3y = 6. Sastoji se od samo dvije jednadžbe, u kojima su 2 nepoznate. Sustav će imati rješenje samo ako je rang njegove matrice jednak rangu proširene matrice. Što je čin? To je broj neovisnih linija sustava. U našem slučaju rang matrice je 2. Matrica A će se sastojati od koeficijenata smještenih u blizini nepoznanica, a koeficijenti iza znaka "=" također se uklapaju u proširenu matricu.

Zašto SLAE može biti predstavljen u matričnom obliku

Na temelju kriterija kompatibilnosti prema dokazanom Kronecker-Capellijevom teoremu, sustav linearnih algebarskih jednadžbi može se prikazati u matričnom obliku. Pomoću Gaussove kaskadne metode možete riješiti matricu i dobiti jedini pouzdan odgovor na cijeli sustav. Ako je rang obične matrice jednak rangu njegove proširene matrice, ali je manji od broja nepoznanica, tada sustav ima beskonačan broj odgovora.

Matrične transformacije

Prije nego što pređemo na rješenje matrica, potrebno je znati koje se akcije mogu izvršiti na njihovim elementima. Postoji nekoliko osnovnih transformacija:

• Prepisivanjem sustava u matrični prikaz i implementacijom njegovog rješenja moguće je pomnožiti sve elemente retka istim koeficijentom.
• Kako bi matricu pretvorili u kanonski oblik, možete zamijeniti dva paralelna reda. Kanonska forma podrazumijeva da svi elementi matrice, koji se nalaze na glavnoj dijagonali, postaju jedinice, a preostali - nule.
• Odgovarajući elementi paralelnih redova matrice mogu se dodati jedan drugom.

Jordan-Gaussova metoda

Suština rješavanja sustava linearnih homogenih i nehomogenih jednadžbi Gaussovom metodom je postupno uklanjanje nepoznanica. Pretpostavimo da imamo sustav od dvije jednadžbe u kojima postoje dvije nepoznanice. Da biste ih pronašli, morate provjeriti kompatibilnost sustava. Jednadžba Gaussovom metodom riješena je vrlo jednostavno. Potrebno je ispisati koeficijente koji se nalaze u blizini svakog nepoznatog u matričnom prikazu. Da biste riješili sustav, trebat ćete ispisati proširenu matricu. Ako jedna od jednadžbi sadrži manji broj nepoznanica, tada je potrebno staviti "0" umjesto elementa koji nedostaje. Na matricu se primjenjuju sve poznate metode transformacije: množenje, dijeljenje brojem, dodavanje odgovarajućih elemenata redova jedan prema drugom i drugi. Ispada da je u svakom redu potrebno ostaviti jednu varijablu s vrijednošću "1", a ostatak dovesti do nultog oblika. Za točnije razumijevanje potrebno je razmotriti Gaussovu metodu s primjerima.

Jednostavan primjer 2x2 sustavnog rješenja.

Najprije uzmemo jednostavan sustav algebarskih jednadžbi u kojem će biti 2 nepoznanice.

Ponovo ga napišite u proširenu matricu.

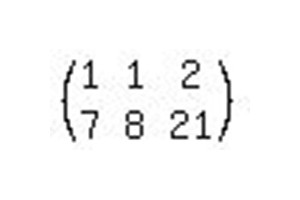
Da bi se riješio ovaj sustav linearnih jednadžbi, potrebno je izvršiti samo dvije operacije. Trebamo matricu dovesti u kanonski oblik tako da jedinice stoje uzduž glavne dijagonale. Dakle, prebacujući se iz matričnog pogleda natrag u sustav, dobivamo jednadžbe: 1x + 0y = b1 i 0x + 1y = b2, gdje su b1 i b2 rezultat odgovora u procesu rješavanja.

1. Prvi korak u rješavanju proširene matrice bio bi: prvi red mora biti pomnožen s -7 i odgovarajući elementi dodani drugom redu, respektivno, kako bi se riješili jedne nepoznate u drugoj jednadžbi.
2. Budući da rješenje jednadžbi Gaussovom metodom podrazumijeva redukciju matrice na kanonsku formu, tada je nužno izvršiti iste operacije s prvom jednadžbom i ukloniti drugu varijablu. Da bismo to učinili, oduzimamo drugu liniju od prve i dobijemo potreban odgovor - SLAU rješenje. Ili, kao što je prikazano na slici, drugi red se pomnoži s koeficijentom -1 i elementi drugog reda dodaju se prvom retku. To je ista stvar.

Kao što možete vidjeti, naš sustav se rješava metodom Jordan-Gauss. Prepisujemo ga u traženi oblik: x = -5, y = 7.

Primjer 3x3 SLAE otopine

Pretpostavimo da imamo složeniji sustav linearnih jednadžbi. Gaussova metoda omogućuje izračun odgovora čak i za naizgled zbunjujući sustav. Stoga, kako bismo dobili dublji uvid u metodu izračuna, možemo se pomaknuti na složeniji primjer s tri nepoznanice.

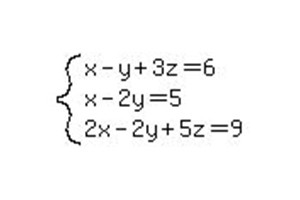
Kao iu prethodnom primjeru, prepisujemo sustav u obliku proširene matrice i počinjemo je reducirati na kanonski oblik.

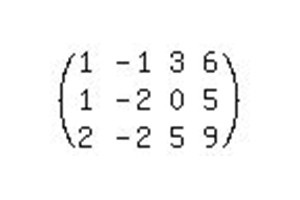
Da biste riješili ovaj sustav, morat ćete poduzeti mnogo više koraka nego u prethodnom primjeru.

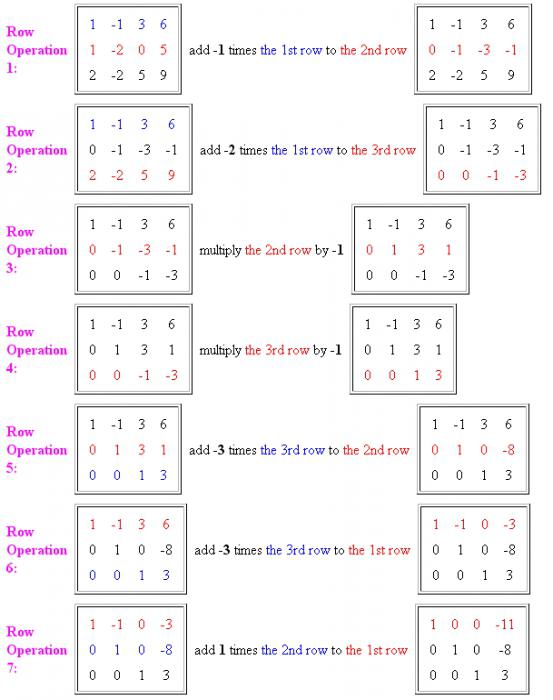
1. Prvo morate napraviti u prvom stupcu jedan element jedinice i preostale nule. Da biste to učinili, pomnožite prvu jednadžbu s -1 i dodajte drugu jednadžbu. Važno je zapamtiti da prvi redak prepisujemo u njegovom izvornom obliku, a drugi u modificiranom.
2. Zatim uklonite prvu prvu nepoznanicu iz treće jednadžbe. Da biste to učinili, elementi prvog reda pomnožite s -2 i dodajte ih u treći red. Sada se prvi i drugi red ponovno ispisuju u izvornom obliku, a treći - već s promjenama. Kao što se može vidjeti iz rezultata, dobili smo prvu jedinicu na početku glavne dijagonale matrice i preostale nule. Neke dodatne radnje i sustav jednadžbi koje koriste Gaussovu metodu bit će pouzdano riješeni.
3. Sada je potrebno izvršiti operacije na drugim elementima redaka. Treća i četvrta akcija mogu se kombinirati u jednu. Potrebno je podijeliti drugu i treću liniju za -1 kako bi se dijagonalno riješili negativnih jedinica. Treći redak već smo doveli do potrebnog oblika.
4. Slijedi drugi red u kanonski oblik. Da bismo to učinili, elemente trećeg retka pomnožimo s -3 i dodamo ih u drugi red matrice. Rezultat pokazuje da je drugi red također sveden na oblik koji nam je potreban. Ostaje još nekoliko operacija i uklanjanje koeficijenata nepoznanica iz prvog reda.
5. Da bi iz drugog elementa linije napravili 0, potrebno je treći redak pomnožiti s -3 i dodati ga prvom redu.
6. Sljedeći ključni korak bit će dodavanje u prvi red potrebnih elemenata drugog reda. Tako dobivamo kanonski oblik matrice i, shodno tome, odgovor.

Kao što možete vidjeti, rješenje jednadžbi Gaussovom metodom vrlo je jednostavno.

Primjer rješavanja 4x4 sustava jednadžbi

Neki složeniji sustavi jednadžbi mogu se riješiti Gaussovom metodom pomoću računalnih programa. U postojeće prazne ćelije potrebno je uvesti koeficijente s nepoznanicama, a sam program će korak po korak izračunati potreban rezultat, detaljno opisujući svaku radnju.

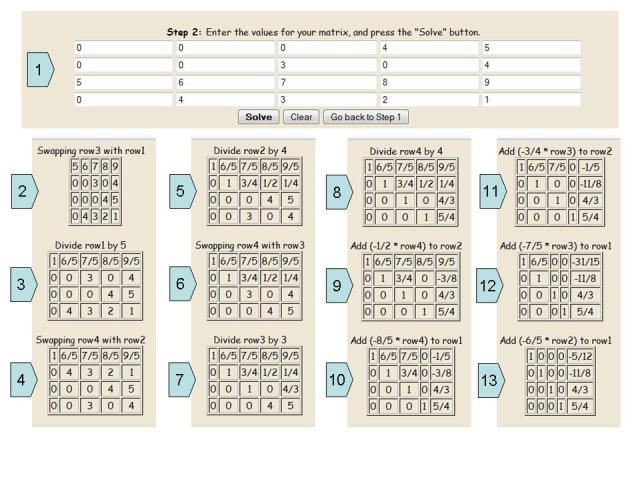
U nastavku slijedi korak po korak za rješavanje takvog primjera.

• U prvom koraku slobodni koeficijenti i brojevi s nepoznatim vrijednostima uklapaju se u prazne ćelije. Dakle, ispada ista proširena matrica, koju pišemo rukom.

• Zatim su sve linije obrnute tako da se jedinični elementi mogu izraziti duž glavne dijagonale.

• I sve potrebne aritmetičke operacije se izvode kako bi proširenu matricu doveli u kanonski oblik. Treba razumjeti da odgovor na sustav jednadžbi nije uvijek isti - oni su cijeli brojevi. Ponekad rješenje može biti iz djelomičnih brojeva.

Rješenje za provjeru valjanosti

Jordan-Gaussova metoda omogućuje provjeru ispravnosti rezultata. Da bi se utvrdilo jesu li koeficijenti ispravno izračunati, potrebno je samo nadomjestiti rezultat u izvornom sustavu jednadžbi. Lijeva strana jednadžbe mora odgovarati desnoj strani, koja je iza znaka jednakosti. Ako se odgovori ne podudaraju, tada morate ponovno izračunati sustav ili pokušati primijeniti na njega drugu metodu rješavanja SLAE-a koji vam je poznat, kao što je supstitucija ili oduzimanje i dodavanje po terminu. Uostalom, matematika je znanost koja ima veliki broj različitih tehnika rješavanja. Ali zapamtite: rezultat mora uvijek biti isti, bez obzira na metodu koju ste koristili.

Gaussova metoda: najčešće pogreške pri rješavanju SLAE

Kod rješavanja linearnih sustava jednadžbi najčešće se javljaju pogreške kao što su netočni prijenos koeficijenata na matrični oblik. Postoje sustavi u kojima su neke nepoznanice odsutne u jednoj od jednadžbi, a zatim, prenoseći podatke u proširenu matricu, one se mogu izgubiti. Kao rezultat, pri rješavanju ovog sustava, rezultat možda neće odgovarati stvarnom.

Još jedna od glavnih pogrešaka može biti pogrešno pisanje konačnog rezultata. Potrebno je jasno razumjeti da će prvi koeficijent odgovarati prvom nepoznatom iz sustava, drugom prema drugom i tako dalje.

Gaussova metoda detaljno opisuje rješenje linearnih jednadžbi. Zahvaljujući njemu, lako je obaviti potrebne operacije i pronaći pravi rezultat. Osim toga, to je univerzalni alat za pronalaženje pouzdanog odgovora na jednadžbe bilo koje složenosti. Možda se zato često koristi u rješavanju SLAE-a.