Kako pronaći opseg: kroz promjer i radijus. Terminologija, osnovne formule i značajke likova

Krug - zatvorena krivulja, čije su točke na istoj udaljenosti od središta. Ova brojka je ravna. Stoga, rješenje problema, pitanje koje je kako pronaći duljina opsega je dovoljno jednostavno. Sve dostupne metode, razmatramo u današnjem članku.

Opisi oblika

Osim prilično jednostavne deskriptivne definicije, postoje još tri matematičke karakteristike kruga, koje već već odgovaraju na pitanje kako pronaći duljinu kruga:

• Sastoji se od točaka A i B i svih drugih, iz kojih se AB može vidjeti pod pravim kutom. Promjer ove brojke jednak je duljini razmatranog segmenta.
• Uključuje samo takve točke X, da je omjer AX / BX konstantan i nije jednak jednom. Ako taj uvjet nije zadovoljen, onda to nije krug.
• Sastoji se od točaka za koje vrijedi svaka sljedeća jednakost: zbroj kvadrata udaljenosti do druge dvije je zadana vrijednost, koja je uvijek veća od polovice duljine segmenta između njih.

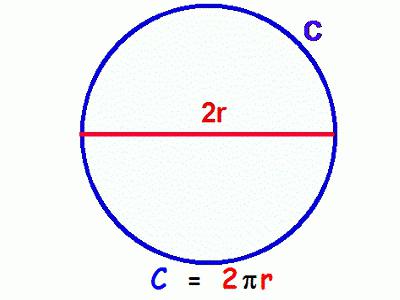
terminologija

Nisu svi u školi imali dobrog učitelja matematike. Stoga je odgovor na pitanje kako pronaći duljinu kruga kompliciran činjenicom da svi ne poznaju osnovne geometrijske koncepte. Radius - segment koji povezuje središte oblika s točkom na krivulji. Poseban slučaj u trigonometriji je jedinični krug. Akord je segment koji povezuje dvije točke krivulje. Na primjer, ova definicija spada u već razmatrane AB. Promjer je tetiva koja prolazi kroz središte. Broj π jednak je duljini jednog polukruga.

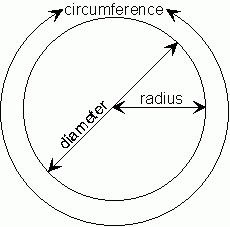
Osnovne formule

Iz definicija izravno slijedite geometrijske formule koje vam omogućuju izračunavanje glavnih značajki kruga:

1. Duljina je jednaka proizvodu broja π i promjera. Formula se obično piše na sljedeći način: C = π * D.
2. Polumjer je pola promjera. Također se može izračunati izračunavanjem kvocijenta od dijeljenja opsega dvostrukim brojem π. Formula izgleda ovako: R = C / (2 * π) = D / 2.
3. Promjer je jednak kvocijentu dijeljenja opsega s π ili dvostrukim polumjerom. Formula je vrlo jednostavna i izgleda ovako: D = C / π = 2 * R.
4. Područje kruga jednako je proizvodu broja π i kvadratu radijusa. Slično tome, u ovoj formuli možete koristiti promjer. U ovom slučaju, područje će biti jednako kvocijentu dijeljenja proizvoda broja π i kvadrata promjera za četiri. Formula se može napisati na sljedeći način: S = π * R ² = π * D 2/4.

Kako pronaći opseg promjera

Radi jednostavnosti objašnjenja, odredimo karakteristike potrebne za izračun. Neka je C željena dužina, D promjer, a broj π približno jednak 3.14. Ako imamo samo jednu poznatu količinu, onda se problem može smatrati riješenim. Zašto je to potrebno u životu? Pretpostavimo da smo odlučili priložiti okruglu ogradu od bazena. Kako izračunati potreban broj stupaca? I ovdje dolazi do spašavanja sposobnost, kako izračunati duljinu kruga. Formula je sljedeća: C = π D. U našem primjeru, promjer se određuje na temelju radijusa bazena i potrebne udaljenosti od ograde. Pretpostavimo, na primjer, da je naš umjetni akumulacijski bazen širok 20 metara, a stupove ćemo postaviti na udaljenosti od deset metara od njega. Promjer dobivenog kruga je 20 + 10 * 2 = 40 m. Duljina - 3,14 * 40 = 125,6 metara. Trebat će nam 25 stupaca, ako je razmak između njih oko 5 m.

Duljina kroz radijus

Kao i uvijek, počnimo s dodjeljivanjem slova krugu. Zapravo, one su univerzalne, tako da matematičari iz različitih zemalja ne moraju poznavati jezik jedni drugih. Pretpostavimo da je C duljina kruga, r je njegov radijus, a π približno je jednak 3,14. Formula u ovom slučaju izgleda ovako: C = 2 * π * r. Očito, ovo je apsolutno ispravna jednakost. Kao što smo već razumjeli promjer kruga jednaka dvostrukom radijusu, pa ova formula izgleda ovako. U životu, ova metoda također može biti vrlo korisna. Na primjer, pečemo kolač u posebnom kliznom obliku. Kako se ne bi zaprljali, treba nam dekorativni omot. Ali kako izrezati krug prave veličine. Ovdje spašava matematika. Oni koji znaju otkriti duljinu kruga odmah će reći da trebate pomnožiti broj π dvostrukim radijusom forme. Ako je njegov radijus 25 cm, tada će duljina biti 157 centimetara.

Primjeri zadataka

Već smo pregledali nekoliko praktičnih slučajeva znanja stečenog o tome kako saznati duljinu kruga. No često se ne bavimo njima, već stvarnim matematičkim problemima koji su sadržani u udžbeniku. Uostalom, za njih, učitelj stavlja bodove! Razmotrimo stoga problem povećane složenosti. Pretpostavimo da je opseg 26 cm. Kako pronaći radijus takve figure?

Primjer rješenja

Za početak, zapisujemo što nam je dano: C = 26 cm, π = 3.14. Također podsjetite formulu: C = 2 * π * R. Iz njega možete izvaditi radijus kruga. Dakle, R = C / 2 / π. Sada prijeđite na izravni izračun. Prvo podijelite duljinu za dva. Dobivamo 13. Sada moramo podijeliti s vrijednošću broja π: 13 / 3,14 = 4,14 cm Važno je ne zaboraviti ispravno zapisati odgovor, odnosno mjernim jedinicama, inače se gubi cjelokupno praktično značenje tih zadataka. Osim toga, za takvu nepažnju možete dobiti ocjenu od jedne točke niže. Bez obzira na to koliko je neugodno, morate se nositi s takvim stanjem stvari.

Zvijer nije tako strašna kao što je slikana

Tako smo shvatili takav naizgled težak zadatak. Kako se ispostavilo, samo trebate razumjeti značenje pojmova i zapamtiti nekoliko jednostavnih formula. Matematika nije tako zastrašujuća, samo treba malo truda. Tako vas geometrija čeka!