Kako pronaći volumen kocke: opcije za probleme i njihovo rješenje
Moderne tehnologije stvaraju nevjerojatne računalne programe. Oni vam omogućuju da vidite tijelo u volumenu i okrenete ih u različitim smjerovima kako biste dobili bolji izgled. Čovjekova mašta nije uvijek sposobna za to. Malo tko može jasno predstaviti temu i vidjeti je. No, takva se vještina može pokušati formirati pri rješavanju problema u geometriji. Na primjer, oni koji govore o tome kako pronaći volumen kocke. To je izvrsna praksa za razvoj prostorne imaginacije.
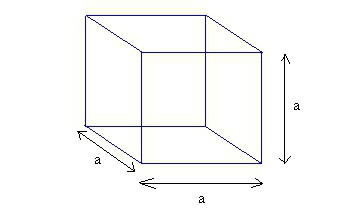
Kocka ili paralelopiped?
Ovo je ne-prazno pitanje. Zato što je klasifikacija važna. Uostalom, kocka je poseban oblik pravokutnog paralelepipeda.
Potonji je lik u kojem ima 6 lica, a svi su pravokutnici. Kutovi na kojima se svi rubovi sijeku, 90º. Prema tome, ako ta lica postanu kvadrati, tada će se cijeli lik pretvoriti u kocku.

U pravokutnom paralelopipedu, sve linearne dimenzije, tj. Visina, dužina i širina, mogu se značajno razlikovati. U kocki su uvijek jednake jedna drugoj. To je njezin zaštitni znak. Stoga, u zadacima koji zahtijevaju pronalaženje volumena kocke, svakako se uzima u obzir razmatrani trenutak. Usput, to uvelike pojednostavljuje sve matematičke zapise i izračune.
Konvencije u formulama i problemima
Bez ove stavke bit će teško razumjeti kako su formule napisane. Ono što se podrazumijeva pod svakim slovom i simbolom, potiče sljedeću tablicu.
| simbol | Naziv stavke |
| i | oblik rebra |
| d | dijagonalno lice |
| D | dijagonalna kocka |
| zajednički geometrijski simboli | područje |
| volumen |
Kako pronaći elemente kocke na svojoj strani?
Budući da je lice slike kvadrat, njegovo područje određeno je formulom br. 1, u kojoj se poznata vrijednost mora kvadrirati:
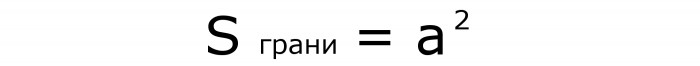
I dijagonala bilo kojeg lica izračunava se pomoću formule br. 2, u kojoj se strana množi s korijenom od 2:
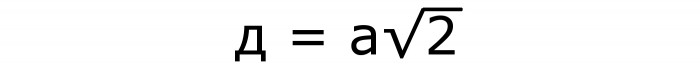
Prethodna formula dobiva se iz Pitagorina teorema. To je lako razumjeti ako vidite da je dijagonala lica hipotenuza pravokutni trokut. I strane trga postaju njezine noge.
Za određivanje dijagonale kocke potrebna je sljedeća formula br. 3 koja sadrži poznatu stranu i kvadratni korijen od 3:
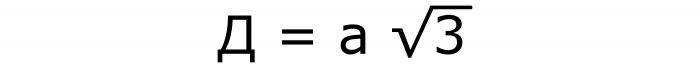
Također se dobiva iz Pitagoreanskog teorema. Samo kao hipotenuza djeluje željena dijagonala. Strana trga i dijagonala postaju noge.
Ponekad morate znati formulu za izračun površine bočne površine ove figure. U njemu se kvadrat na strani množi sa 4. Ovdje je (br. 4):
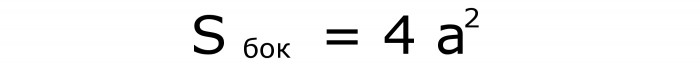
Lako je razumjeti kako ova formula funkcionira. Postoje 4 bočna lica - 4. To znači da je njihova ukupna površina četverostruka vrijednost površine jednog kvadrata.
Ako trebate odrediti površinu cijele površine , tada upotrijebite ovaj zapis u kojem se trguje kvadratom rebra (formula br. 5):
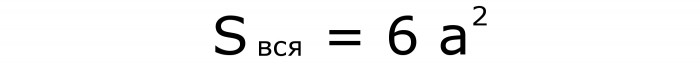
Dobiva se slično prethodnoj formuli, samo je broj kvadrata povećan na 6.
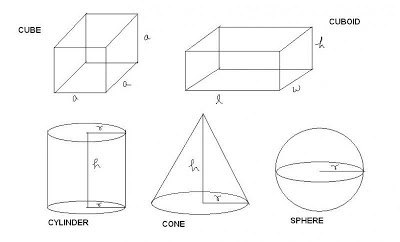
Što je volumen?
Jednostavno rečeno, ovo je mjesto koje uzima svako tijelo u prostoru. Svaki je objekt u prostoru ograničen površinama. Može ih biti nekoliko, ali može biti slučajeva kada je samo jedan. Na primjer, ako je tijelo lopta. Ali te su površine nužno zatvorene. Prostor koji geometrijsko tijelo zauzima bit će njegov kapacitet ili volumen.
Jedinice volumena
Kad je riječ o krutim tvarima, jedinice volumena uvijek će biti kubične vrijednosti. Na primjer, metar, centimetar ili kilometar u kocki. Za tekućine se koriste litri, izraženi u kubnim decimetrima. Ali ako zauzimaju vrlo velike količine, mjere se i u kubnim metrima. Na primjer, uzimajući u obzir potrošnju vode u stanu, smatra se da je u m 3 . Tako se ispostavilo da je to praktičnije i lakše u brojčanom smislu.
Metoda 1: pronađite volumen kocke, ako je poznata strana
To je najjednostavniji način da vam kaže kako pronaći volumen kocke. To je jednostavno podizanje vrijednosti stranke na treći stupanj. Drugim riječima, trebate sami umnožiti stranu tri puta. Po analogiji s proizvoljnim pravokutnim paralelepipedom, kada je bilo potrebno množiti sve njegove linearne dimenzije. Formula će biti napisana na sljedeći način (# 6):
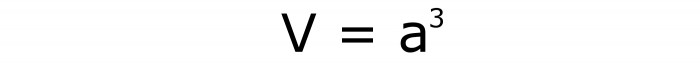
Metoda 2: cijela površina je poznata
U tom slučaju, morate podijeliti poznatu vrijednost sa 6. Iz internog odgovora, izvadite kvadratni korijen i podignite broj na kocku. Ako napišemo ovu formulu, dobit ćemo sljedeće (# 7):
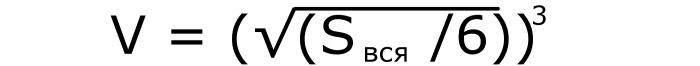
Metoda 3: s dijagonalnom stranom kocke
Da biste saznali kako izračunati volumen kocke, u ovom slučaju, morate izvršiti sljedeće korake. Prvo, izgradite poznatu vrijednost u kocku, a zatim je pomnožite s kvadratnim korijenom od 2 i podijelite s 4. Formula za ovaj problem (br. 8):
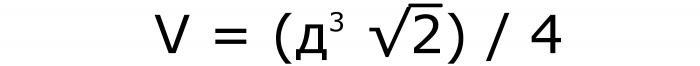
Ta se jednadžba dobiva na ovaj način: poznata dijagonala mora biti podijeljena korijenom dvaju. Zatim izgradite broj do trećeg stupnja. Nakon provedenih transformacija, u numeratoru se dobiva kocka dijagonale, a 2 in2 u nazivniku. Matematika zahtijeva da ne postoji iracionalan broj ispod crte. Stoga ga se oslobađaju množenjem s .2. Tada se ator2 pojavljuje u brojniku, a 4 se dobiva u nazivniku.
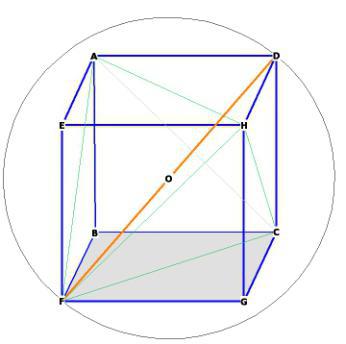
Metoda 4: Kocka dijagonala
Formula koja vam kaže kako pronaći volumen kocke sadržavat će akcije: kvadriranje dijagonale, množenje za korijen od 3, i dijeljenje s samo 9. To će biti napisano ovako (br. 9):
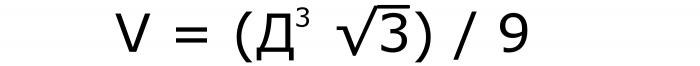
Slično prethodnoj formuli, u ovom zapisu dijagonala se prvo dijeli na korijen od tri i podiže na kocku. Nakon transformacija u nazivniku pojavljuje se i iracionalnost, iz koje je potrebno otići. Tako se vrijednost appears3 pojavljuje u brojniku, a ispod crte - 9.
Primjeri zadataka
Zadatak jedan. Dobivena je kocka s rubom od 12 cm, izračunati volumen i izraziti odgovor u četvornim metrima.
U ovom zadatku bit će teže prevesti odgovor u druge jedinice nego odlučiti kako pronaći volumen kocke. Da biste dovršili prvi dio zadatka, trebat će vam formula napisana pod brojem 6. Nakon što je broj 12 ugrađen u kocku, odgovor će biti 1728 cm3. Sada se moramo sjetiti kako ih prevesti u kubične metara. U tu svrhu, odgovor mora biti podijeljen na 100 tri puta. Stotinjak je došlo od činjenice da je stotinjak centimetara na jednom metru. A podjela se izvodi tri puta, jer su jedinice u zadatku kubične. Dakle, 1728 podijeljeno sa 100 dat će 17.28. Nakon druge podjele bit će 0.1728. Treći korak će dati odgovor 0,001728 m 3 . To je odgovor na problem: volumen kocke je 0,001728 m 3 .
Zadatak dva. Postoji kocka s cijelom površinom površine 600 dm 2 . Pronađite volumen oblika i izrazite ga u kubnim metrima.
Da biste odgovorili na pitanje o ovom zadatku, trebat će vam formula broj 7. Prvo djelovanje je poznati broj podijeljen sa 6. Odgovor donosi 100. Lako je izvući iz njega kvadratni korijen, to će biti 10. Sada trebate izgraditi prvih deset u kocki. Tako se ispostavlja da je željena vrijednost jednaka 1000 dm 3 . Ostaje pretvoriti ga u m 3 . Kao iu prethodnom zadatku, podjela će se izvršiti tri puta, samo će djelitelj biti 10. Jer ima deset decimetara u jednom metru. Nakon podjele, odgovor je 1 m 3 . Odgovor: glasnoća je 1 m 3 .
Treći zadatak. S obzirom na kocku s dijagonalnom duljinom lica od √2 mm. Potrebno je izračunati volumen.
Osma formula pomoći će u pronalaženju odgovora u ovom problemu. Prva stvar koju trebate napraviti je kocka poznate vrijednosti. Kvadratni korijen od 2 u trećem stupnju će dati vrijednost 2√2. Nakon množenja s ,2, dobivamo broj 4. Posljednja akcija je podjela na 4. Odgovor: volumen kocke je 1 mm3.
Četvrti zadatak. Poznato je da je dijagonala kocke 3 m. Potrebno je izračunati njegov volumen.
Odgovor na ovaj problem lako će se naći pomoću formule broj 9. Vrijednost dana u stanju mora biti podignuta na kocku. Ispada 27. Nakon što ga podijelimo s 9, odgovor će biti 3. I posljednja akcija treba pomnožiti s kvadratnim korijenom od 3. Odgovor problema će biti 3√3 m 3 .