Kinetička energija - energija gibanja tijela
Potencijalna i kinetička energija dopuštaju nam da karakteriziramo stanje bilo kojeg tijela. Ako se prva koristi u sustavima interakcijskih objekata, onda je ona povezana s njihovim kretanjem. Ove se vrste energije, u pravilu, razmatraju kada je sila koja povezuje tijela neovisna o putanji kretanja. U ovom slučaju važni su samo početni i završni položaji.
Opće informacije i koncepti
Kinetička energija sustava jedna je od njegovih najvažnijih karakteristika. Fizičari razlikuju dvije vrste takve energije ovisno o vrsti gibanja:
• progresivno;
• rotacija.
Kinetička energija ( Ek ) je razlika između ukupne energije sustava i preostale energije. Na temelju toga možemo reći da je to zbog kretanja sustava. Tijelo ga ima samo kad se kreće. U mirovanju, objekt je nula. Kinetička energija bilo kojeg tijela ovisi isključivo o brzini kretanja i njihovim masama. Ukupna energija sustava izravno ovisi o brzini njegovih objekata i udaljenosti između njih.
Osnovne formule
U slučaju kada bilo koja sila (F) djeluje na tijelo koje je u mirovanju na takav način da dolazi u pokret, možemo govoriti o obavljanju posla dA. Vrijednost ove energije dE bit će veća, više će se raditi. U ovom slučaju vrijedi sljedeća jednakost: dA = dE.
S obzirom na put kojim prolazi tijelo (dR) i njegova brzina (dU), možete koristiti 2 Newtonov zakon, na temelju kojeg: F = (dU / dE) * m.
Navedeni zakon se koristi samo kada postoji inertni referentni sustav. Postoji još jedna važna nijansa koja se uzima u obzir u izračunima. Na vrijednost energije utječe izbor sustava. Prema SI sustavu, on se mjeri u džulima (J). Kinetičku energiju tijela karakterizira masa m, kao i brzina kretanja υ. U ovom slučaju to će biti: E k = ((υ * υ) * m) / 2.
Na temelju gornje formule možemo zaključiti da je kinetička energija određena masom i brzinom. Drugim riječima, to je funkcija pokreta tijela.
Energija u mehaničkom sustavu
 Kinetička energija je mehanička energija sustav. To ovisi o brzini njegovih točaka. S obzirom na energiju materijalna točka predstavlja sljedeću formulu: E = 1 / 2mυ 2, gdje je m masa točke, a υ brzina.
Kinetička energija je mehanička energija sustav. To ovisi o brzini njegovih točaka. S obzirom na energiju materijalna točka predstavlja sljedeću formulu: E = 1 / 2mυ 2, gdje je m masa točke, a υ brzina.
Kinetička energija mehaničkog sustava je aritmetička suma istih energija svih njezinih točaka. Također se može izraziti sljedećom formulom: E k = 1 / 2Mυ c2 + Ec, gdje je υc brzina središta mase, M je masa sustava, Ec je kinetička energija sustava pri kretanju oko središta mase.
Čvrsta energija
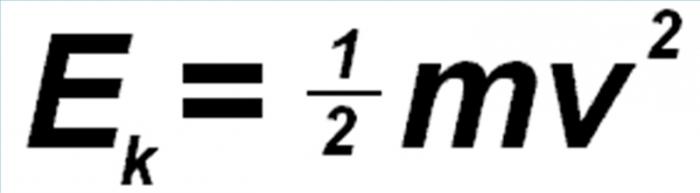 Kinetička energija tijela, koja se kreće progresivno, određena je istom energijom točke s masom jednakom masi cijelog tijela. Za izračun pokazatelja prilikom kretanja primjenjuju se složenije formule. Promjena te energije sustava u trenutku njezina kretanja iz jednog položaja u drugo događa se pod utjecajem primijenjenih unutarnjih i vanjskih sila. To je jednako zbroju rada Aue i A'u tih sila tijekom tog kretanja: E2 - E1 = Au Aue + Au A'u.
Kinetička energija tijela, koja se kreće progresivno, određena je istom energijom točke s masom jednakom masi cijelog tijela. Za izračun pokazatelja prilikom kretanja primjenjuju se složenije formule. Promjena te energije sustava u trenutku njezina kretanja iz jednog položaja u drugo događa se pod utjecajem primijenjenih unutarnjih i vanjskih sila. To je jednako zbroju rada Aue i A'u tih sila tijekom tog kretanja: E2 - E1 = Au Aue + Au A'u.
Ta jednakost odražava teorem o promjeni kinetičke energije. Uz njegovu pomoć rješavaju se najrazličitiji problemi mehanike. Bez ove formule nemoguće je riješiti niz važnih zadataka.
Kinetička energija pri velikim brzinama
Ako je brzina tijela blizu brzine svjetlosti, kinetička energija materijalne točke može se izračunati sljedećom formulom:
E = m0c2 / -1-υ2 / c2 - m0c2,
gdje je c brzina svjetlosti u vakuumu, m0 je masa točke, m0c2 je energija točke. Na maloj brzini (υ Za vrijeme rotacije tijela oko osi, svaki njezin elementarni volumen mase (mi) opisuje krug radijusa ri. U ovom trenutku volumen ima linearnu brzinu υi. Budući da se smatra čvrsta tvar, kutna brzina rotacija svih volumena bit će ista: ω = υ1 / r1 = υ2 / r2 = ... = υn / rn (1). Kinetička energija rotacije krutine je zbroj svih istih energija njezinih elementarnih volumena: E = m1υ1 2/2 + miυi 2/2 + ... + mnυn 2/2 (2). Kod izraza (1) dobivamo formulu: E = Jz ω 2/2, gdje je Jz trenutak inercije tijela oko Z osi. Kada se uspoređuju sve formule, postaje jasno da je trenutak inercije mjera tjelesne inercije tijekom rotacijsko gibanje. Formula (2) je pogodna za objekte koji rotiraju oko fiksne osi. Kinetička energija tijela koje se kreće niz ravninu sastoji se od energije rotacije i translacijskog gibanja: E = mυc2 / 2 + Jz ω 2/2, gdje je m masa pokretnog tijela, Jz je trenutak inercije tijela oko osi, υc je brzina centra mase, ω je kutna brzina. Promjena vrijednosti kinetičke energije usko je povezana s potencijalom. Suština ovog fenomena može se razumjeti kroz zakon očuvanja energije u sustavu. Zbroj E + dP tijekom kretanja tijela uvijek će biti isti. Promjena vrijednosti E uvijek se javlja istovremeno s promjenom dP. Dakle, oni se transformiraju, kao da teče jedno u drugo. Takav fenomen može se naći u gotovo svim mehaničkim sustavima. Za izračun energetske vrijednosti bira se proizvoljni trenutak (smatra se početnim) i referentni sustav. Točnu količinu potencijalne energije moguće je odrediti samo u zoni utjecaja sila koje ne ovise o putanji tijela prilikom izrade. U fizici se te sile nazivaju konzervativne. Oni imaju stalnu vezu s zakonom o očuvanju energije. Ako je vanjski utjecaj minimalan ili sveden na nulu, sustav koji se istražuje uvijek će biti u stanju u kojem će njegova potencijalna energija također težiti nuli. Primjerice, bacena lopta će dosegnuti granicu te energije u gornjoj točki putanje i u istom trenutku će početi padati. U ovom trenutku, akumulirana energija u letu pretvara se u pokret (izvedeni rad). Za potencijalnu energiju, u svakom slučaju, postoji interakcija barem dvaju tijela (u primjeru s loptom, gravitacija planeta utječe na nju). Kinetička energija se može izračunati pojedinačno za svako pomično tijelo. Potencijalna i kinetička energija mijenja se isključivo u interakciji tijela, kada sila koja djeluje na tijelo obavlja posao, čija se vrijednost razlikuje od nule. U zatvorenom sustavu rad sile sile ili elastičnosti jednak je promjeni potencijalne energije objekata sa znakom "-": A = - (Ep2 - Ep1). Rad sile ili elastičnosti jednak je promjeni energije: A = Ek2 - Ek1. Iz usporedbe obje jednadžbe jasno je da je promjena energije objekata u zatvorenom sustavu jednaka promjeni potencijalne energije i suprotna je predznaku: Ek2 - Ek1 = - (Ep2 - Ep1), ili na drugi način: Ek1 + Ep1 = Ek2 + Ep2. Iz ove jednakosti jasno je da zbroj tih dviju energija tijela u zatvorenom mehaničkom sustavu i međudjelujućim silama elastičnosti i agresivnosti uvijek ostaje konstantan. Na temelju navedenog može se zaključiti da u procesu proučavanja mehaničkog sustava treba razmotriti interakciju potencijalne i kinetičke energije. 
Rotacijska energija sustava
Planarni pokret tijela

Promjena energije u mehaničkom sustavu
Energetska povezanost
Potencijalne i kinetičke energije usko su povezane. Njihov se iznos može prikazati kao ukupna energija sustava. Na molekularnoj razini to jest unutarnja energija Tijelo. Prisutna je stalno, sve dok postoji barem neka interakcija između tijela i toplinskog gibanja. Izbor referentnog sustava
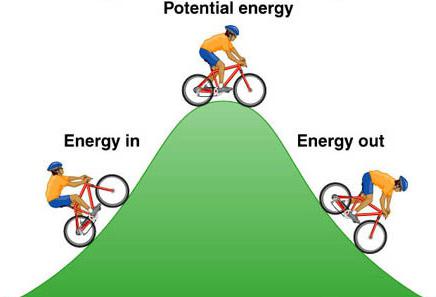
Suština razlike između potencijalne i kinetičke energije
Povezivanje različitih energija