Paralaksa je ono što je?

Kosmos je jedan od najtajanstvenijih koncepata u svijetu. Ako gledate u nebo noću, možete vidjeti bezbroj zvijezda. Da, vjerojatno, svatko od nas je čuo da u svemiru ima više zvijezda od zrnaca pijeska u Sahari. A znanstvenici iz davnih vremena pružali su se na noćno nebo, pokušavajući riješiti zagonetke skrivene iza te crne praznine. Od davnina imaju poboljšane metode mjerenja udaljenosti prostora i svojstava zvijezde (temperatura, gustoća, brzina vrtnje). U ovom članku ćemo govoriti o tome što je paralaksa zvijezda i kako se ona koristi u astronomiji i astrofizici.

Fenomen paralakse usko je povezan s geometrijom, ali prije nego što razmotrimo geometrijske zakone koji leže u pozadini ove pojave, uronit ćemo u povijest astronomije i ispitati tko i kada je otkrio ovo svojstvo gibanja zvijezda i prvo ga primijenio u praksi.

Povijest

Paralaksa kao fenomen promjene položaja zvijezda ovisno o mjestu promatrača poznata je već dugo vremena. Više o tome Galileo Galileo pisao je u dalekom srednjem vijeku. On je samo pretpostavio da ako je moguće primijetiti promjenu paralakse za udaljene zvijezde, to bi bio dokaz Zemlja se vrti oko sunca, a ne obrnuto. I to je istina. Međutim, Galileo to nije mogao dokazati zbog nedovoljne osjetljivosti tadašnje opreme.

Bliže našim danima, 1837. godine, Vasily Yakovlevich Struve proveo je niz eksperimenata kako bi izmjerio godišnju paralaksu za zvijezdu Vegu, koja se nalazi u zviježđu Lyra. Kasnije su se ta mjerenja smatrala nepouzdanim kada je, u godini nakon objavljivanja Struvea, 1838., Friedrich Wilhelm Bessel izmjerio godišnju paralaksu za zvijezdu Cygnus. Stoga, bez obzira koliko to bilo tužno, prioritet otvaranja jednogodišnje paralakse još uvijek pripada Besselu.

Danas se kao glavna koristi paralaksa metoda mjerenja udaljenosti do zvijezda i dovoljno preciznom mjernom opremom daje rezultate s minimalnom pogreškom.

Trebali bismo prijeći na geometriju prije nego što izravno razmotrimo što je paralaksa. I za početak, prisjetimo se samih osnove ovog zanimljivog, iako nezasićenog od mnogih znanosti.

Osnove geometrije

Dakle, ono što trebamo znati iz geometrije da bismo razumjeli fenomen paralakse je kako su kutovi između strana trokuta i njihove duljine povezani.

Za početak zamislite trokut. Ima tri ravne linije i tri kuta. I za svaki drugi trokut - vlastiti kutovi i duljine stranica. Nemoguće je promijeniti veličinu jedne ili dvije strane trokuta s konstantnim vrijednostima kutova između njih, to je jedna od temeljnih istina geometrije.

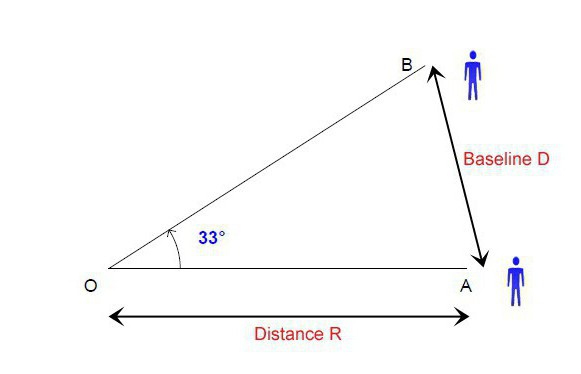
Zamislite da se susrećemo sa zadatkom pronalaženja vrijednosti duljina dviju strana, ako znamo samo duljinu baze i veličinu uglova koji se nalaze uz njega. To je moguće uz pomoć jedne matematičke formule koja povezuje vrijednosti duljina stranica i vrijednosti kutova koji leže nasuprot njima. Dakle, zamislite da imamo tri vrha (možete uzeti olovku i nacrtati ih) koji čine trokut: A, B, C. Oni tvore tri strane: AB, BC, CA. Nasuprot svakom od njih leži kut: kut BCA nasuprot AB, kut BAC nasuprot BC, kut ABC nasuprot CA.

Formula koja povezuje svih ovih šest količina zajedno izgleda ovako:

AB / sin (BCA) = BC / sin (BAC) = CA / sin (ABC).

Kao što možemo vidjeti, sve nije sasvim jednostavno. Odnekud imamo sinus od kutova. Ali kako ćemo pronaći taj sinus? O tome ćemo reći u nastavku.

Osnove trigonometrije

Sinus je trigonometrijska funkcija koja određuje Y koordinatu kuta na koordinatnoj ravnini. Da bi se to jasno pokazalo, obično crtaju koordinatnu ravninu s dvije osi - OX i OY - i označavaju točke 1 i -1 na svakoj od njih. Te se točke nalaze na istoj udaljenosti od središta ravnine, pa se kroz njih može izvući krug. Dakle, imamo takozvani jedinstveni krug. Sada ćemo konstruirati neki segment s početkom na početku koordinata, a kraj u nekoj točki našeg kruga. Kraj segmenta koji leži na krugu ima određene koordinate na osi OX i OY. Vrijednosti tih koordinata će biti kosinus i sinus.

Saznali smo što je sinus i kako ga možete pronaći. No, u stvari, ova metoda je čisto grafička i stvorena je bolje razumjeti samu bit trigonometrijskih funkcija. Može biti djelotvorna za kutove koji nemaju beskonačne racionalne vrijednosti kosinusa i sinusa. Za potonje je učinkovitija druga metoda, koja se temelji na korištenju derivata i binomnih izračuna. To se zove Taylorova serija. Ovu metodu nećemo razmatrati jer je za izračun na umu prilično komplicirana. Uostalom, brzi rad je posao za računala koja su za to namijenjena. Taylorova serija koristi se u kalkulatorima za izračunavanje mnogih funkcija, uključujući sinus, kosinus, logaritam i tako dalje.

Sve je to vrlo zanimljivo i zarazno, ali vrijeme je da krenemo dalje i vratimo se tamo gdje smo završili: na zadatku izračunavanja vrijednosti nepoznatih strana trokuta.

Strane trokuta

Dakle, vratimo se na naš problem: znamo dva kuta i stranu trokuta, kojima su ti kutovi susjedni. Moramo znati samo jedan kut i dvije strane. Čini se da je pronalaženje kuta najlakši: zbroj sva tri kuta trokuta je 180 stupnjeva, što znači da možete lako pronaći treći kut oduzimanjem vrijednosti dvaju poznatih kutova od 180 stupnjeva. I znajući vrijednosti sva tri kuta i jednu od strana, možemo pronaći duljine dvije druge strane. Možete ga sami provjeriti na primjeru bilo kojeg trokuta.

A sada napokon govorimo o paralaksi kao o načinu mjerenja udaljenosti između zvijezda.

paralaksa

To je, kao što smo već otkrili, jedna od najjednostavnijih i najučinkovitijih metoda za mjerenje međuzvjezdanih udaljenosti. Paralaksa se temelji na promjeni položaja zvijezde ovisno o njezinoj udaljenosti. Primjerice, mjerenjem kuta prividne pozicije zvijezde u jednoj točki orbite, a zatim izravno u suprotnom smjeru, dobivamo trokut u kojem su poznate duljine jedne strane (udaljenost između suprotnih točaka orbite) i dva kuta. Odavde ćemo moći pronaći dvije preostale strane, od kojih je svaka jednaka udaljenosti od zvijezde do našeg planeta na različitim točkama njegove orbite. To je metoda kojom se može izračunati paralaksa zvijezda. I ne samo zvijezde. Paralaksa, čiji je učinak zapravo vrlo jednostavan, unatoč tome, koristi se u mnogim njegovim varijacijama u potpuno različitim područjima.

U sljedećim odjeljcima pobliže ćemo razmotriti opseg paralakse.

prostor

O tome smo više puta razgovarali, jer je paralaksa izniman izum astronoma, dizajniran za mjerenje udaljenosti do zvijezda i drugih svemirskih objekata. Međutim, to nije tako jednostavno. Naposljetku, paralaksa je metoda koja ima svoje varijacije. Na primjer, razlikuju se dnevne, godišnje i prastare paralakse. Može se pretpostaviti da se svi razlikuju u intervalu vremena koji prolazi između mjernih koraka. Ne može se reći da povećanje vremenskog intervala povećava točnost mjerenja, jer su ciljevi svakog tipa ove metode različiti, a točnost mjerenja ovisi samo o osjetljivosti opreme i odabranoj udaljenosti.

Dnevna paralaksa

Dnevna paralaksa, udaljenost kojom se određuje kut između linija koje idu do zvijezde iz dvije različite točke: središte Zemlje i odabrana točka na Zemlji. Budući da znamo radijus našeg planeta, nije teško, koristeći kutnu paralaksu, izračunati udaljenost do zvijezde, koristeći matematičku metodu koju smo ranije opisali. U osnovi, dnevna paralaksa se koristi za mjerenje blizu objekata, kao što je planeti, patuljasti planeti ili asteroida. Za veće korištenje sljedeće metode.

Jedna godina paralakse

Jednogodišnja paralaksa je još uvijek ista metoda mjerenja udaljenosti s jedinom razlikom što se fokusira na mjerenje udaljenosti do zvijezda. To je upravo slučaj paralakse koji smo razmatrali u gornjem primjeru. Paralaksa, određivanje udaljenosti do zvijezde čija pomoć može biti vrlo točna, trebala bi imati jednu važnu značajku: udaljenost od koje se mjeri paralaksa treba biti veća, to bolje. Jednogodišnja paralaksa zadovoljava ovaj uvjet: nakon svega, udaljenost između ekstremnih točaka orbite je prilično velika.

Paralaksa, primjeri metoda koje smo razmatrali, svakako je važan dio astronomije i služi kao nezamjenjiv alat u mjerenju udaljenosti do zvijezda. Zapravo, danas se koristi samo jednogodišnja paralaksa, jer se dnevna može zamijeniti naprednijom i bržom eholokacijom.

Samo naprijed. Paralaksa je još uvijek optički fenomen i bilo bi čudno da se njezina svojstva koriste samo u astronomiji. Postoji još jedno područje primjene ovog učinka.

foto

Možda najpoznatiji tip fotografske paralakse može biti binokularna paralaksa. Vjerojatno ste to i sami primijetili. Ako prstom dovedete oči i zatvorite svako oko, primijetit ćete da se mijenja kut gledanja objekta. Isto se događa i pri snimanju blizu objekata. U objektivu vidimo sliku iz jednog kuta, ali zapravo će fotografija izaći s malo drugačijim kutem, jer postoji razlika u udaljenosti između objektiva i tražila (rupa kroz koju gledamo fotografiju).

Prije nego što završimo ovaj članak - nekoliko riječi o tome kako takva pojava kao što je optička paralaksa može biti korisna i zašto biste trebali saznati više o tome.

Zašto je to zanimljivo?

Za početak, paralaksa je jedinstveni fizički fenomen koji nam omogućuje da naučimo mnogo o svijetu oko nas, pa čak io onome što je u stotinama svjetlosnih godina od njega: nakon svega, uz pomoć ovog fenomena moguće je izračunati veličine zvijezda.

Kao što smo već vidjeli, paralaksa nije toliko udaljena pojava od nas, ona nas svugdje okružuje i uz pomoć nje vidimo onakvu kakva jest. Ovo je svakako zanimljivo i uzbudljivo, i zato biste trebali obratiti pozornost na metodu paralakse, makar i iz radoznalosti. Znanje nikada nije suvišno.

zaključak

Dakle, analizirali smo kakva je suština paralakse, zašto odrediti udaljenost od zvijezda nije potrebno imati složenu opremu, već samo teleskop i znanje o geometriji, kako se koristi u našem tijelu i zašto možemo biti toliko važni u svakodnevnom životu. Nadamo se da su vam informacije bile korisne!