Fizika: tlak krutih tvari, tekućina i plinova

Jedan od važnih parametara koji karakterizira tri osnovna stanja materije na različite načine (plin, krutinu i tekućinu) je tlak. U članku se razmatraju glavna pitanja fizike tlaka krutih tvari, tekućina i plinova.

Tri agregatna stanja materije

Prije nego se okrenemo pitanju pritiska u fizici, definiramo čvrsta, tekuća i plinovita tijela, koji su glavni načini postojanja materije na našem planetu.

Čvrsto tijelo praktično ne pokazuje fluidnost, a ta činjenica karakterizira glavnu razliku između krutina i tekućina i plinova. Čestice koje tvore krutinu (molekule, atomi) nalaze se u određenim prostornim položajima i vrlo rijetko ih mijenjaju. Zato svaki utjecaj vanjske sile na čvrsto tijelo dovodi do pojave suprotstavljenih sila u njemu, nastojeći sačuvati oblik i volumen.

Tekućine i plinovi su tekuća stanja materije, to jest, čak i minimalni utjecaj vanjske sile na njih će dovesti do promjene njihovog oblika. I u tekućinama i plinovima, čestice od kojih su sastavljene nemaju određeno mjesto u prostoru i konstantno skaču s jednog mjesta na drugo. Ta stanja tekućina razlikuju se u jačini interakcije između njihovih čestica. Tako, u tekućinama, sila interakcije između atoma i molekula, iako je red veličine manja od one u krutini, i dalje ostaje značajna kako bi se zadržao volumen koji zauzima tekućina. To znači da su tekućine praktički nekompresibilne. U plinovima se međutim može zanemariti sila interakcije između čestica koje ih tvore, tako da plinovi uvijek zauzimaju proizvoljno velik volumen koji im je na raspolaganju.

Napominjemo da postoji četvrto stanje materije - plazma, koje je po svojim svojstvima slično plinu, ali se razlikuje od njega po tome što su njegove karakteristike u velikoj mjeri određene magnetskim i električnim efektima. Većina materije u svemiru je upravo u stanju plazme.

Pojam tlaka u fizici

Da biste razumjeli što je pritisak, prvo morate razmotriti koncept sile. Sila u fizici razumijeva se kao intenzitet utjecaja ili interakcije između tijela. Primjerice, pri formuliranju drugog Newtonovog zakona, sila se shvaća kao fizička veličina bilo koje prirode, koja je sposobna dati određeno ubrzanje tijelu konačne mase. U Međunarodnom sustavu jedinica mjerena je sila u newtonima (N). Sila od 1 N može mijenjati brzinu tijela koje teži 1 kg po 1 m svake sekunde.

Tlak je količina koja se definira kao okomita komponenta sile koja se odnosi na površinu s određenim područjem, to jest:

P = F / S, gdje

P - tlak, S - područje, F - sila.

Mjerenje tlaka u fizici provodi se u paskalima (Pa), 1 [Pa] = 1 [H] / 1 [m2].

Ako sila F djeluje pod određenim kutom prema površini, tada je za izračunavanje tlaka potrebno odrediti okomitu komponentu sile na tu površinu. Sila koja djeluje tangencijalno na površinu ne stvara nikakav pritisak.

Krute tvari i tlak

Budući da je sila i površina udarca potrebna za stvaranje tlaka, to nije moguće u slučaju krutih tvari, jer su one u stanju ravnoteže. Doista, svaka čestica u krutini zauzima određeni položaj, a rezultirajuća sila koja djeluje na tu česticu iz svoje okoline je nula. Stoga, kada govorimo o fizici pritiska krutih tijela, mislimo na sudjelovanje vanjskih objekata s kojima ta tijela djeluju.

Na primjer, ako uzmete metalnu šipku i stavite je na pijesak s većom ravninom, tada će početi stvarati neki pritisak na površinu pijeska. Sada, ako stavimo istu građu na pijesak s manjim zrakoplovom, onda možemo vidjeti da će uroniti u pijesak na određenu dubinu. Uzrok ovog fenomena bit će različit tlak metalne šipke na pijesku u različitim položajima. Iz formule za tlak P = F / S, može se vidjeti da što je područje manje, to veći pritisak stvara čvrsto tijelo na površini nosača. U slučaju šipke, sila F ostala je konstantna u svim svojim položajima i bila je jednaka težini šipke:

m × g gdje

m i g su masa snopa i ubrzanje gravitacije.

Tlak tekućine

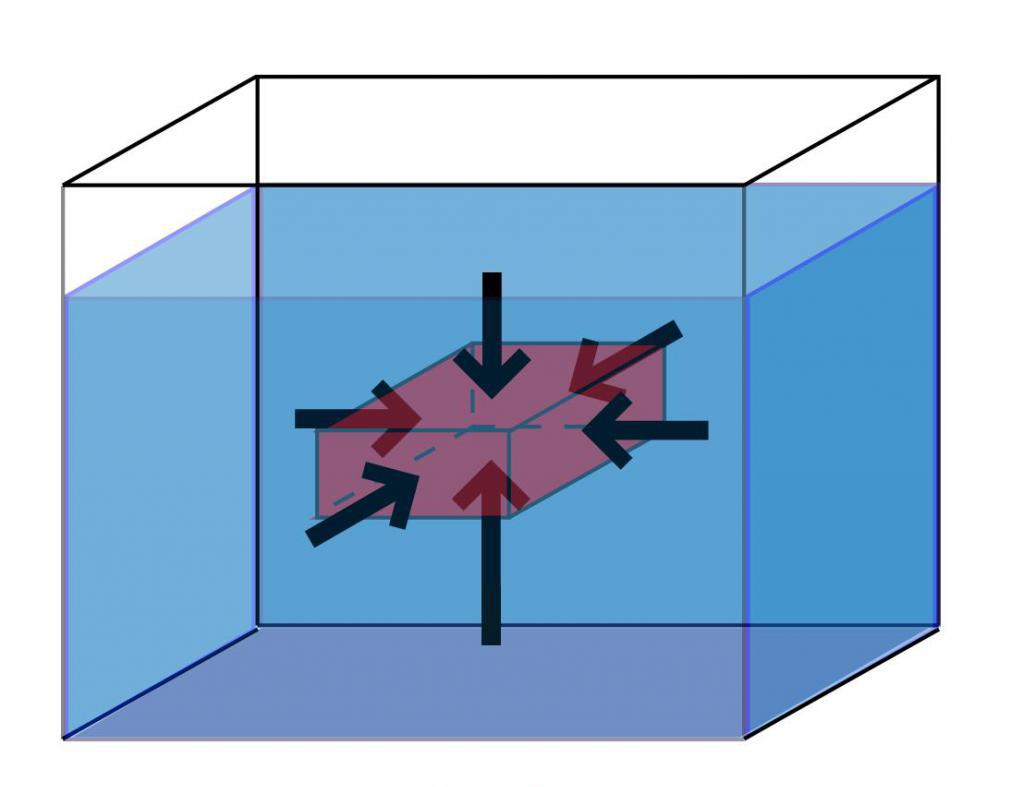
Budući da su plinovi i tekućine predstavnici tekućine, fiziku tlaka u tekućini i plinu karakterizira činjenica da oba stanja materije u bilo kojem beskonačno malom volumenu od njih vrše isti pritisak u svim prostornim smjerovima. Međutim, ako će volumen koji se razmatra imati neke konačne dimenzije, onda će za tekućine sila gravitacije početi igrati ulogu, s kojom gornji slojevi djeluju na donje slojeve. Ta sila dovodi do pojma hidrostatskog tlaka.

U fizici, hidrostatski tlak se definira kao tlak s kojim tekućina djeluje na tijelo uronjeno u njega. Taj se tlak izračunava pomoću formule:

P = ρ × g × h, gdje

ρ i h su gustoća i dubina tekućine.

Tlak u plinovitim medijima

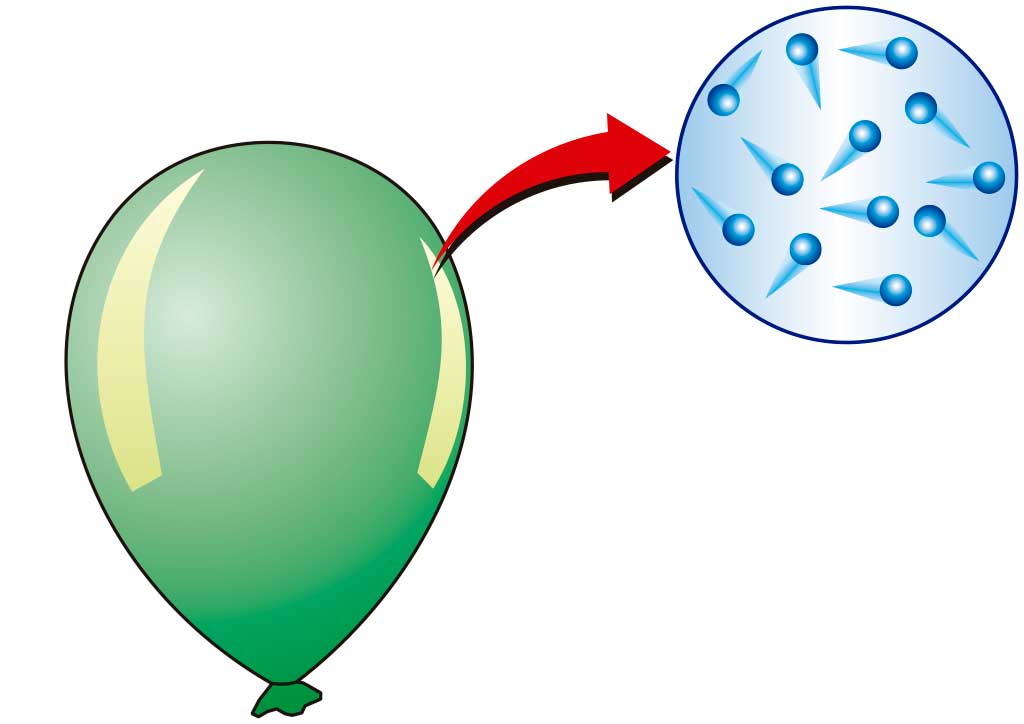
S obzirom na plinove, treba reći da je tlak u njima povezan isključivo s nasumičnim kretanjem atoma i molekula.

Pretpostavimo da postoji zatvoreni plin u nekoj posudi. Budući da se njegove čestice slučajno kreću u svim smjerovima na isti način, kada dođu do zidova posude, počinju ih udarati, tj. Stvarati pritisak. Naravno, utjecaj pojedinačne čestice stvorit će vrlo mali tlak, međutim, ako uzmemo u obzir da postoji mnogo tih čestica (redoslijedom Avogadrovog broja N _A = 6.02 * 10 ²³ ), te da se kreću velikom brzinom (oko 1000 m / s), tada tlak koji djeluje na zidove posude postaje vidljiv u praksi.

Za razliku od tekućina, čestice plinova međusobno ne djeluju (aproksimacija idealnog plina), stoga nema smisla govoriti o tlaku gornjih slojeva plina na niže.

Što određuje tlak u plinu?

Znajući prirodu pojave tlaka u plinovima, može se pretpostaviti da ako povećamo broj čestica koje udaraju u stijenke krvnih žila i povećamo snagu tih utjecaja, tada se tlak treba povećati. S tim u vezi, sljedeći čimbenici određuju promjenu tlaka u plinu.

• Koncentracija čestica Može se povećati smanjenjem volumena plina. Pri konstantnoj temperaturi, promjena volumena će obrnuto utjecati na tlak.
• Temperatura. Budući da ova vrijednost određuje kinetičku energiju čestica plina, njeno povećanje, uz ostale konstantne parametre sustava, dovodi do povećanja tlaka.

Pritisak zemljine atmosfere

Budući da je atmosfera našeg planeta mješavina plinova (uglavnom dušika i kisika), fizika atmosferskog tlaka neće se razlikovati od fizike opisa te količine za plinove. Dakle, tlak zraka na Zemljinoj površini je 101 325 Pa ili 100 kPa, što odgovara tlaku od 760 mm Hg.

S povećanjem nadmorske visine koncentracija molekula zraka počinje opadati, budući da se gravitacija smanjuje, a već na visini Mount Everesta (8.848 m), tlak zraka pada na 34 kPa, što je 1/3 tog tlaka na razini mora. Takvo smanjenje atmosferskog tlaka ozbiljna je prijetnja ljudskom životu.

Primjer rješavanja problema

Svako rješenje problema fizike na pritisak provodi se pomoću formula i koncepata o kojima se raspravlja u članku. Dajemo primjer rješavanja jednog od tih problema.

Iz praktičnih razloga, atmosferski tlak u fizici se obično izražava u milimetrima žive. Koji je tlak u milimetrima žive na vrhu Everesta?

Iz gore navedenih podataka je poznato da je na vrhu najviše planine na svijetu tlak zraka 34 kPa. Da bismo odredili visinu stupca žive, kako bi se uravnotežio taj atmosferski tlak, upotrijebimo formulu za hidrostatski tlak:

P = ρ × g × h,

odakle

h = P / (ρ × g), gdje

ρ = 13 540 kg / m ³ - gustoća žive,

g = 9,81 m / s ² .

Zamjenjujući poznate vrijednosti u formulu, dobivamo:

h = 0,256 m = 256 mm.

Taj se problem može riješiti na drugi način. Znajući da je tlak zraka blizu površine planeta 101 kPa, a to odgovara tlaku od 760 mm stupca žive, moguće je dobiti visinu stupca žive na visini Everesta jednostavnim omjerom:

h = 34 × 760/101 = 256 mm.