Znakovi sličnosti trokuta i njihova praktična primjena za rješavanje problema

Pojam sličnosti proizvoljan geometrijski oblici u biti, vrlo je lako objasniti, a još manje dokazati. Tako, primjerice, promatrajući objekt kroz povećalo, vidimo sliku ovog objekta koji je nekoliko puta povećan, sa očuvanim proporcijama svih njegovih dimenzija. Drugim riječima, slika objekta slična je izvornom objektu prije povećanja. U većini problema geometrije, dokazati proporcionalnost strana i područja trokuta primijeniti 3 glavna znaka. Da bi se razmotrili postojeći znakovi sličnosti trokuta, potrebno je u početku definirati ključni koncept koji će se u budućnosti koristiti u tekstu.

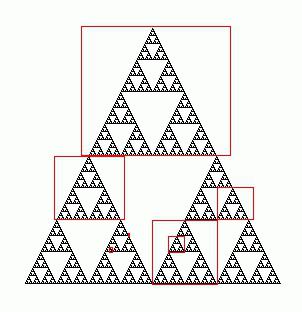
Dakle, trokuti su slični, ako su njihove slično smještene strane proporcionalne, a odgovarajuće raspoređeni kutovi su jednaki (valja se sjetiti da se strane nazivaju sličnim, ili odgovarajućim, ako su smještene nasuprot jednakim kutovima). Razmotrimo slične trokute CABC i 1A1B1C1. Prema navedenom konceptu, relevantne strane su: AB i A ₁ B ₁ , kao i parovi strana BC i B ₁ C ₁ , AC i A ₁ C ₁ . Imajte na umu da su stranice svakog od ova tri para nasuprotnih kutova iste veličine.

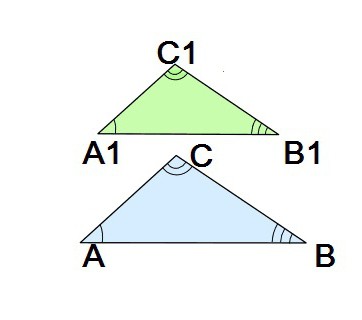Sličnost je označena poseban znak koja se nalazi između oznaka u pitanju: CABC _{1 1} A ₁ B ₁ C ₁ .

Omjer relevantnih strana s prisutnošću ove značajke je parametar koji se naziva koeficijent sličnosti k. Ako je k = 2, možemo reći da je jedna od dvije razmatrane geometrijske figure uvećana dvostruka kopija druge. Jasno je da ako je k = 1, onda su trokuti jednaki. Stoga se ta jednakost može smatrati posebnim slučajem njihove sličnosti.

Znakovi sličnosti trokuta

Ispostavlja se da za utvrđivanje prisutnosti razmatranog obilježja nema potrebe provjeravati sve zahtjeve navedene u tekstu gore navedene definicije sličnosti. Dovoljno je ispuniti minimalni skup uvjeta i to ćemo sada potvrditi u praksi.

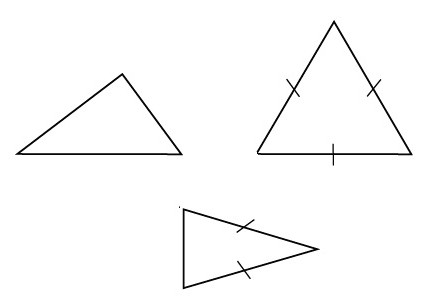
Prvi znak

Prilikom rješavanja problema, prvi znak sličnosti trokuta pojavljuje se u dokazima mnogo češće nego drugi. Imajte na umu da radi samo s dva elementa geometrijske figure: dva kuta. Preostali znakovi sličnosti trokuta zahtijevaju sudjelovanje tri elementa. Dakle, za dva proizvoljna slična trokuta, dva kuta jednog od njih jednaka su istim 2 kutovima drugog.

Dokaz

Prema osnovnim svojstvima koja vrijede za bilo koji proizvoljni trokut, za .C možemo napisati sljedeći izraz. Njegova vrijednost će biti jednaka (180 ° - (+A + )V)), za drugu ∠S ₁ vrijednost će se izračunati po istom principu. Elementarnim transformacijama izraza dobijamo da je =C = C ₁ . Tako su svi kutovi prisutni u ВAVS jednaki svim analognim kutovima koji se nalaze u ∆A ₁ V ₁ S ₁ . Sličnim algoritmom dokazani su i preostali znakovi sličnosti trokuta.

Drugi znak

Ovaj pristup dokazu se često koristi ako su poznati kutovi razmatranih geometrijskih figura.

Za dva slična trokuta, istina je da su dvije strane svake od njih proporcionalne drugoj sličnoj strani druge, a kutovi između tih parova strana jednaki su.

Dokaz

Da biste dokazali ovu značajku, morate pogledati prethodne izračune. Na temelju gore navedenih rezultata dovoljno je dokazati da je =V = V ₁ . Razmotrimo ∆ABC ₂ , za koje su, prema prvom znaku, istinite sljedeće tvrdnje: = ₁ = 1A ₁ , = ₂ = V ₁ . CABC ₂ ~ 1A ₁ V ₁ S ₁ . To znači AB / A ₁ B ₁ = AC ₂ / A ₁ C. S druge strane, poznato je iz uvjeta da vrijedi sljedeći odnos: AC / A ₁ C _{1 =} AB / A ₁ B ₁ . Kao rezultat toga dobivamo jednakost strana AC = AC ₂ , kao i tvrdnju da je CABC ~ CABC ₂ prema drugom znaku (AC = AC ₂ i =A = ∠1, jer je kao rezultat razmatranja početnih podataka utvrđeno da je A = 1A ₁ i = ₁ = 1A1, AB- je zajednička strana za ta dva trokuta). Iz dokaza slijedi da =B = ,2, a budući da je = ₂ = 1V ₁ , dobivamo da je =V = V ₁ . Iz toga slijedi da je dokazan još jedan znak.

Treći znak

Ta se značajka smatra najočiglednijom kada se dokazuje sličnost, jer se razmatraju sve strane tih trokuta s poznatim parametrima.

Dakle, za dva trokuta koja su slična jedan drugome, postoji tvrdnja da su 3 strane jedne od njih proporcionalne 3 odgovarajuće strane druge.

Dokaz

S obzirom na prethodnu značajku sličnosti, sada je za konstruiranje dokaza dovoljno samo utvrditi da postoji jednakost oblika: =A = 1A ₁ . U tu svrhu uzmite u obzir bilo koje proizvoljno CABC ₂ , za koje je = ₁ = 1A ₁ , 2 = V ₁ . Prema 1. atributu CABC ₂ ∆ ∆A ₁ B ₁ C ₁ , za ta dva trokuta možemo napisati omjer tipa AB / A ₁ B ₁ = BC ₂ / B ₁ C ₁ = C ₂ A / C ₁ A _1, iz koje možemo napisati jednakost oblika: B ₁ C ₁ = BC ₂ , A ₁ C ₁ = AC ₂ . Iz ovoga je logično zaključiti da CABC ∆ ∆ABC _2, i, kao zaključak, AndA i 1A1 su jednaki. Iz toga slijedi da je dokazana i razmatrana značajka.

nekretnine

1. Za dva trokuta, slična jedan drugome, omjer vrijednosti njihovih područja je izravno proporcionalan kvadratu koeficijenta. Dokaz. Razmotrimo dvije proizvoljne figure s tri strane i tri kuta koji su međusobno slični. Neka su A i A ₁ odgovarajuće strane tih figura, a h i h ₁ su odgovarajuće visine. Neka je k koeficijent sličnosti za razmatrane trokute, dakle iz omjera slike možemo napisati jednadžbu oblika: A ₁ = k * A. Lako je vidjeti da za omjer visine možemo napisati jednadžbu oblika: h ₁ = k * h. Za omjer područja razmatranih geometrijskih figura dobivamo: S ₁ / S = (1 / 2a ₁ h ₁ ) / (1 / 2ah) = (a ₁ / a) * (h ₁ / h) = k * k = k ² . Dakle, kada se trokut „rastegne“ 2 puta, njegova se površina povećava za 2 ² = 4 puta. Drugo svojstvo slijedi iz prethodnog dokaza i izravno je s njim povezano.
2. Svi odgovarajući pravci nacrtani u takvim trokutima također su proporcionalni jedan drugome i jednaki su gore navedenoj vrijednosti koeficijenta. To jest, prema navedenom svojstvu, može se tvrditi da će sve unutarnje dodatne konstrukcije također biti proporcionalne.

Dodavanje glavnog popisa znakova

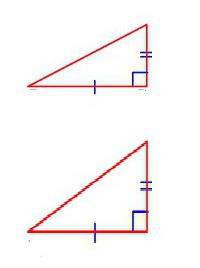
Vrijedi razmotriti niz pojedinačnih značajki koje su primjenjive na geometrijske oblike određenog tipa. Tako su pravi trokuti slični ako:

• njihova hipotenuza i bilo koja od dvije noge su proporcionalne;
• ako su njihovi odgovarajući oštri kutovi jednaki;
• ako su sve noge razmatranih trokuta parno proporcionalne.

zaključak

Tako smo spojili sve moguće znakove, uz pomoć kojih se nekako može dokazati sličnost dviju ili više figura s tri ugla i strane, bez obzira na njihov tip i svojstva. U većini problema u geometriji, glavna tri znaka koriste se za dokazivanje proporcionalnosti strana i područja, ali nismo zanemarili niz znakova sličnosti koji su primjenjivi samo ako je potrebno izvesti dokaz za dotične geometrijske figure pod pravim kutom. Ovi znakovi sličnosti desni trokuti uvelike pojednostavljuju proces rješavanja raznih vrsta zadataka i zahtijevaju minimum podataka za njih.