Jednostavan zadatak: kako pronaći perimetar?

Znanje kako pronaći perimetar, učenici dobivaju više u osnovnoj školi. Tada se ta informacija stalno koristi tijekom tečaja matematike i geometrije.

Opća teorija za sve brojke

Stranke su obično označene latiničnim slovima. Štoviše, mogu se označiti kao segmenti. Zatim su za svaku stranu potrebna dva slova i napisana su velika. Ili unesite oznaku jednog slova, koje će sigurno biti malo.
Slova se uvijek biraju po abecedi. Za trokut će biti prva tri. Šesterokut će imati 6 - od a do f. To je prikladno za uvođenje formula.

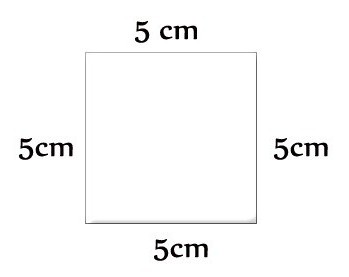
Sada kako pronaći perimetar. To je zbroj duljina svih strana na slici. Broj stavki ovisi o njegovoj vrsti. Perimetar je označen latiničnim slovom R. Mjerne jedinice podudaraju se s onima koje su dane strankama.

Formule perimetara različitih oblika

Za trokut: P = a + b + c. Ako je jednakokračan, tada se formula pretvara: P = 2a + c. Kako pronaći perimetar trokuta, ako je jednakostraničan? To će pomoći: P = 3a.

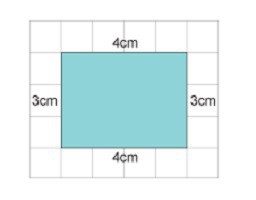
Za proizvoljni četverokut: P = a + b + c + d. Njegov poseban slučaj je kvadrat, perimetarska formula: P = 4a. Postoji pravokutnik, onda je potrebna sljedeća jednakost: P = 2 (a + b).

Što ako je nepoznata dužina jedne ili više strana trokuta?

Iskoristite prednost kosinusni teorem ako postoje dvije strane podataka i kut između njih, koji je označen slovom A. Tada, prije pronalaženja perimetra, morat ćete izračunati treću stranu. Za to je korisna sljedeća formula: s² = a² + v² - 2 av cos (A).

Poseban slučaj ovog teorema formulira Pitagora za pravokutni trokut. U njoj, kosinusna vrijednost pravog kuta postaje nula, što znači da posljednji izraz jednostavno nestaje.

Postoje situacije kada naučiti kako pronaći na obodu trokuta može biti na jednoj strani. Ali u isto vrijeme poznati su i kutovi figure. Ovdje se spasava sinusni teorem kada je omjer duljina stranica prema sinusima odgovarajućih suprotnih kutova jednak.

U situaciji kada područje mora biti prepoznato od strane područja, druge formule će biti korisne. Primjerice, ako je poznat radijus upisane kružnice, onda je pitanje kako pronaći perimetar trokuta, sljedeća formula korisna: S = p * r, ovdje p je polu-perimetar. Ona mora biti izvedena iz ove formule i pomnožena s dva.

Primjeri zadataka

Stanje prvog. Otkrijte obod trokuta čije su stranice 3, 4 i 5 cm.
Odluka. Potrebno je upotrijebiti jednadžbu, koja je gore navedena, i samo zamijeniti podatke u problemu vrijednosti u nju. Proračuni su jednostavni, dovode do broja od 12 cm.
Odgovor je. Obod trokuta je 12 cm.

Drugi uvjet. Jedna strana trokuta je 10 cm, a poznato je da je druga 2 cm veća od prve, a treća 1,5 puta veća od prve. Potrebno je izračunati njegov perimetar.
Odluka . Da biste to saznali, morate računati dvije strane. Drugi se određuje kao zbroj 10 i 2, a treći je proizvod 10 i 1,5. Tada ostaje samo brojati zbroj triju vrijednosti: 10, 12 i 15. Rezultat će biti 37 cm.
Odgovor je. Opseg je 37 cm.

Stanje trećeg. Ima pravokutnik i kvadrat. Jedna strana pravokutnika je 4 cm, a druga 3 cm duža. Potrebno je izračunati vrijednost strane kvadrata, ako je njezin perimetar 6 cm manji od pravokutnika.
Odluka. Druga strana pravokutnika je 7. Znajući to, lako je izračunati njezin perimetar. Izračun daje 22 cm.
Da biste pronašli stranu kvadrata, najprije morate oduzeti 6 s perimetra pravokutnika, a zatim ga podijeliti na 4. Kao rezultat, imamo broj 4.
Odgovor je. Bočni trg 4 cm.