Tijelo je bačeno pod kutom prema horizontu: brzina, domet i nadmorska visina

U ovom članku ćemo analizirati situaciju kada je tijelo bačeno pod kutom prema horizontu. To bi moglo biti bacanje kamena s rukom, pucanj iz topa, lansiranje strijele s lukom, i tako dalje. Sve navedene situacije opisane su jednako s matematičkog stajališta.

Značajka kretanja pod kutom prema horizontu

Koje su sličnosti gore navedenih primjera s gledišta fizike? Ona leži u prirodi sila koje djeluju na tijelo. Tijekom slobodnog leta određenog tijela na njega djeluju samo dvije sile:

• Gravitacija.
• Otpor zraka

Ako je tjelesna težina dovoljno velika, a njezin oblik je istaknut (projektil, strelica), tada se može zanemariti otpor zraka.

Tako je kretanje predmeta koji je bačen pod kutom prema horizontu tijela zadatak u kojem se pojavljuje samo sila gravitacije. To je ono što određuje oblik putanje, koja je s dobrom točnošću opisana paraboličnom funkcijom.

Jednadžbe gibanja duž parabolične putanje. Brzina

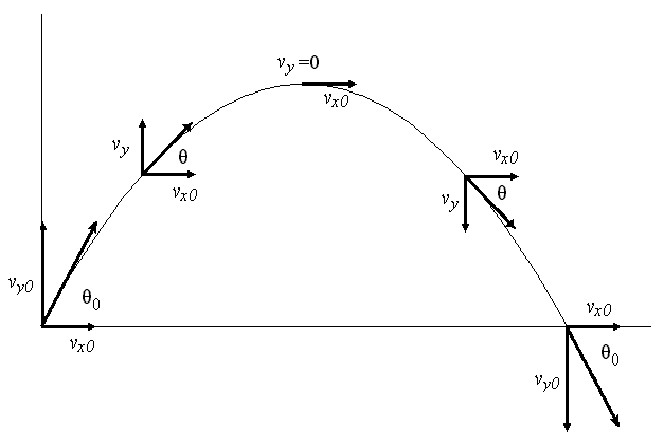
Tijelo je bačeno pod kutom prema horizontu. Kako možete opisati njegov pokret? Budući da je jedina sila koja djeluje tijekom leta tijela usmjerena prema dolje, njezina horizontalna komponenta je nula. Ta činjenica znači da je horizontalno kretanje objekta jedinstveno određeno početnim uvjetima (kut ubacivanja ili udarca θ i brzina v). Vertikalno kretanje tijela živ je primjer ravnomjerno ubrzanog gibanja, pri čemu konstanta g ima ulogu u ubrzanju (9,81 m / s ² ).

S obzirom na gore navedeno, možemo napisati dvije komponente za brzinu letećeg tijela u trenutku t:

vx = v * cos (θ);

v _y = v * sin (θ) - g * t

Kao što se može vidjeti, komponenta v _x ne ovisi o vremenu i ostaje konstantna tijekom cijele putanje leta (zbog odsutnosti vanjskih sila u smjeru osi x). Komponenta v _y ima maksimum u početnom trenutku vremena. A onda se počinje smanjivati ​​sve do točke da nestaje na maksimalnoj točki polijetanja tijela. Nakon toga mijenja svoj znak i u trenutku pada ispostavlja se da je jednak modulu početne komponente v _y , odnosno v * sin (θ).

Pisane jednadžbe omogućuju nam određivanje brzine tijela bačenog pod kutom prema horizontu u bilo kojem trenutku t. Modul će biti jednak:

v = √ (v _x ² + v _y ² ) = √ (v ² * cos ² (θ) + v ² * sin ² (θ) - 2 * v * sin (θ) * g * t + g ² * t ² ) =

= √ (v ² - 2 * v * sin (θ) * g * t + g ² * t ² )

Jednadžbe gibanja duž parabolične putanje. Raspon leta

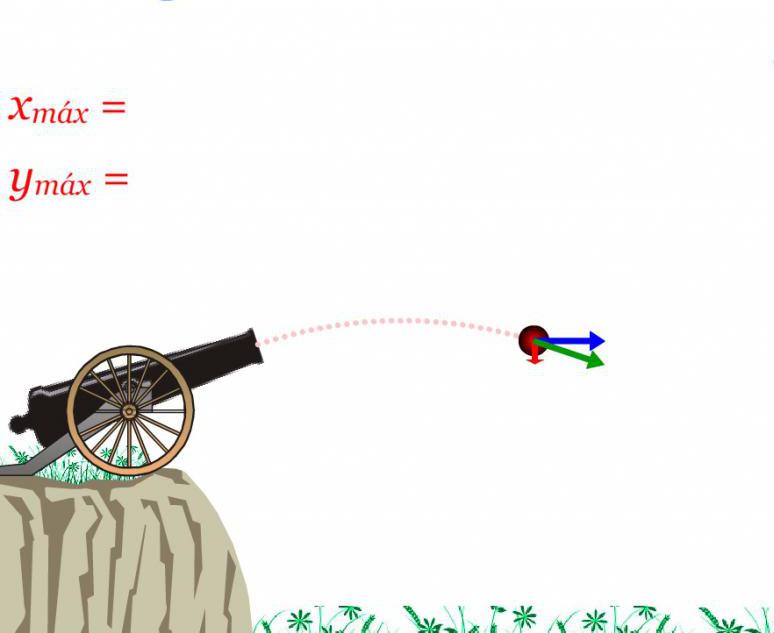
Tijelo je bačeno pod kutom prema horizontu. Kakva će to udaljenost letjeti? Pitanje raspona leta odnosi se na promjenu koordinate x. Tu je vrijednost moguće pronaći ako integriramo obje komponente brzine tijekom vremena. Kao rezultat integracije dobivamo formule:

x = v * cos (θ) * t + x ₀ ;

y = v * sin (θ) * t - g * t 2/2 + y ₀

Razlika u x i x ₀ koordinatama je raspon. Ako pretpostavimo da je x ₀ = 0, tada će raspon biti jednak x, kako biste pronašli ono što trebate znati koliko dugo će tijelo biti u zraku.

Druga jednadžba omogućuje izračun tog vremena, pod uvjetom da _je poznata vrijednost y ₀ (visina h, iz koje je tijelo bačeno). Kada objekt dovrši svoje kretanje (padne na tlo), njegova y koordinata će se pretvoriti u nulu. Izračunajte vrijeme kada se to dogodi. Imamo:

v * sin (θ) * t - g * t 2/2 + h = 0

Pred nama je potpuna ravnopravnost. Rješavamo ga putem diskriminanta:

D = v ² * sin ² (θ) - 4 * (-g / 2) * h = v ² * sin ² (θ) + 2 * g * h;

t = (-v * sin (θ) ± √D) / (2 * (-g / 2))

Odbijamo negativni korijen. Dobivamo sljedeće vrijeme leta:

t = (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)) / g

Sada ćemo tu vrijednost zamijeniti jednakošću za raspon leta. Dobivamo:

x = v * cos (θ) * (v * sin (θ) + √ (v ² * sin ² (θ) + 2 * g * h)) / g

Ako je tijelo bačeno s tla, to jest, h = 0, tada će ova formula biti mnogo jednostavnija. I uzmite oblik:

x = 2 * v ² * cos (θ) * sin (θ) / g = v ² * sin (2 * θ) / g

Posljednji izraz dobiven je uporabom veze između trigonometrijskih funkcija sinusa i kosinusa (formula redukcije).

Budući da sinus ima maksimalnu vrijednost za pravi kut, tada se maksimalni raspon postiže kada se tijelo baca (ispucava) iz tla pod kutom od 45 °, a taj raspon je jednak:

x = v2 / g

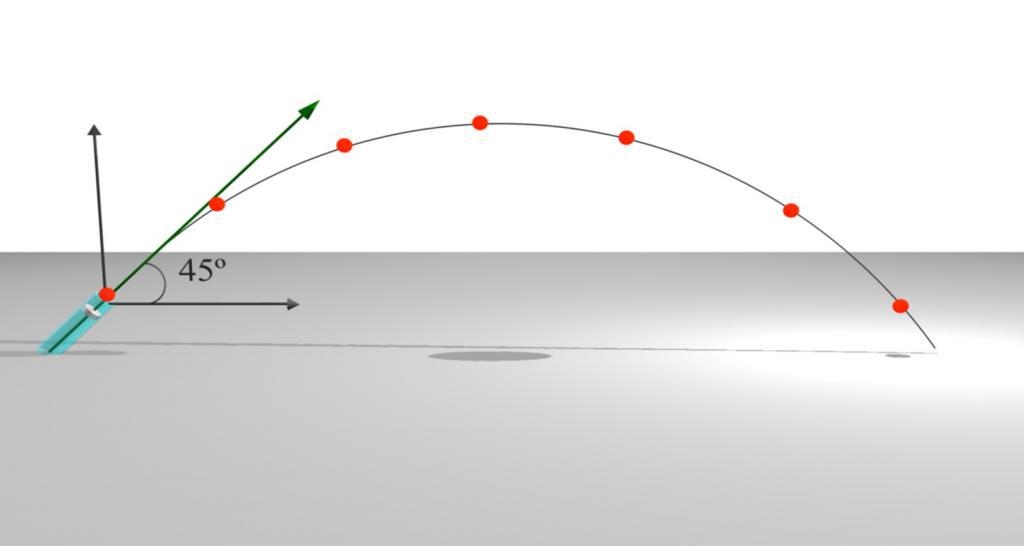
Visina tijela, bačena pod kutom prema horizontu

Sada definiramo još jedan važan parametar - visinu do koje napušteni objekt može penjati. Očito, za to je dovoljno uzeti u obzir samo promjenu y koordinate.

Dakle, tijelo je bačeno pod kutom prema horizontu, do koje visine bi ga uzletjelo? Ta visina će odgovarati jednakosti nuli komponente brzine _{y y} . Imamo jednadžbu:

v _y = v * sin (θ) - g * t = 0

Riješite jednadžbu. Dobivamo:

t = v * sin (θ) / g

Sada biste to vrijeme trebali zamijeniti izrazom za y koordinatu. Dobivamo:

y = v * sin (θ) * t - g * t 2/2 + h = v ² * sin ² (θ) / g - g / 2 * v ² * sin ² (θ) / g ² + h =

= v ² * sin ² (θ) / (2 * g) + h

Ova formula sugerira da je maksimalna visina, za razliku od raspona leta, dobivena bacanjem tijela vertikalno (θ = 90). U ovom slučaju dolazimo do formule:

y = v2 / (2 * g) + h

Zanimljivo je napomenuti da se u svim formulama navedenim u ovom članku ne pojavljuje tjelesna masa. Značajke parabolične putanje su neovisne o njoj, ali samo u odsutnosti otpora zraka.