Povijest Pitagorina teorema. Dokaz teorema

Oni koji su zainteresirani za povijest Pitagorina teorema, koji se proučava u školskom kurikulumu, također će znatiželjno znati da će 1940. godine biti objavljena knjiga s tristo sedamdeset dokaza te naizgled jednostavne teoreme. No intrigirala je umove mnogih matematičara i filozofa različitih razdoblja. U Guinnessovoj knjizi rekorda ona je fiksirana kao teorem s maksimalnim brojem dokaza.

Povijest Pitagorina teorema

Povezan s imenom Pitagore, teorem je bio poznat mnogo prije rođenja velikog filozofa. Tako je u Egiptu, tijekom izgradnje građevina, uzet u obzir omjer pravog trokuta prije pet tisuća godina. Babilonski tekstovi odnose se na isti omjer slike. pravokutni trokut 1200 godina prije rođenja Pitagore.

Postavlja se pitanje zašto onda priča kaže - pojava Pitagorina teorema pripada njemu? Odgovor može biti samo jedan - dokazao je omjer širine i visine u trokutu. Učinio je ono što su prije nekoliko stoljeća oni koji su jednostavno koristili odnos omjera i hipotenuza empirijski uspostavljeni.

Iz života Pitagore

Velika budućnost znanstvenik, matematičar, Filozof je rođen na otoku Samosu 570. pr. Kr. Povijesni dokumenti sačuvali su podatke o ocu Pitagore, koji je bio rezbar za dragocjeno kamenje, ali nema informacija o majci. Rečeno je o dječaku koji je rođen da je izvanredno dijete koje je od djetinjstva pokazivalo strast prema glazbi i poeziji. Povjesničari pripisuju učitelje mladih Pitagore Herdomadantu i Ferekidu Syrosu. Prvi je uveo dječaka u svijet muza, a drugi, kao filozof i utemeljitelj talijanske filozofske škole, usmjerio je mladićev pogled prema logosu.

Sa 22 godine (548. pr. Kr.) Pitagora je otišao u Nookratis kako bi proučavao jezik i religiju Egipćana. Nadalje, njegov put je ležao u Memphisu, gdje je, zahvaljujući svećenicima, nakon što je prošao genijalne testove, shvatio egipatsku geometriju, što je možda potaknulo znatiželjnog mladića da dokaže Pitagorin teorem. Povijest će ovaj teorem pripisati teoremu u budućnosti.

Zarobio ga je kralj Babilon

Na putu kući u Hellas, Pitagora je zarobljen od strane kralja Babilona. No, biti u zatočeništvu koristio je znatiželjni um matematičara početnika, on je morao nešto naučiti. Doista, u tim godinama, matematika u Babilonu bila je razvijenija nego u Egiptu. Proveo je dvanaest godina proučavajući matematiku, geometriju i magiju. Vjerojatno je upravo babilonska geometrija bila uključena u dokazivanje omjera aspekta trokuta i povijesti otkrića teorema. Pitagora je imao dovoljno znanja i vremena za to. Ali da se to dogodilo u Babilonu, nema dokumentarne potvrde ili pobijanja.

530. godine prije Krista Pitagora bježi iz zatočeništva u svoju domovinu, gdje živi na dvoru tiranina Polycrata u statusu polu-ploče. Takav život ne odgovara Pitagori, a on se povlači u špilje na Samosu, a zatim odlazi na jug Italije, gdje se tada nalazila grčka kolonija Croton.

Tajni redovni red

Na temelju te kolonije Pitagora je organizirao tajni redovni red koji je ujedno bio i vjerska zajednica i znanstveno društvo. Ovo društvo je imalo svoju vlastitu povelju, koja se odnosila na poštivanje određenog načina života.

Pitagora je tvrdio da, da bi razumio Boga, osoba mora naučiti takve znanosti kao algebra i geometrija, znati astronomiju i razumjeti glazbu. Istraživački rad sveden je na poznavanje mistične strane brojeva i filozofije. Treba napomenuti da principi koje je u to vrijeme propovijedao Pitagora imaju smisla čak iu sadašnjosti.

Mnoga otkrića koja su načinili učenici Pitagore pripisivana su njemu. Ipak, ako kratko govorimo, povijest stvaranja Pitagorina teorema drevnih povjesničara i biografa tog vremena izravno je povezana s imenom tog filozofa, mislioca i matematičara.

Učenja Pitagore

Možda je pomisao na povezanost teorema s imenom Pitagore navela povjesničare da kažu veliki Grk da su svi fenomeni našeg života kodirani u zloglasnom trokutu njegovim nogama i hipotenuza. I ovaj trokut je "ključ" za rješavanje svih problema koji se pojavljuju. Veliki filozof je rekao da treba vidjeti trokut, onda možemo pretpostaviti da je problem riješen za dvije trećine.

Pitagora je govorio o svom podučavanju samo usmeno svojim učenicima, ne praveći nikakve bilješke, čuvajući tajnu. Nažalost, učenje najvećeg filozofa do danas nije preživjelo. Nešto od njega je iscurilo, ali se ne može reći koliko je istinito i koliko je pogrešno u onome što je postalo poznato. Čak is poviješću Pitagorina teorema, nije sve nesporno. Povjesničari matematike sumnjaju u autorstvo Pitagore, prema njihovom mišljenju, teorem je korišten mnogo stoljeća prije njegova rođenja.

Pitagorin teorem

Može se činiti čudnim, ali ne postoji povijesni dokaz o teoremu samoga Pitagore - ne u arhivima, niti u bilo kojim drugim izvorima. U suvremenoj verziji smatra se da ne pripada nikome drugome nego samom Euclidu.

Postoje dokazi da je jedan od najvećih povjesničara matematike, Moritz Cantor, otkrio na papirusu pohranjenom u Berlinskom muzeju, koji su zabilježili Egipćani oko 2300. godine prije Krista. e. jednakost, koja glasi: 3² + 4² = 5².

Ukratko iz povijesti Pitagorina teorema

Formulacija teorema iz euklidskih "principa", u prijevodu, zvuči isto kao iu suvremenoj interpretaciji. U njemu nema novog očitavanja: kvadrat suprotne strane pravog kuta jednak je zbroju kvadrata stranica susjednih pravom kutu. Činjenica da su drevne indijske i kineske civilizacije koristile teorem potvrđena je u raspravi Zhou - bi suan jin. Sadrži informacije o egipatskom trokutu, koji opisuje omjer širine i visine 3: 4: 5.

Ne manje zanimljiva je i druga kineska matematička knjiga, Chu-Pei, koja također spominje pitagorejski trokut s objašnjenjem i crtežima koji se podudaraju s crtežima hinduističke geometrije Bashare. O samom trokutu u knjizi piše da ako se pravi kut može razložiti na njegove sastavne dijelove, onda će linija koja spaja krajeve strana biti jednaka pet, ako je baza tri, a visina četiri.

Indijska rasprava "Sulva sutra" iz VII-V stoljeća prije Krista. npr., govori o izgradnji pravog kuta pomoću egipatskog trokuta.

Dokaz teorema

U srednjem vijeku učenici su dokaz teorema smatrali preteškim. Slabi studenti pamte teoreme napamet, bez razumijevanja značenja dokaza. U tom smislu, dobili su nadimak "magarci", jer im je Pitagorin teorem bio nepremostiva prepreka, kao most za guzicu. U srednjem vijeku učenici su došli na šalu na temu ovog teorema.

Da bi se dokazao Pitagorin teorem na najlakši način, treba jednostavno izmjeriti njegove strane, bez upotrebe koncepta kvadrata u dokazu. Duljina strane nasuprot pravom kutu je c, a susjedni a i b, kao rezultat dobivamo jednadžbu: a ² + b ² = c ² . Ova tvrdnja, kao što je gore spomenuto, potvrđena je mjerenjem duljina stranica pravokutnog trokuta.

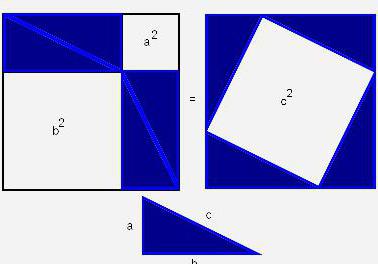
Ako započnemo dokaz teorema razmatrajući područje pravokutnika izgrađenih na stranama trokuta, možemo odrediti područje cijele figure. Ona će biti jednaka površini kvadrata sa stranom (a + b), as druge strane zbroj područja četiriju trokuta i unutarnjeg kvadrata.

(a + b) ² = 4 x ab / 2 + c2;

a2 + 2ab + b2;

c ² = a ² + b ² , prema potrebi.

Praktični značaj Pitagorina teorema je u tome što se može koristiti za pronalaženje duljina segmenata bez njihovog mjerenja. Prilikom izgradnje objekata izračunavaju se udaljenosti, položaj nosača i greda, određuju se težišta. Pitagorin teorem koristi se u svim modernim tehnologijama. Nismo zaboravili teorem pri stvaranju filmova u 3D-6D-dimenzijama, gdje se uz 3 uobičajene vrijednosti uzimaju u obzir visina, duljina, širina - vrijeme, miris i okus. Kako su ukusi i mirisi povezani s teoremom - pitate? Vrlo je jednostavno - kada pokažete film trebate izračunati gdje i što miriše i okusi poslati u gledalište.

Hoće li i dalje biti. Zahtjevni umovi čekaju neograničeni prostor za otkrivanje i stvaranje novih tehnologija.