Fenomen refrakcije. Kutovi loma i pada. Očita dubina spremnika
Fenomen refrakcije je vizualni efekt koji nastaje kada snop svjetlosti prelazi granicu između dva medija koji su joj prozirni. Važne karakteristike ovog učinka su indeksi loma i kutovi upadanja i refrakcije. U članku ćemo detaljnije razmotriti ovaj optički fenomen.
Snellov zakon za fenomen refrakcije
Kao što znate, svaki val, uključujući elektromagnetski, širi se ravnom linijom i konstantnom brzinom u homogenom materijalu. Čim se pojave kršenja homogenosti ovog materijala, val mijenja svoju pravocrtnu putanju. Živopisan primjer takve promjene je prelamanje svjetlosti.
Refrakcija grede javlja se na lokaliziranoj točki u prostoru, koja se nalazi na sučelju dva prozirna medija s različitim fizičkim karakteristikama. Na primjer, ova okruženja mogu biti staklo, zrak, voda, prozirna plastika i drugi. Kada udari u drugi medij, svjetlo odstupa za određeni kut od izvorne putanje.
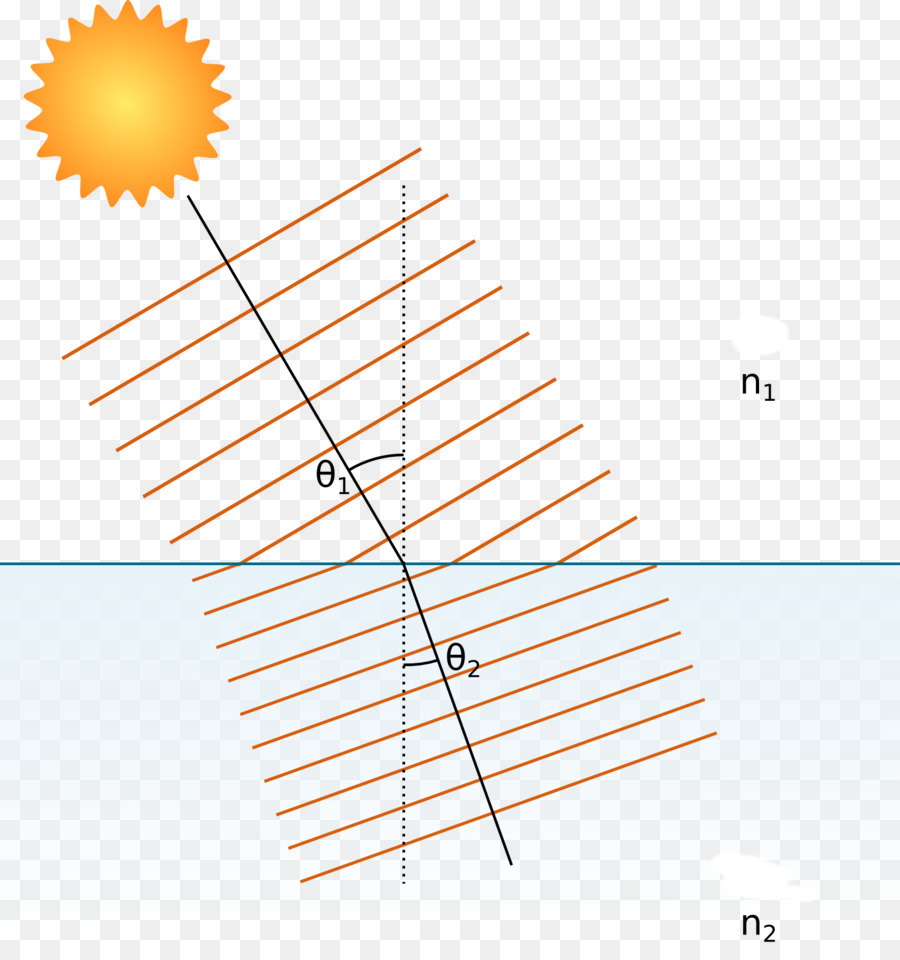
Ako mentalno povučete okomicu kroz točku gdje zrake presijeca ravninu razdvajanja medija i odredite kut između okomice i zrake kao θ 1 , te kut između iste okomice i zrake koja je prošla u drugi medij, kao θ 2 , tada slijedi sljedeći odnos:
sin (θ 1 ) * n 1 = sin (θ 2 ) * n 2
Kutovi theta jedan (θ 1 ) i theta dva (θ 2 ) nazivaju se kutovi upada, odnosno lom. Vrijednosti n 1 , n 2 važne su optičke karakteristike prvog i drugog medija, zovu se indeksi loma.
Gornja formula naziva se Snellov zakon (Snellius), budući da ju je nizozemski znanstvenik Willebrord Snellus početkom XVII. Stoljeća prvi put formulirao u svom modernom obliku, analizirajući veliku količinu eksperimentalnog materijala.

Indeks loma
Prema matematičkoj definiciji te fizičke veličine, ona je jednaka omjeru dviju brzina svjetlosti: u vakuumu iu materijalu, to jest:
n = c / v
Budući da je c> v, tada će n uvijek biti veći od jedan.
Indeks refrakcije ima različite vrijednosti za različite tvari. Na primjer, za zrak je gotovo jednak 1, a za vodu 1,33. Vrijednost n također ovisi o kemijskom sastavu istog materijala. Na primjer, indeks loma stakla ovisi o vrsti potonjeg i kreće se od 1,5 do 1,66.
Osim svojstava materijala, n varira jako, ako promijenite frekvenciju svjetla u snopu. Kut loma plavog svjetla je uvijek veći od crvenog. Brojke dane u prethodnom odlomku odnose se na žuti dio spektra koji je vidljiv čovjeku (λ ≈ 590 nm).
Optička gustoća medija
Ta fizička karakteristika određuje koliko snažno medij usporava brzinu svjetlosti. Optička gustoća je jedinstveno određena indeksom loma. Na primjer, voda je optički gusta od zraka, a svaka vrsta stakla je gusta od vode.
Ako pogledate Snell-ovu formulu, možete vidjeti da što je veća optička gustoća medija, to je niži kut normale svjetlo u njemu. Ovaj zaključak vrijedi bez obzira iz kojeg medija i u koju svjetlost će zraka pasti. Dakle, kada se razmatra granica voda-zrak, kut loma će biti manji od kuta upada ako se snop pomakne u vodu. Ako promijenite smjer snopa, kut upadanja će biti manji.
Izazov primjene Snellovog zakona
Poznato je da zraka svjetlosti pada na površinu vode pod kutom od 32 o . Potrebno je odrediti kut prelamanja svjetlosti, kao i veličinu njegove promjene, ako kut upadanja povećate za 10 o .
Količina refrakcije svjetlosti može se odrediti iz Snellovog zakona. Imamo:
θ 2 = arcsin (sin (θ 1 ) * n 1 / n 2 )
Budući da svjetlost pada iz zraka u vodu, tada je n 1 = 1 i n 2 = 1,33. Znajući da θ 1 = 32 o , dobivamo:
θ 2 = arcsin (sin (32 o ) * 1 / 1,33) = 23,48 o
Kao što možete vidjeti, kut se značajno smanjio. Sada izračunamo kut loma zraka, ako je θ 1 = 42 o . Koristeći istu formulu, dobivamo:
θ 2 = arcsin (sin (42 o ) * 1 / 1,33) = 30,21 o
Uzmite razliku između dobivenih kuteva:
30,21 o - 23,48 o = 6,73 o
Dobiveni rezultat znači da promjene između kutova upadanja i loma nisu linearne. Povećanje kuta upada za 10 o dovelo je do promjene u kutu loma samo za 6,7 o .
Zadatak određivanja prividne dubine

Mnogi su primijetili da ako pogledate dno rezervoara, onda kamenje leži na njemu i rastuće alge izgledaju blizu površine. Izračunajte, koristeći zakon loma, kako se stvarne i prividne dubine međusobno razlikuju. Za to ćemo uzeti u obzir male kutove incidencije, tj. Promatrač gleda okomito dolje na dno spremnika. Slijedi odgovarajući broj.
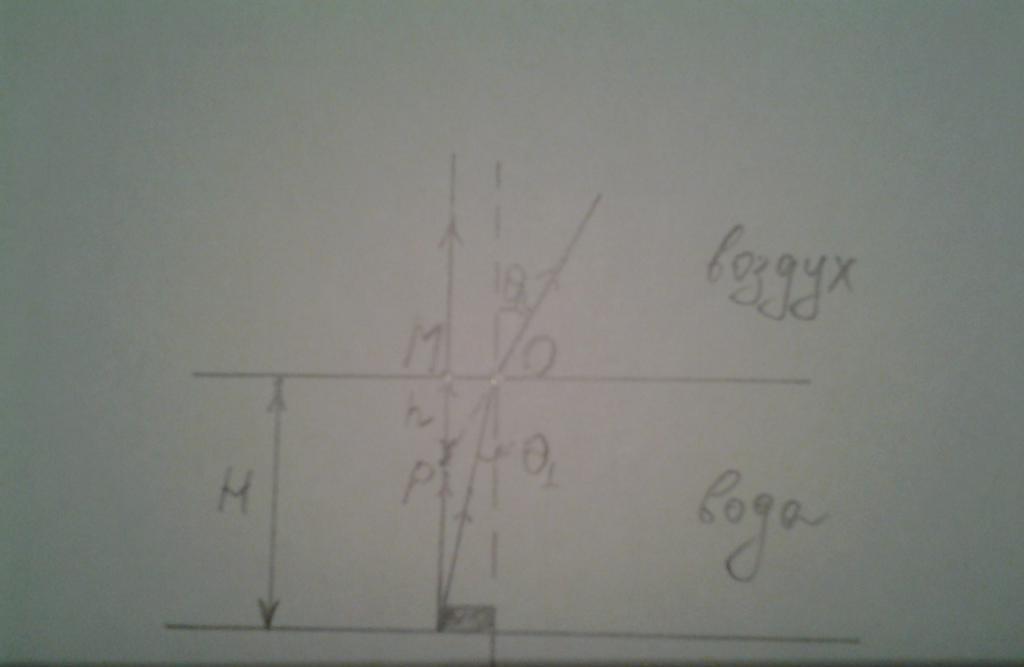
Slika prikazuje objekt koji leži na dnu. Budući da će se dvije grede koje izlaze iz iste točke objekta presjeći u točki P za promatrača, dubina h = MP bit će očita.
Da biste pronašli h, razmislite o pravom trokutu POM. MO interval je H * tg (θ 1 ), POM kut je 90 - θ2. Sada možete napisati:
tg (90-θ 2 ) = h / (H * tg (θ 1 ))
Znajući da je tangens jednak omjeru sinusa i kosinusa, te koristeći formule za trigonometrijske funkcije, možemo preformulirati ovu jednakost na sljedeći način:
cos (θ 2 ) / sin (θ 2 ) = cos (θ 1 ) * h / (H * sin (θ 1 ))
Budući da razmatramo male kutove (blizu vertikale), kosinusi će biti gotovo jednaki jedinicama, tako da će posljednja formula biti pojednostavljena u oblik:
h = h * sin (θ 1 ) / sin (θ 2 )
Ali omjer sinusa jednak je inverznom omjeru indeksa loma medija prema Snellovom zakonu, stoga zapisujemo:
h = H * n 2 / n 1
Kako se snop izlazi iz vode, n2 je indikator za zrak, koji je jednak jednom. Konačna formula za prividnu dubinu spremnika kada se gleda okomito je:
h = h / n, gdje je n = 1.33
Dakle, prividna dubina je približno 25% manja od stvarne.