Translacijsko gibanje: definicija, formule, teorem

Mehanika razmatra sve moguće pomake materijalne točke i čvrstog tijela. Svi su opisani u nekoliko dijelova. Na primjer, pitanje kako će se kretati bit će povlastica kinematike. U njemu se detaljno opisuje translacijsko kretanje, kao i složenije - rotacijsko. Prvo, to je lakše. Jer bez toga je teško preći na sljedeće teme.

Koje pretpostavke dopušta mehaničar?

U mnogim problemima dopušteno je uvesti aproksimaciju. To je zbog činjenice da neće utjecati na rezultat, ali će pojednostaviti tijek rasuđivanja.

Prva aproksimacija odnosi se na veličinu tijela. Ako je tijelo koje se razmatra znatno manje od ostalih u istom referentnom okviru, tada se njegove dimenzije zanemaruju. I tijelo se pretvara u materijalnu točku.

Drugi slijedi iz odsutnosti deformacija u tijelu tijekom njegovog kretanja. Ili čak i tako beznačajne veličine, koje se mogu potpuno zanemariti.

Što je translacijsko kretanje tijela?

Za pojašnjenje, trebat ćete razmotriti bilo koje dvije točke unutar krutine. Oni trebaju povezati segment. Ako ovaj segment ostane paralelan početnom položaju tijekom kretanja, tada se kaže da je to kretanje naprijed.

Ako postoji zanemarivanje veličine tijela i smatra se materijalna točka Ovaj segment je odsutan i kreće se duž same linije.

Živopisni primjeri takvog pokreta

Prvo što treba zapamtiti je automobil za dizala. To savršeno ilustrira kretanje tijela naprijed. Dizalo se uvijek kreće isključivo gore ili dolje bez ikakve rotacije.

Sljedeći primjer koji ilustrira translacijsko gibanje je kretanje kabine Ferrisovog kotača. Međutim, ovo je stvarno samo u situaciji u kojoj se blagi nagib kabine na početku svakog pomaka ne uzima u obzir.

Treća situacija, kada je moguće govoriti o kretanju naprijed, povezana je s kretanjem pedala za bicikl. Njihovo kretanje se smatra relativno u odnosu na okvir. I ovdje se uvodi pretpostavka da se noge osobe ne ljuljaju dok jašu.

Popis se može dovršiti pomicanjem klipova koji osciliraju unutar cilindara motora s unutarnjim izgaranjem.

Glavni koncepti

Kinematika translacijskog gibanja je da proučava i opisuje kretanje krutih i materijalnih točaka. Međutim, ona ne uzima u obzir razloge koji prisiljavaju tijelo na to. Kako bi opisali kretanje, koordinate će biti potrebne da označe svoj položaj u prostoru. Osim toga, potrebno je poznavanje brzine i to u bilo kojem trenutku.

Prvo, vrijedi se sjetiti putanje. To je linija po kojoj se tijelo kretalo.

Prvi je ulazak u potez. To je vektor koji je označen s latinskim slovom r. Može povezati podrijetlo s položajem materijalne točke. U drugim slučajevima, ovaj vektor je nacrtan od početne do krajnje točke putanje. Jedinice pomaka su metri.

Druga vrijednost koja zaslužuje pozornost je put. Ona je jednaka dužini putanje kojom se tijelo pomiče. Put je označen slovom latinica S, koji se također mjeri u metrima.

Osnovne formule

Sada je vrijeme za brzinu. Ona je također vektor. Štoviše, ona karakterizira ne samo smjer kretanja tijela, već i brzinu njegovog kretanja. Vektor brzine je uvijek usmjeren duž tangentne linije, koja se može povući u bilo koju točku putanje. Označava se slovom V. Jedinice njezina mjerenja su m / s.
Brzina u svakom trenutku pokreta može se definirati kao derivat kretanja tijekom vremena. Ako je problem u pitanju ravnomjerno kretanje, tada vrijedi sljedeća formula:

• V = S: t, gdje je t vrijeme kretanja.

U situaciji u kojoj se smjer kretanja mijenja, morate koristiti zbroj svih pokreta.

Sljedeća vrijednost je ubrzanje. Opet, vektorska količina, koja je usmjerena prema brzini s velikom vrijednošću. Definiran je kao prvi derivat brzine tijekom vremena. Prihvaćena oznaka - slovo "a". Dimenzija je naznačena u m / s ² .

Formule za svaku komponentu ubrzanja, usmjerene duž osi, izračunate su kao omjer promjene brzine na toj osi i vremenskog intervala. Ako napravite matematički zapis, dobit ćete sljedeće:

• i _x = xV _x : .t.

Za projekcije ubrzanja na druge osi, formule su slične.
Osim toga, pri razmatranju kretanja duž putanje s zavojima, moguće je razgraditi vektor ubrzanja u dva termina:

• a = a _t + a _n , gdje je _t tangencijalno ubrzanje usmjereno duž tangente savijanja, a _n je normalno, što ukazuje na središte zakrivljenosti.

Prevodno gibanje bilo kojeg čvrstog tijela svodi se na opisivanje kretanja samo jedne njegove točke. Formule koje se koriste su:

• S = S ₀ + V ₀ t + (u ² ): 2.
• V = V ₀ + na.

U ovoj formuli indeksi "nula" označavaju početne vrijednosti količina.

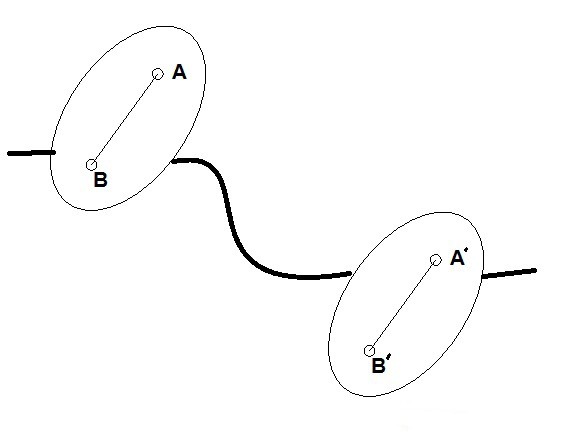
Teorem o translacijskoj veličini

Njegova formulacija je sljedeća: putanja, brzina i ubrzanje svih točaka tijela jednaki su tijekom kretanja naprijed.

Da biste to dokazali, morate napisati formulu vektorski dodaci pomak i vektor koji povezuje dvije proizvoljne točke. Trajektorije svih točaka dobivene su zbog njihovog prijenosa duž drugog vektora. I ne mijenja smjer i veličinu tijekom vremena. Stoga se može tvrditi da se sve točke tijela kreću istim putanjama.

Ako uzmemo derivat vremena, dobivamo vrijednost brzine. Štoviše, izraz je pojednostavljen do te mjere da su brzine dvije točke jednake.
Polje drugog derivata vremena je rezultat jednakosti ubrzanja dviju točaka.