Koje je područje matematike? Jedinice površine

Ima li problema s elementarnom geometrijom? Ovaj članak će vam pomoći riješiti jedan od njih. Ovdje ćete saznati što je to područje u matematici, o mjernim jedinicama i drugim važnim aspektima ove teme. Analiza nekih konkretnih primjera pružit će vam priliku da dodatno istražite problem.

Koje je područje matematike?

Područje je mjera koliko prostora ima na ravnoj površini. Na primjer, postoje dva identična komada papira, čija je ukupna površina očito veća od svake pojedinačno.

Područja likova u matematici izračunavaju se na različite načine, ovisno o njihovoj formi. Na primjer, u slučaju pravokutnika, morate pronaći proizvod njegove visine i širine. Pogledajmo sliku.

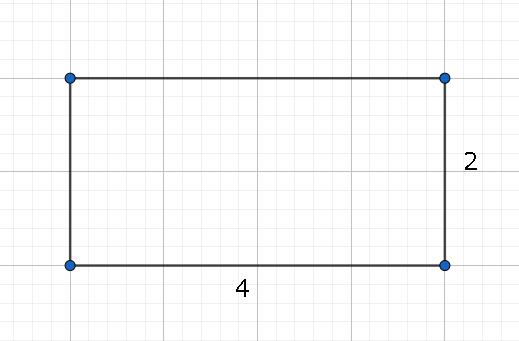
Imamo odgovor: 2 × 4 = 8 cm2. Problem riješen.

Možete ga provjeriti ručno brojanjem velikih kvadrata unutar pravokutnika. Takav zadatak je dovoljan da objasni što je područje u matematici. Ali u ovoj temi postoje i druge važne nijanse.

Jedinica mjerenja površine u matematici

Površina se mjeri u kvadratnim jedinicama. To jest, može se definirati kao određeni broj četverokuta čije su stranice jednake 1. U ovom slučaju, ako zamijenite vrijednosti duljine i visine, konačni rezultat se neće promijeniti.

NAPOMENA! Sve vrijednosti moraju biti u istim jedinicama.

Pretpostavimo da su podaci dani u centimetrima. Kako ga onda ispravno označiti na papiru?

Umjesto pisanja "osam četvornih centimetara", možete koristiti unos "8 cm ² ". Dovoljno je samo izgraditi reducirani oblik mjere na drugi stupanj.

Pretvorba vrijednosti

Student ili učenik možda će morati pretvoriti vrijednost iz jedne mjerne jedinice u drugu. Postoji samo jedan siguran način za to. Istina, za to je potrebno zapamtiti kako pravilno pretvoriti jednu mjernu jedinicu u drugu.

Pretpostavimo da imamo 9000 m ² . Moramo pronaći koliko hektara. Poznato je da 1 ha = 10 000 m ² . Podijelite izvorno područje za deset tisuća. Kao rezultat toga dobivamo 0,9 ha. To će biti željena vrijednost. Glavno je imati informacije o odnosu između dvije količine.

A sada provjerimo.

Ostale brojke

Nažalost, pronaći područje nije uvijek dovoljno da pomnožimo dva broja. Situacije su različite. Radna formula za svaku od njih će se s vremena na vrijeme mijenjati. U nastavku su najčešće varijacije oblika.

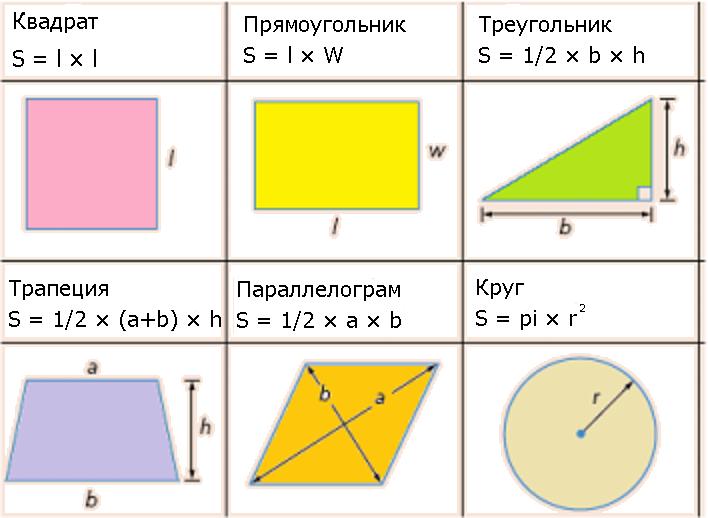
primjer

Sada znate što je kvadrat u matematici. Glavni teoretski materijal je naučen i možete nastaviti s praksom. Popraviti ćemo riješiti određeni problem.

Stanje. Tu je kvadrat sa stranom od 3 centimetra i krug s radijusom iste duljine. Pronađite čije je područje veće i koliko.

Odluka. Za početak ćemo izračune za svaku od pojedinosti izvršiti zasebno:

S _quad = 3 × 3 = 9. Dakle, kvadrat kvadrata je 9 cm2.

No, područje kruga izračunava se pomoću različite formule. Da biste ga pronašli, morate zapamtiti vrijednost ∏:

S _krug = ∏ × 3 × 3 ≈ 28,26 cm2.

Prema rezultatima, vidimo da je područje kruga nekoliko puta veće. Ostaje samo brojati koliko. Da biste to učinili, pronađite razliku između ta dva broja.

S _krug - S _quad = 28,26 - 9 = 19,26 cm2.

Odgovor je pronađen.

Obično, rješavajući takve probleme, osoba mora sve svesti na gotove formule. Potom potražite nepoznato, izrazite vrijednosti jedne kroz drugu i upotrijebite genijalnost.