Adijabatski proces, njegova suština i formule

Adijabatski proces (nazvan adijabatski u nekim izvorima) je termodinamički proces koji se odvija u odsutnosti razmjene topline s okolinom. Postoji nekoliko čimbenika koji karakteriziraju ovu klasu. Primjerice, adijabatski proces odvija se dinamički i postavlja se u kratkom vremenskom razdoblju. Postoje procesi ove klase, u pravilu, odmah.

Povezanost s prvim zakonom termodinamike

S njom se može izravno povezati adijabatski proces (adijabatski) prvi zakon termodinamike. Izraz "po defaultu" glasi kako slijedi: promjena količine topline u sustavu tijekom termodinamičkog procesa u njoj brojčano će biti jednaka zbroju promjene unutarnje energije idealnog plina i rada tog plina.

Ako pokušamo pisati prvi početak termodinamike u svom standardnom obliku dobivamo sljedeći izraz: dQ = dU + dA. I sada ćemo pokušati modificirati ovu formulu s obzirom na adijabatski proces. Kao što smo već spomenuli, takvi se procesi odvijaju pod uvjetom da nema razmjene topline s okolinom (vanjskim, kako to neki književni izvori nazivaju) medijem.

U ovom slučaju, formula koja opisuje prvi zakon termodinamike ima sljedeći oblik: dA = -dU. Sada malo više o izmjenama. Ako kažemo da nema izmjene topline u sustavu, promjena količine topline (naznačena u formuli prvog zakona termodinamike od strane dQ) bit će nula. Prema tome, jedan od dodataka možemo prenijeti s desna na lijevo, nakon čega dobivamo formulu reduciranu na ranije opisani oblik.

Slijedi prvi zakon termodinamike za adijabatski proces

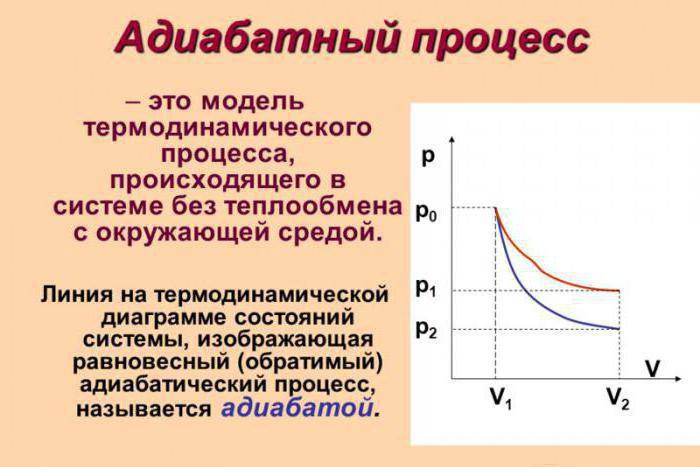
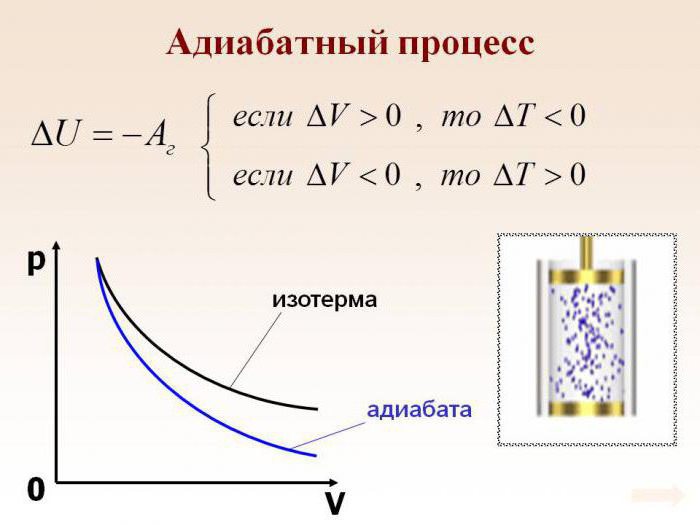
Pretpostavimo da je u sustavu došlo do adijabatskog procesa. U ovom slučaju, moguće je, bez ulaženja u najsitnije detalje, reći da plin radi tijekom ekspanzije, ali istovremeno gubi svoju unutarnju energiju. Drugim riječima, rad tijekom adijabatskog širenja plina provodit će se zbog gubitka unutarnje energije. Prema tome, kao rezultat ovog procesa, razmotrit ćemo smanjenje temperature same tvari.

Apsolutno je logično pretpostaviti da će, ako je plin adiabatski komprimiran, njegova temperatura porasti. Lako je vidjeti da će se tijekom procesa promijeniti sve glavne karakteristike idealnog plina. Radi se o tlaku, volumenu i temperaturi. Stoga je ime adijabatskog procesa izoprocesa postalo gruba pogreška.

Adijabatski proces. formula

Formula dobivena iz prvog zakona termodinamike zapisana je ranije. Koristeći ga, lako možemo izračunati rad općenito, koji će plin raditi tijekom adijabatskog procesa. Kao što ste možda pogodili, učinit ćemo to uz pomoć integracije.

Dakle, da bismo dobili opću formulu za rad za x mola plina, integriramo izraz prvog zakona termodinamike za adijabatski proces. Sve ovo će izgledati ovako: A = - (integral) od dU. Otvorimo ovaj izraz, dobijemo: A = - xCv (integralni od T1 do T2) dT.

Sada kada smo integrali integral u konačni oblik, možemo ga pojednostaviti. Na izlazu dobivamo sljedeću formulu: A = - xCv (T2 - T1). Pa, posljednji korak bit će malo pojednostavljenje. Riješimo se minusa prije formule. Da bismo to učinili, napravimo malu permutaciju u zagradama, mijenjajući konačnu temperaturu s početnim mjestima. Kao rezultat dobivamo: A = xCv (T1 - T2).

Adijabatska jednadžba

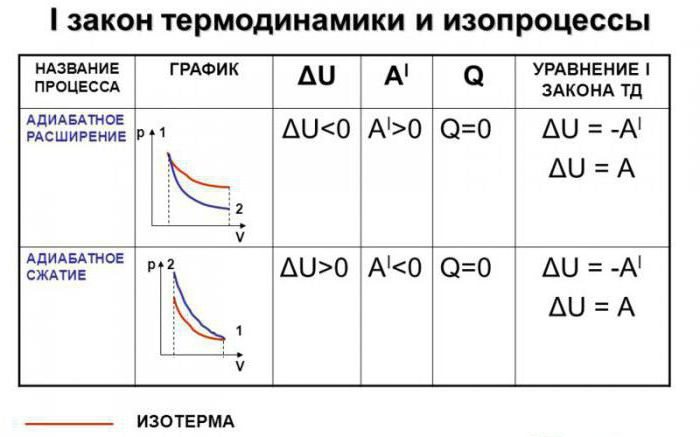
Koristeći prvi zakon termodinamike za adijabatski proces, možemo pronaći adijabatsku jednadžbu. Istodobno će se zabilježiti za proizvoljan broj molova idealnog plina. Dakle, zapisujemo izvornu formulu. Izgleda ovako: dA + dU = 0. No dobro znamo da je rad idealnog plina brojčano ništa više od produkta promjene tlaka i volumena.

Istodobno se mijenja unutarnja energija bit će jednaka radu sa suprotnim predznakom. I već smo je pronašli uz pomoć integracije. Dakle, prvi zakon termodinamike za adijabatski proces može poprimiti sljedeći oblik: pdV + xCvdT = 0. Moramo isključiti jedan pokazatelj iz ove jednadžbe, naime, temperaturu. Umjesto toga, njegove promjene. Da bismo to učinili, okrećemo se jednadžbi koja se često koristi u molekularnoj fizici. Naime, jednadžba Mendeljejev-Clapeyron.

Primarni izraz

Moramo ga razlikovati, što ćemo i učiniti. Dakle, općenito, jednadžba je sljedeća: PV = XRT. Zbog razlikovanja će se svesti na sljedeći oblik: pdV + Vdp = xRdT. Odavde možemo izraziti promjenu energije. Ona će biti jednaka lijevom dijelu podijeljenom s proizvodom količine tvari i univerzalne plinske konstante. Drugim riječima, formula bi bila: (pdV + Vdp) / xR. Ostaje samo da se pojednostavi. Kao rezultat, dobivamo sljedeći izraz: dT = (pdV + Vdp) / x (Cp - Cv)

Zapravo, prvi dio zadatka je završen. Ostaje samo da se sve privede na pamet.

Sekundarni izraz Zamjena vrijednosti

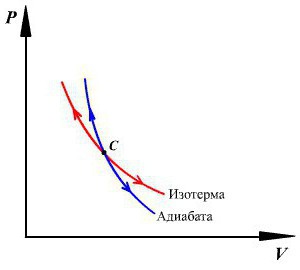
Uzmimo formulu Mendeljejev-Clapeyron dobivenu kao rezultat diferencijacije i zamijenimo je izrazom koji smo ranije izveli za prvi zakon termodinamike s obzirom na adijabatski proces. Što ćemo dobiti? Svi ovi glomazni izrazi imaju sljedeći oblik: pdV + xCv ((pdV + Vdp) / x (Cp-Cv)) = 0.

Da bismo sve to pojednostavili, moramo uzeti u obzir nekoliko činjenica. Prvo, izraz se može pojednostaviti reduciranjem na zajednički nazivnik. Kada dobijemo jednu frakciju, možemo upotrijebiti dobro staro pravilo, koje kaže da je frakcija nula kada je njezin numerator nula, a nazivnik nije nula. Kao rezultat kombinacije svih tih akcija, dobivamo sljedeći izraz: pCpdV - pCvdV + pCvdV + VCvdp = 0.

Sljedeći korak je podijeliti ovaj izraz na pVCv. Dobivamo zbroj dva dijela, dajući kao rezultat nulu. To će biti Cp / Cv * dV / V + dp / p = 0. Ova formula mora biti integrirana. Tada dobijemo sljedeći izraz: y (integralni) dV / V + (integralni) dp / p = (integral) 0.

Pa, onda je sve vrlo jednostavno. Koristeći formule za integraciju (integralni tablice mogu se koristiti za sve što je jednostavnije), završavamo sa sljedećim unosom: y ln V + ln p = ln (const). Ispada da je p (V) y = const. U molekularnoj fizici taj se izraz naziva Poissonova jednadžba. Mnogi znanstveni izvori tu formulu nazivaju i adijabatskom jednadžbom. Istodobno, vrijednost y, koja se pojavljuje u ovom zapisu, naziva se adijabatski indeks. Ona je jednaka (i + 2) / i. Valja napomenuti da je adijabatski indeks uvijek veći od jedan, što je u načelu logično.

Primjeri adijabatskih procesa

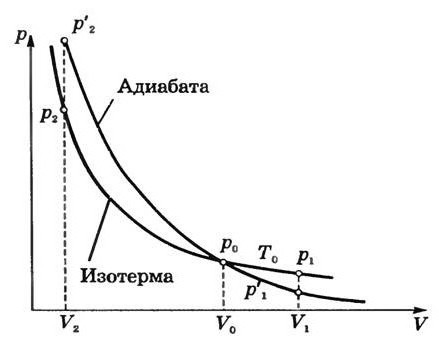
Ubrzo nakon što je otkriven adijabatski proces, započeo je veliki broj različitih studija. Tako je stvoren prvi teorijski model koji se odnosi na Carnotov ciklus. Ona je dopustila uspostavljanje uvjetnih ograničenja koja su ograničavala razvoj toplinskih motora. Ali u slučaju nekih stvarnih procesa koje treba provesti Carnotov ciklus dovoljno teško. Stvar je u tome što se sastoji od izotermi. A oni, zauzvrat, zahtijevaju određenu brzinu termodinamičkih procesa.

zaključak

Kako bi se izbjegli takvi problemi, osmišljen je Otto ciklus, kao i ciklus ukapljivanje plina. Postali su široko korišteni u rješavanju konkretnih problema u praksi. Početne studije pokazale su mogućnost opisivanja nekih prirodnih procesa u adijabatskom planu, što nam je omogućilo da identificiramo opće obrasce odgovarajućih procesa. Primjer adijabatskog procesa može se nazvati kemijskom reakcijom koja se događa unutar određenog volumena plina, ako je sustav zatvoren i nema razmjene topline s vanjskim okolišem.