Dirichletov princip: problemi s rješenjima
Postoji mnogo načela u matematici. Neki od njih su prilično jednostavni i razumljivi čak i za početnike, a neki zahtijevaju određena objašnjenja i dokaze. Međutim, svi su oni vrlo učinkoviti i mogu se lako primijeniti u praksi. Jedan od njih je Dirichletov princip (također poznat kao princip golub / zec). To je prilično jednostavna tvrdnja koja može pomoći u rješavanju mnogih matematičkih problema.

Povijest
Ovo načelo formulirao je počasni njemački matematičar Johann Dirichlet 1834. godine. Danas se koristi u kombinatorici, kao iu matematičkoj fizici. Prevedeno s izvornog njemačkog, zvuči kao "načelo kutija". Znanstvenik je proveo istraživanje s zečevima i spremnicima. Pokazao je da, ako stavimo, recimo, 5 zečeva u 7 spremnika, tada će barem u jednom spremniku biti 5/7 od jedne životinje. Međutim, kunić se ne može podijeliti na dijelove, stoga će barem jedna ćelija biti prazna (5/7 je 0 cijelih brojeva). Na isti način, u suprotnom smjeru, ako ima 7 kunića i 5 kutija, tada barem jedan od njih ima 2 kunića (7/5 je 2 netaknuta). Polazeći od te tvrdnje, matematika je uspjela formulirati princip koji već godinama osigurava uspješno rješavanje problema iz matematike.
Suvremeni tekst i dokaz
Danas postoji nekoliko različitih formulacija ovog načela. Najrazumljivije i najjednostavnije znači da je nemoguće posaditi 8 kunića u 3 kaveza tako da svaki ima više od 2. Znanstvenija i složenija formulacija koja objašnjava Dirichletov princip kaže: ako u k stanicama ima k + 1 kunića, tada barem Najmanje 1 ćelija sadržavat će više od jednog zeca. A ako u k stanicama ima k-1 zečeva, tada će najmanje 1 ćelija sadržavati manje od jednog zeca. Dokaz ove tvrdnje vrlo je jednostavan, da tako kažem, kontradiktornim. Ako pretpostavimo da je u svakoj ćeliji manje zeca od k-1 / k, onda je k zečjih stanica manji od k * k-1 / k = k-1, što je u suprotnosti s početnim uvjetima.
Zapravo, takav jednostavan i razumljiv princip uvelike olakšava rješavanje problema u matematici i dokaz mnogih teških teorema. Potrebno je samo uzeti u obzir da se zečevi i ćelije mogu lako zamijeniti matematičkim objektima i objektima (brojevi, točke, segmenti, brojke, itd.).
Još jedan tekst
Ponekad zadaci na Dirichletovom principu nisu tako jednostavni i očiti kao kod životinja u kutijama. To je načelo potrebno prenijeti na matematičke skupove kako bi se pronašla rješenja. U ovom slučaju, možete se osloniti na drugačiju, složeniju formulaciju. 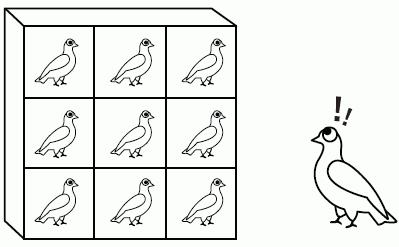
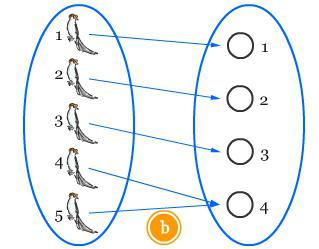
Ako mapiramo skup S koji sadrži d + 1 elemente u skup R s skupom elemenata d, tada će dva elementa iz skupa S imati istu sliku.
Iako moderni GEF u matematici nameće kreativne zahtjeve studentima i nudi nestandardne opcije, rješenje kroz Dirichletovu tvrdnju nije uvijek tako jednostavno i jednostavno. Ponekad je vrlo teško odrediti koju vrijednost treba smatrati životinjom, a koja kao kavez, te kako činjenica da imaju dvije životinje u jednom kavezu pomaže u rješavanju problema. A ako uspijemo to shvatiti, još je nemoguće odrediti u kojoj će se određenoj ćeliji nalaziti objekt. To jest, jednostavno možete dokazati postojanje takve ćelije, ali je ne možete konkretizirati.
Primjer broj 1. Geometrija
Moderni primjeri rješavanja problema pokazuju da savršeni razni matematički objekti mogu djelovati kao životinje i stanice.
zadatak
Linija k prolazi kroz ravninu trokuta ABC, ali ne siječe niti jedan od njegovih vrhova. Potrebno je dokazati da ne može prijeći svoje tri strane.
odluka
Zamislite kako linija k dijeli trokut na dvije ravnine, nazovimo ih s1 i s2. Pretpostavljamo da su s1 i s2 otvoreni, tj. Da ne sadrže l. Sada je vrijeme da primijenimo Dirichletov princip. Zadaci s rješenjima mogu pokazati da u suvremenim uvjetima zečevi i stanice označavaju različite objekte. Dakle, umjesto zečeva, zamjenjujemo vrhove trokuta, a umjesto ćelija poluplanu. Budući da nacrtana linija k ne siječe niti jedan od vrhova, svaki od njih je u jednoj ili drugoj ravnini. Ali budući da u trokutu postoje tri vrha i imamo samo dvije ravnine (s1 i s2), jedna od njih će sadržavati dva vrha. Pretpostavimo da su to vrhovi A i B i da su u polu ravnini s2 (to jest, leže na istoj strani k). U ovom slučaju, segment AB ne siječe pravac k. To jest, postoji strana u trokutu da se k ne siječe.
Alternativno rješenje
U ovom problemu pretpostavili smo da su točke A i B u istoj ravnini, ali Dirichletov princip ne ukazuje na specifičnu ćeliju, tako da možemo istaknuti da su točke C i B, ili A i C bile smještene u istoj ravnini. nije bitno koja strana trokuta ima ravnu crtu k. Stoga je ovaj princip idealan za njegovo rješavanje.
Primjer br. 2. Geometrija
zadatak
U sredini jednakostraničnog trokuta ABC (u kojem je AB = BC = AC = 1) pronađeno je 5 točaka. Potrebno je dokazati da se dvije nalaze na udaljenosti manjoj od 0,5.
odluka
Ako nacrtate srednje crte u desnom ABC trokutu, oni ga dijele na 4 mala pravokutna trokuta sa stranama ½ = 0.5. Pretpostavimo da su ti trokuti stanice, a točke unutar njih su zečevi. Pokazalo se da imamo 5 zečeva i 4 stanice, tako da će u jednom od njih biti najmanje dva zeca. S obzirom da točke nisu vertices (budući da se nalaze unutar trokuta ABC, a ne na jednoj od njegovih strana), oni će biti smješteni unutar malih figura. Zbog toga će udaljenost između njih biti manja od 0,5 (budući da veličina segmenta unutar trokuta nikada ne prelazi veličinu njegove najveće strane).
Primjer broj 3. Kombinatorika
U drugim poljima, također se može uspješno primijeniti Dirichletov princip: kombinatorika i matematička fizika na njoj se već dugo temelje pri rješavanju problema.
zadatak
Na primjer, oko zaokruženog stola, m zastave različitih zemalja stoje na jednakim međusobnim udaljenostima, a za stolom sjede predstavnici iz svake zemlje, a svaki od njih nalazi se pored tuđe zastave. Potrebno je dokazati da će uz određenu rotaciju stola barem dva predstavnika biti blizu svojih zastava.
odluka
Ispada da postoje načini m-1 za proširenje stola, tako da se mijenja međusobni raspored predstavnika i zastava (ako isključimo početni položaj tablice), ali ostaje m zastupnika.
Primjenjujemo Dirichletovu tvrdnju na rješenje i označavamo da su predstavnici zečevi, a određene pozicije tablica tijekom rotacije su stanice. U ovom slučaju, potrebno je napraviti analogiju između mjesta zastupanja pored odgovarajuće zastave i ispunjenih ćelija. To jest, pozitivan rezultat (jedan predstavnik je postavljen blizu njegove zastave) jednak je rezultatu "zec je u kavezu". Razumijemo da imamo jednu ćeliju manju od potrebne (m-1), što znači da će jedan od njih imati najmanje 2 zeca. Istovremeno, nisu isključene situacije da će neki kavez biti prazan (niti jedan predstavnik ne odgovara zastavi), ali u nekom kavezu će biti dva, tri ili čak više zečeva (dva, tri ili više predstavnika će se podudarati sa zastavama). Tako će se, uz određenu rotaciju, najmanje dva predstavnika naći u blizini svojih zastava (barem dva zeca će pasti u jednu ćeliju).
Započinjući rješavanje takvog problema, važno je razumjeti da je početna pozicija i ćelija, ali prema stanju problema očito je da je prazna, tako da ukupnu vrijednost smanjujemo za 1 (m-1).
Primjer broj 4. Teorija brojeva
Dirichletovo načelo u teoriji brojeva također je od najveće važnosti.
zadatak
Pretpostavimo, na komadu bilježnice u kavezu, učenik nasumce u čvorovima stanica stavi 5 bodova. Potrebno je dokazati da barem jedan segment s vrhovima u tim točkama prolazi kroz čvor stanice.
odluka
Prvo morate prikazati na listu bilježnice koordinatni sustav, čija se osnova nalazi u jednom od čvorova. Osi koordinatnog sustava podudaraju se s mrežnim crtama, a strana ćelije uzima se kao jedan segment. Ispada da će svih 5 označenih točaka biti u sustavu, a njihove koordinate će biti samo cijeli broj (parni ili neparni). Tako dobivamo 4 opcije koordinata: (parne, parne), (neparne, parne), (parne, neparne) i (neparne, neparne). Dakle, 2 od 5 bodova će odgovarati jednoj varijanti. Ako pogledate situaciju iz Dirichletovog položaja, onda morate odrediti točke kao zečeve, a opcije koordinata - kao ćelije. Dobivamo 5 ptica s jednim kamenom i 4 kaveza, u jednom od njih će biti najmanje 2 životinje. Pretpostavimo da su to točke P i A, s koordinatama (x 4 , y 3 ) i (x 5 , y 6 ). Sredina segmenta koji povezuje ta dva vrha će imati koordinate ((x 4 + x 5 ) / 2), ((y 3 + y 6 ) / 2)), koje će biti cijeli brojevi pod uvjetima odgovarajuće parnosti x 4 i x 5, y 3 i y 6 . Ispada da je sredina segmenta smještena u čvoru stanice.
Primjer broj 5
Dosta zadataka različite složenosti može se riješiti Dirichletovim načelom. Problemi s rješenjima različitih matematičkih i logičkih pitanja često se oslanjaju na to načelo.
zadatak
Na ravnoj cesti iskopali su male poprečne brazde. Razmak između svih žljebova jednak je i jednak Ö2 m. Potrebno je dokazati da, bez obzira na širinu utora, osoba koja hoda cestom u razmacima od 1 m jednom će pasti u jednu od njih.
odluka
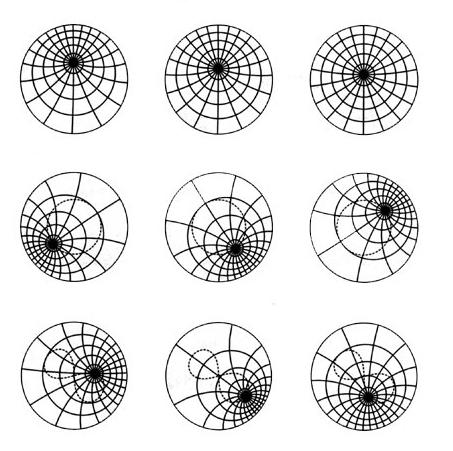
Kako bi se olakšalo rješenje, potrebno je zamisliti da se cesta može "namotati" na krug dužine Ö2 metra. Ispostavlja se da će se svi žljebovi spojiti u dva suprotna, a koraci osobe će biti prikazani u obliku luka jednake 1 m. Moramo sukcesivno označiti sve korake sve dok jedan od njih ne bude u luku koji označava utor, bez obzira na dužinu k luk (širina utora). Naravno, očito je da ako je čovjek prošao udaljenost jednaku manje od k, prije ili kasnije on bi ušao u jarak. Naposljetku, osoba ne može prijeći udaljenost k ako je duljina koraka manja od k. Dakle, trebamo pronaći dvije staze, udaljenost između kojih neće premašiti vrijednost k. Da bi to učinili, bilo bi prikladno koristiti načelo Dirichletova. Mi mentalno dijelimo cijeli krug na lukove veličine manje od k i smatrat ćemo ih kao stanice. Pretpostavimo da ih nema. Pretpostavimo da je broj koraka veći od broja lukova (n + m), iako se ne mogu podudarati dva koraka zbog iracionalnosti broja Ö2, tada će prema načelu Dirichlet barem jedna od stanica sadržavati više od jednog koraka. A budući da je dužina luka manja od k, tada će udaljenost između koraka biti manja. Stoga smo pronašli korake potrebne za dokaz. 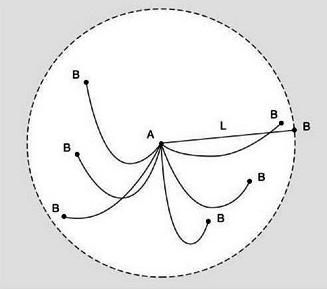
Generalizacija načela
Materijali o matematici, uz standardne (jednostavne i ne baš) formulacije, također sadrže jednu generaliziranu, koja se koristi za identificiranje više od dvaju sličnih objekata. Ona tvrdi da ako su dm + 1 kunići smješteni u d stanice, tada će najmanje m + 1 kunića biti u istoj stanici.
Primjer br. 6. Generalizacija
zadatak
Pravokutnik s površinom od 5 x 6 ćelija (30 ćelija), osjenčan samo 19. Je li moguće pronaći kvadrat s površinom od 2 x 2 ćelije u kojoj će najmanje tri biti obojane?
odluka
Naš lik mora biti podijeljen u 6 blokova od 5 ćelija. Na temelju izjave Dirichletova, barem 4 stanice će biti oslikane u jednoj od njih (19/6 = 4). Zatim u jednom od kvadrata s površinom od 4 ćelije, smještene u jednom od blokova, bit će obojano najmanje 3 stanice.
Primjer broj 7
Razred u kojem 25 ljudi. Od 3 slučajno odabrana studenta, dva će biti prijatelji. Potrebno je dokazati da u razredu postoji učenik koji ima više od 11 prijatelja.
Dva rješenja

Za početak, uzimamo dvoje školaraca koji nisu međusobno prijateljski raspoloženi (budući da su, ako su svi bili prijatelji jedni s drugima, u svakoj trojici bili tri prijatelja, a svaki bi učenik bio prijatelj s još 24 osobe). Preostalih 23 kolege će se družiti s jednim od nas dvojice, jer bi inače postojala trojka bez prijatelja (a to je u suprotnosti s izvornim stanjem problema). Ispada da će jedan od dva studenta biti prijatelj s najmanje 12 učenika. U ovom slučaju, učenici su zečevi, a izrazi "prijatelji ili ne" su stanice. Imamo 23 životinje i samo 2 kaveza. Prema tome, u jednom od njih najmanje 23/2 = 11,5, odnosno 12 zečeva. Odnosno, jedan od 2 izabrana studenta bit će prijatelji s najmanje 12 svojih kolega iz razreda (ili čak više). Naravno, postoje i drugi načini rješavanja problema, ali to je jedan od najrazumljivijih i najpogodnijih.