Četiri formule pomoću kojih možete izračunati površinu romba. Dijamantna svojstva

Romb je posebna figura u geometriji. Zbog svojih posebnih svojstava ne postoji jedna, već nekoliko formula pomoću kojih se izračunava površina romba. Koja su to svojstva i koje su najčešće formule za pronalaženje područja ove figure? Da vidimo.

Koji geometrijski oblik zove se dijamant

Prije nego što saznate što je područje romba, vrijedi znati kakva je to figura.

Od vremena euklidske geometrije, romb se naziva simetrični četverokut, čije su sve četiri strane jednake jedna drugoj u dužini i paralelne u parovima.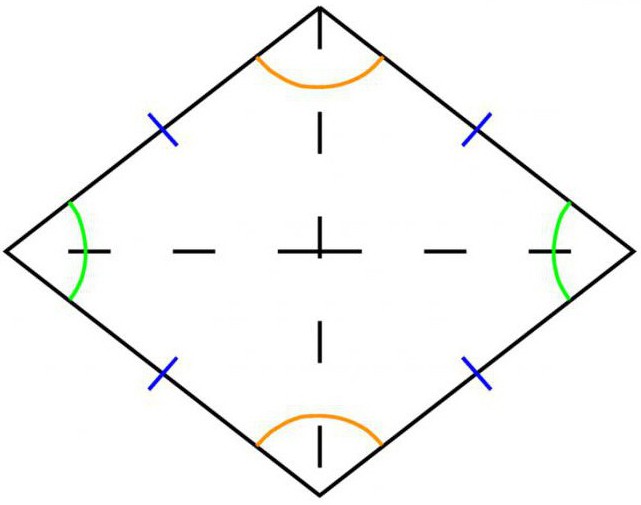

Podrijetlo izraza

Ime ove figure došlo je do najsuvremenijeg jezika iz grčkog, posredstvom latinskog. "Preteča" riječi "romb" postala je grčka imenica μόμβος (tamburina). Iako su stanovnici dvadesetog stoljeća, navikli na okrugle tamburine, teško zamisliti ih drugačijeg oblika, ali Heleni su tradicionalno te glazbene instrumente učinili neokruglim, već dijamantnim.

U većini suvremenih jezika ovaj se matematički pojam koristi, kao na latinskom jeziku: rombus. Međutim, na engleskom jeziku dijamanti se ponekad nazivaju dijamantom (dijamant ili dijamant). Taj je lik dobio takav nadimak zbog svog posebnog oblika, nalik dragocjenom kamenu. U pravilu se takav izraz ne koristi za sve dijamante, već samo za one čiji je kut presjeka između dviju strana šezdeset ili četrdeset pet stupnjeva.

Prvi put se ta brojka spominje u spisima grčkog matematičara, koji je živio u prvom stoljeću nove ere - čaplju Aleksandrije.

Koja svojstva ima ta geometrijska figura?

Da biste pronašli područje romba, najprije morate znati koje značajke ima ova geometrijska figura.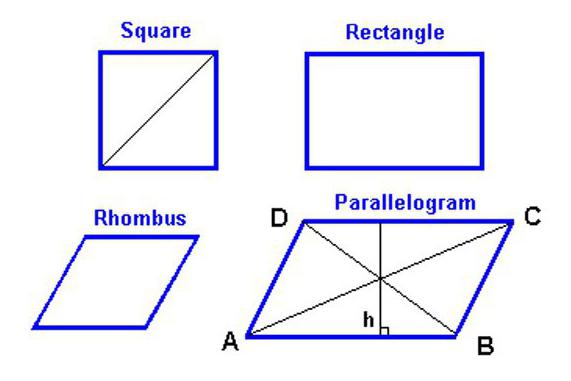

• Kao što je već spomenuto u definiciji romba, to je četverokut. I iz razloga što su njegove suprotne strane u parovima paralelne jedna drugoj, romb se također može nazvati paralelogram, što znači da se na njega odnosi većina svojstava ove figure.
• Oba dijagonalna romba na mjestu presjeka jednako su podijeljena na dva dijela. Zbog činjenice da se križaju pod kutom od devedeset stupnjeva, dijagonale dijele sliku na 4 pravokutni trokut.
• U svakom rombu dijagonale dijele kutove na dva dijela, a istodobno su i simetrali.
• Ako je svaka od dviju dijagonala romba podignuta na snagu kvadrata, tada će njihova suma biti jednaka proizvodu kvadrata na strani ove figure i broja četiri.
• Ako povežete crte sredine četiriju strana romba, rezultat će biti pravokutnik.
• Ako je kružnica upisana u dijamant (bez obzira na kutove), tada će se njezina središnja točka podudarati s središtem presjeka dijagonala.
• Dijagonalni dijamanti u dodiru s osima svoje simetrije na kutovima od devedeset stupnjeva.
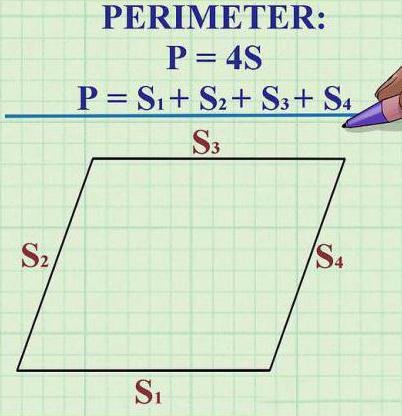
• Budući da su sve strane rombova međusobno identične po duljini, njegov se perimetar izračunava po formuli P = 4 x K (K je dužina jedne od strana).

Pod kojim uvjetima je paralelogram dijamant

Kao što znate, svaki romb je paralelogram, ali nije svaki paralelogram romb. Da bi se točno tvrdilo da je prikazana figura doista romb, a ne jednostavni paralelogram, ona mora odgovarati jednoj od tri glavne značajke koje razlikuju romb. Ili sve tri odjednom.

1. Dijagonalni paralelogram presijeca se pod kutom od devedeset stupnjeva.
2. Dijagonale dijele kutove na dva dijela, djelujući kao simetrali.
3. Ne samo paralelne, nego i susjedne strane imaju istu dužinu. To je, uzgred, jedna od glavnih razlika između romba i paralelograma, budući da druga figura ima samo paralelne strane, ali ne i susjedne.

Pod kojim uvjetima je kvadrat romb

Prema svojim svojstvima, u nekim slučajevima romb može istovremeno postati trg. Da biste jasno potvrdili tu tvrdnju, jednostavno okrenite trg u oba smjera za četrdeset pet stupnjeva. Dobivena figura će biti dijamant, svaki od kutova koji je devedeset stupnjeva.

Također, da biste potvrdili da je kvadrat romb, možete usporediti znakove tih figura: u oba slučaja, sve strane su jednake, a dijagonale su bisektrike i sijeku se pod kutom od devedeset stupnjeva.

Kako pronaći područje romba koristeći njegove dijagonale

U modernom svijetu na internetu možete pronaći gotovo sve materijale za obavljanje potrebnih izračuna. Dakle, postoji masa resursa opremljenih programima za automatski izračun površine određenog oblika. Štoviše, ako (kao u slučaju romba) postoji nekoliko formula za to, onda postoji mogućnost da odaberete koji od njih je najpogodniji za korištenje. Međutim, prije svega, potrebno je biti u stanju izračunati površinu romba bez pomoći računala i biti orijentiran u formulama. Za dijamant ima mnogo, ali najpoznatiji od njih su četiri.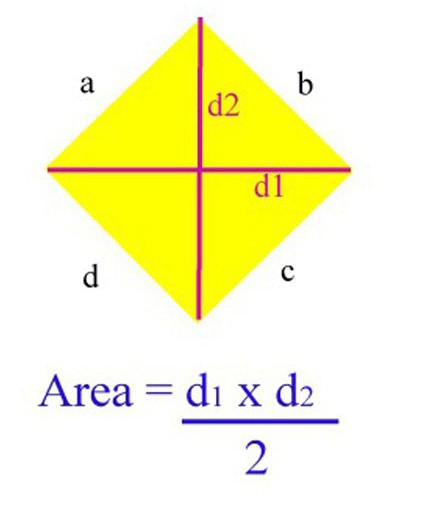

Jedan od najjednostavnijih i najčešćih načina otkrivanja područja ove figure, ako postoje informacije o duljini njegovih dijagonala. Ako problem ima ove podatke, u ovom slučaju možete primijeniti sljedeću formulu kako biste pronašli područje: S = KM x LN / 2 (KM i LN su dijagonala KLMN romba).

U praksi možete provjeriti valjanost ove formule. Pretpostavimo da KLMN romb ima jednu dijagonalu KM, njegova duljina je 10 cm, a druga LN 8 cm, a zatim te podatke zamijenimo gornjom formulom i dobijemo sljedeći rezultat: S = 10 x 8/2 = 40 cm2.

Formula za izračun površine paralelograma

Postoji još jedna formula. Kao što je već spomenuto u definiciji romba, ona nije samo četverostrana, već i paralelogram i ima sve značajke tog oblika. U ovom slučaju, da bi se pronašlo njegovo područje, razumno je koristiti formulu koja se koristi za paralelogram: S = KL x Z. U ovom slučaju, KL je duljina paralelograma (romb), a Z je dužina visine povučene na ovu stranu.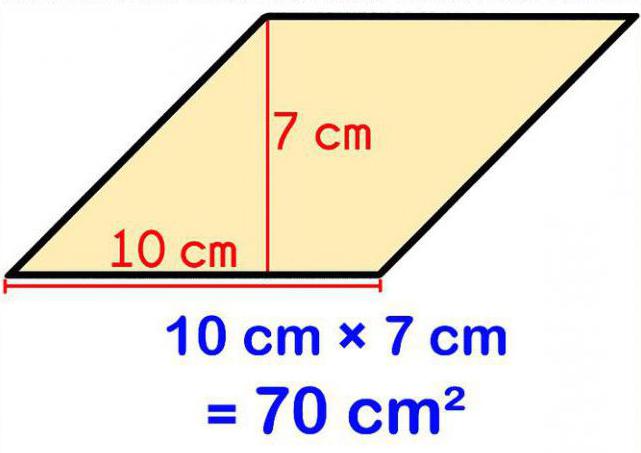

U nekim zadacima nije dano duljina stranice, ali je poznat perimetar dijamanta. Budući da je formula za pronalaženje bila naznačena gore, može se upotrijebiti za utvrđivanje duljine stranice. Dakle, perimetar je 10 cm, a duljina bočne strane može se prepoznati obrtanjem perimetralne formule i podjelom 10 na 4. Rezultat će biti 2,5 cm - to je željena dužina rombove strane.

Sada je vrijedno pokušati zamijeniti taj broj u formuli, znajući da je duljina na strani također 2,5 cm, a sada ćemo pokušati staviti te vrijednosti u gore navedenu formulu paralelograma. Pokazalo se da je površina romba S = 2,5 x 2,5 = 6,25 cm2.

Ostali načini izračunavanja dijamantnog područja

Oni koji su već ovladali sinusima i kosinusima mogu koristiti formule koje ih sadrže kako bi pronašli područje romba. Klasičan primjer je sljedeća formula: S = KM ² x Sin KLM. U tom slučaju, područje figure je jednako produktu dviju strana romba pomnoženo s sinusom kuta između njih. Budući da su sve strane jednake u rombu, lakše je odmah proizvesti jednu stranu u kvadrat, kao što je prikazano u formuli.

Ovu shemu provjeravamo u praksi, a ne samo na rombu, već na kvadrat, koji, kao što je dobro poznato, ima sve kutove ravne, što znači da su devedeset stupnjeva. Pretpostavimo da je jedna od strana 15 cm, a poznato je i da je sinus kut od 90 ° jedan. Zatim, prema formuli, S = 15 x 15 x Sin 90 ° = 255x1 = 255 cm2 ^.

Osim gore navedenog, u nekim slučajevima, koristi se i druga formula koja koristi sinus za određivanje površine romba: S = 4 x R ² / Sin KLM. U ovoj varijanti koristi se polumjer kružnice upisane u dijamant. Ona se uzdiže do kvadrata i množi se s četiri. I cijeli rezultat je podijeljen sinusom kuta koji se nalazi uz upisanu sliku.

Primjerice, za jednostavnost izračuna ponovno ćemo uzeti kvadrat (sinus njegovog kuta uvijek će biti jednak jednom). Polumjer kružnice ispisan u njemu iznosi 4,4 cm, a zatim se površina romba izračunava na sljedeći način: S = 4 x 4,4 ² / Sin 90 ° = 77,44 cm ²

Navedene formule za pronalaženje radijusa romba daleko su od jedine takve vrste, ali najlakše ih je razumjeti i provesti izračune.