Kako izračunati kutove između linije i ravnine?
Kada proučavamo školski tečaj geometrije u dvodimenzionalnom prostoru, mnogo vremena posvećujemo razmatranju ponašanja ravnih linija. Kad se okrenu studiju stereometrije u višim razredima, teme planova i ravnih linija u prostoru dolaze do izražaja. Ovaj se članak bavi jednim od ovih pitanja. Naime, tema izračunavanja između ravnina i pravih kutova i udaljenosti.
Pravac na ravnini i metode za postavljanje
Da bi se uspješno riješili problemi računanja između ravnih linija i ravnina kutova i udaljenosti, potrebno je naučiti matematički postaviti te geometrijske objekte, te ovladati metodama rada s odgovarajućim jednadžbama. Počinjemo s navođenjem linija na ravnini.
Svaki student zna sljedeću formulu:
y = k * x + b
Rad s njim prilično je zgodan u dvodimenzionalnom prostoru. Lako se koristi za crtanje ravne crte u pravokutnom koordinatnom sustavu. Osim toga, poznavanje koeficijenta k za svaku od njih omogućuje nam da kažemo da li će biti paralelni, ili će se presjeći (za paralelno, njihovi koeficijenti k su jednaki).
Ako zadani izraz napišemo u nešto drugačijoj formi, dobivamo formulu općeg tipa za ravnu liniju. Njen oblik je sljedeći:
A * x + B * y + C = 0
Očito, koristeći jednostavne transformacije, možete dobiti prvi izraz iz njega.
Pisane formule mogu se koristiti i za izračun kuta presijecanja pravaca. Međutim, to zahtijeva brojne transformacije, što je nezgodno. Stoga, kada zadatak zahtijeva pronalaženje kuta, poželjno je koristiti vektorski oblik prikaza linije. Njezin pogled može biti napisan kao:
(x; y) = (x 0 ; y 0 ) + λ * (a; b)
U toj jednakosti koordinate X i Y s indeksima nula opisuju položaj neke točke kroz koju prolazi linija. Vrijednosti a i b su koordinate vektora koji leži na njemu. Može se usmjeriti kako u jednom smjeru ravno tako iu drugom, pravac se ne mijenja. Ovaj se vektor naziva vodeći vektor, jer jedinstveno određuje distribuciju ravne linije na ravnini. Lambda λ je parametar koji uzima proizvoljnu vrijednost iz skupa realnih brojeva.
Napominjemo da je vektorski oblik zapisa izvanredan, što jasno sadrži usmjereni segment ravne linije, čije se koordinate koriste za određivanje kuta između dviju ravnih linija na ravnini.
Ravna crta u trodimenzionalnom prostoru
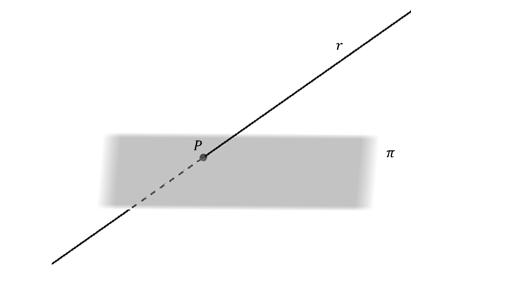
U prostoru opisanom s tri koordinatne osi pravac je općenito definiran kao sjecište ravnina. Ovdje, s obzirom na temu članka, razmatramo samo vektorsku jednadžbu. Sličan je onom za plosnati slučaj, ali s dodatkom treće koordinate:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a; b; c)
Pri rješavanju problema ovaj je izraz prikladan za otvaranje i primjenjivati u obliku parametara:
x = x 0 + λ * a;
y = y 0 + λ * b;
z = z 0 + λ * c
Napominjemo da će vrijednost parametra λ, iako arbitrarna, ovisiti za sve tri jednakosti.
Opis zrakoplova
Kao i za ravnu liniju, za ravninu postoje i brojni načini definiranja. Razmotrite samo dva od njih koja su važna da biste mogli riješiti probleme u praksi.
Prva metoda zadatka je donijeti jednadžbu općeg tipa. To je slično odgovarajućem izrazu za pravac u dvodimenzionalnom slučaju:
A * x + B * y + C * z + D = 0
Kombinacija prva tri koeficijenta su koordinate vektora pravca za tu ravninu. U pravilu, označen je simbolom n¯, to jest:
n¯ = (A; B; C)
Četvrti koeficijent D određuje udaljenost između paralelnih ravnina koje imaju prva tri jednaka koeficijenta.
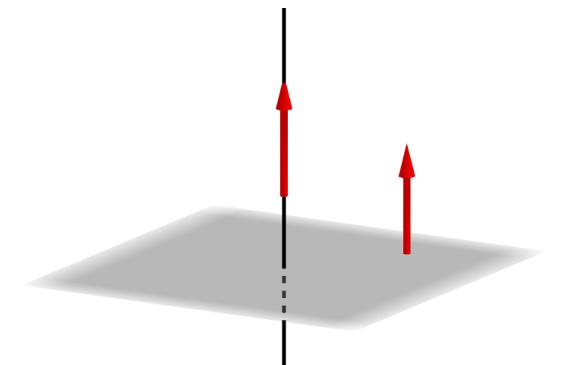
Budući da vektor np leži na normali na ravninu, on je okomit na apsolutno bilo koji vektor i pravac konstruiran na njegovim proizvoljnim točkama. Poznavanje koordinata n¯ je ključno pri određivanju između pravaca i kutova kuta.
Drugi način definiranja ravnine je vektorsko-parametarski oblik jednadžbe. Tako je napisano:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a 1 ; b 1 ; c 1 ) + γ * (a 2 ; b 2 ; c 2 )
Ta jednakost odražava činjenicu da dvije ravne linije jedinstveno definiraju ravninu u prostoru. Ovdje drugi i treći izraz označavaju dva smjera vektora za proizvoljne ravne linije koje pripadaju ravnini.
Normalni vektor n¯ nije eksplicitno sadržan za ovaj oblik pisanja, ali ga je lako izračunati:
n¯ = [(a 1 ; b 1 ; c 1 ) * (a 2 ; b 2 ; c 2 )]
Kut između ravnih linija
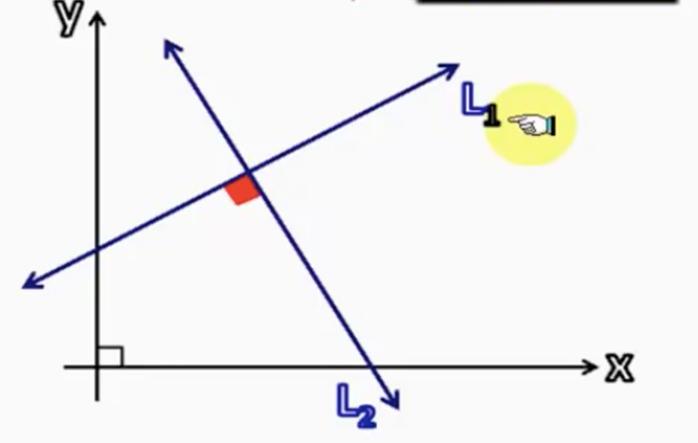
Ako su vektorske jednakosti za svaku od ravnih linija poznate, tada je kut između njih jednostavan. Da biste to učinili, trebate samo koristiti svojstva skalarnog proizvoda za segmente vodiča ravnih linija. Ako su vektorski vodiči označeni simbolima v¯ i u¯, tada će tražena formula poprimiti oblik:
α = arccos (| (v¯ * u¯) | / (| v¯ | * | u¯ |))
Budući da se u slučaju presjeka pravaca formiraju dva para jednakih kutova, tada se smatra da je akutni kut između njih. Iz tog razloga formula sadrži znak modula u brojniku.
Ova formula za dvodimenzionalni slučaj uvijek vrijedi. Rezultirajuća vrijednost od 0 o kaže da se prave crte ne sijeku, već su paralelne.
Što se tiče slučaja u prostoru, osim izračuna po formuli, potrebno je provesti dodatne izračune. Oni su povezani s pronalaženjem točke ukrštanja predmetnih objekata. Činjenica je da se u prostoru može dobiti konačna vrijednost kuta α, ali ravne linije neće se presijecati, budući da se mogu prelaziti.
Ravnina, linija i kut njihova raskrižja
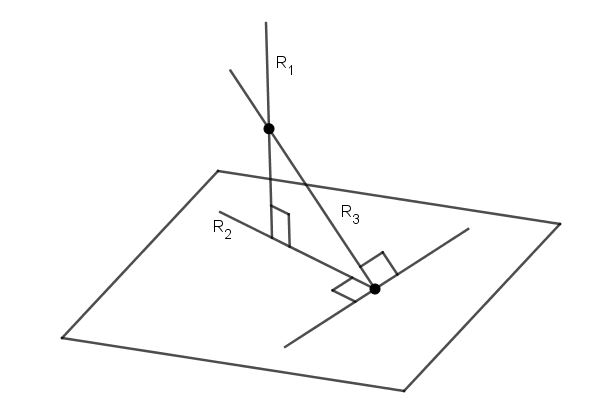
Da bismo pronašli kut između ravne linije i ravnine, dovoljno je znati jednadžbu za svaki od tih objekata. Kut između njih je kut dvaju presijecajućih linija, od kojih je jedan izvorni, a drugi pripada ravnini i predstavlja projekciju izvorne linije na nju. Na donjoj slici prikazana je ravnina u kojoj se pravac siječe pod kutom α.
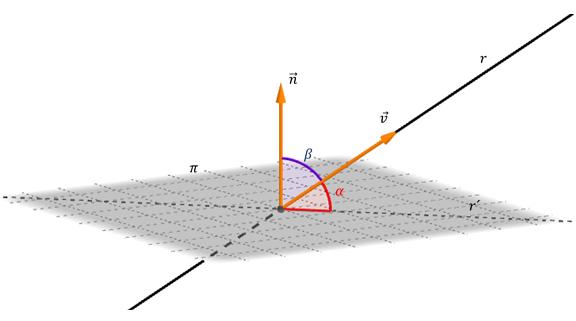
Ako je vektor usmjeravanja za direktni vektor označen s v¯, a norma ravnini je np (vidi sliku), tada izračun kuta α dobiva se formulom:
α = arcsin (| (v¯ * n¯) | / (| v¯ | * | n¯ |))
Napominjemo da se u ovoj formuli, za razliku od sličnog izraza za dvije linije koje se sijeku, koristi funkcija arcsine, a ne luk kosinusna funkcija.
Udaljenost između ravnih linija na ravnini i ravnine i ravne linije u prostoru
Za izračunavanje udaljenosti između predmetnih objekata u geometriji postoji skup formula. Primjena izraza iz njega ovisi o obliku u kojem su dane ravnina i linija.
Ako su dvije ravne linije dane u općem obliku na ravnini, tada se udaljenost između njih može izračunati na sljedeći način:
d = | A * x 1 + B * y 1 + C | / √ (A 2 + B 2 )
Ovdje x 1 i y 1 su koordinate proizvoljne točke na jednoj pravoj liniji, a koeficijenti A, B, C uzeti su za drugu ravnu crtu. Ova formula vrijedi ako su linije paralelne jedna s drugom. Ako se sijeku, udaljenost je nula.
Udaljenost između crte i prijelaza na ravnini je nula. Ako je pravac paralelan s ravninom, tada se odgovarajuća udaljenost izračunava kao:
d = | A * x 1 + B * y 1 + C * z 1 + D | / √ (A 2 + B 2 + C 2 )
Tamo gdje koordinate pripadaju proizvoljnoj točki na crti.
Zadatak: odrediti kut između ravne linije i ravnine
S obzirom na ravnu crtu i ravninu:
(x; y; z) = (1; 2; 0) + λ * (- 1; 1; 4);
-5 * x + y - 3 = 0
Koji je kut između ravne linije i ravnine?
Pišemo vodiče vektora v i np:
v = (-1; 1; 4);
n¯ = (-5; 1; 0)
Zamijenite ih odgovarajućom formulom za α, dobivamo:
α = arcsin (| 5 + 1 + 0 | / (*18 * √26)) ≈ 16,1 o
Zadatak: pronaći udaljenost između ravnih linija
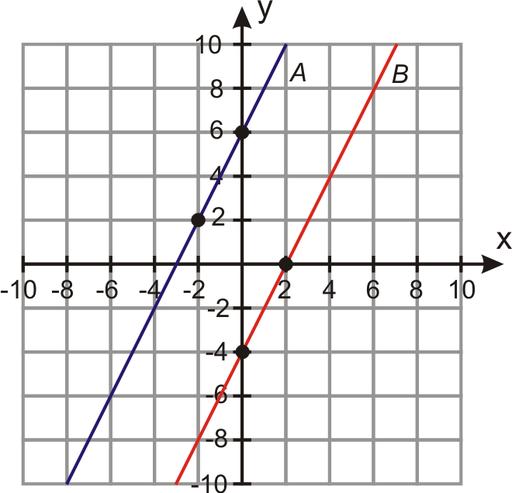
Dane su dvije jednadžbe pravaca u dvodimenzionalnom prostoru:
y = 3 x x - 1;
y = 3 x x 3
Kolika je udaljenost između njih?
Budući da su koeficijenti k za oba objekta isti (jednaki 3), događa se slučaj paralelnih pravaca.
Da biste izračunali udaljenost između njih, uzmite proizvoljnu točku prve ravne crte i napišite drugu jednadžbu općenito, imamo:
koordinate točke (0; -1);
3 * x - y + 3 = 0, to jest, A = 3, B = -1, C = 3
Sada se te vrijednosti mogu zamijeniti odgovarajućom formulom:
d = | 3 * 0 -1 * (- 1) + 3 | / √ (9 +1) = 4 / √10 ≈ 1.265
Odgovor se prima u jedinicama tog koordinatnog sustava.