Kako pronaći prave brojeve?

Brojevi su različiti: prirodni, prirodni, racionalni, cjelobrojni i djelomični, pozitivni i negativni, složeni i jednostavni, čudni i parni, stvarni, itd. Iz ovog članka možete saznati koji su jednostavni brojevi.

Koji se brojevi nazivaju engleska riječ "simpl"?

Vrlo često, studenti na jednom od najkompliciranijih pitanja na prvi pogled matematike, o tome što je glavni broj, ne znaju odgovoriti. Često brkaju jednostavne brojeve s prirodnim brojevima (tj. Brojeve koje ljudi koriste pri brojanju stavki, dok u nekim izvorima počinju od nule, u drugima - od jednog). Ali to su u potpunosti dvije različite stvari. Primarni brojevi su prirodni, tj. Cijeli brojevi i pozitivni brojevi, koji su veći od jednog i koji imaju samo 2 prirodna razdjelnika. U ovom slučaju, jedan od tih djelitelja je dani broj, a drugi je jedan. Na primjer, tri su prosti broj, budući da nije djeljiv ni s jednim drugim brojem osim s njim i drugim.

Složeni brojevi

Suprotno od primes je spoj. Oni su također prirodni, također više od jednog, ali nemaju dva, već veći broj razdjelnika. Na primjer, brojevi 4, 6, 8, 9 itd. Su prirodni, kompozitni, ali ne i prosti brojevi. Kao što možete vidjeti, to su uglavnom parni brojevi, ali ne svi. Ali "dva" - parni broj i "prvi broj" u nizu prostih brojeva.

sekvenca

Za izgradnju niza prostih brojeva, potrebno je napraviti izbor iz svih prirodnih brojeva, uzimajući u obzir njihovu definiciju, to jest, morate djelovati suprotno. Potrebno je razmotriti svako od pozitivnih cijelih brojeva kako bi se utvrdilo ima li više od dva razdjelnika. Pokušajmo izgraditi niz (slijed) koji čine prave brojeve. Popis počinje s dva, sljedeći je s tri, jer je podijeljen samo na sebe i na jedinice. Razmotrite broj četiri. Ima li razdvajače osim četiri i jedan? Da, ovaj broj je 2. Dakle, četiri nisu prosti broj. Pet je također jednostavan (nije djeljiv s drugim brojem osim 1 i 5), ali šest je djeljiv. I općenito, ako slijedite sve parne brojeve, možete vidjeti da osim za dva, nijedna od njih nije jednostavna. Odavde zaključujemo da čak i brojevi, osim dva, nisu jednostavni. Još jedno otkriće: svi brojevi koji se mogu podijeliti u tri, osim samog trijade, bilo da je paran ili neparan, također nisu jednostavni (6, 9, 12, 15, 18, 21, 24, 27, itd.). Isto vrijedi i za brojeve koji su podijeljeni u pet i sedam. Svi oni također nisu jednostavni. Sažetak. Dakle, jednoznamenkaste su sve neparnih brojeva osim jednog i devetog, a od parnog - samo "dva". Više desetaka (10, 20, ... 40, itd.) Nije jednostavno. Dvocifrene, troznamenkaste i tako dalje jednostavne brojeve može se odrediti na temelju gore navedenih načela: ako nemaju druge divizore osim sebe i one.

Teorije o svojstvima prostih brojeva

Postoji znanost koja proučava svojstva cijelih brojeva, uključujući primes. To je grana matematike, koja se naziva najviša. Osim svojstava cijelih brojeva, ona se također bavi algebarskim, transcendentalnim brojevima, kao i funkcijama različitog podrijetla povezane s aritmetikom tih brojeva. U ovim se studijama, pored elementarnih i algebarskih metoda, koriste i analitički i geometrijski. Naime, proučavanje prostih brojeva uključenih u teoriju brojeva.

Primarni brojevi su "građevni blokovi" prirodnih brojeva.

U aritmetici postoji teorem, koji se naziva glavni. Prema njemu, svaki prirodni broj, osim jednog, može se predstaviti kao proizvod čiji su faktori jednostavni brojevi, a redoslijed redoslijeda faktora je jedinstven, to znači da je način predstavljanja jedinstven. To se naziva dekompozicija prirodnog broja u proste faktore. Postoji još jedno ime za taj proces - faktorizacija brojeva. Polazeći od toga, jednostavni brojevi mogu se nazvati "građevni materijal", "blokovi" za izgradnju prirodnih brojeva.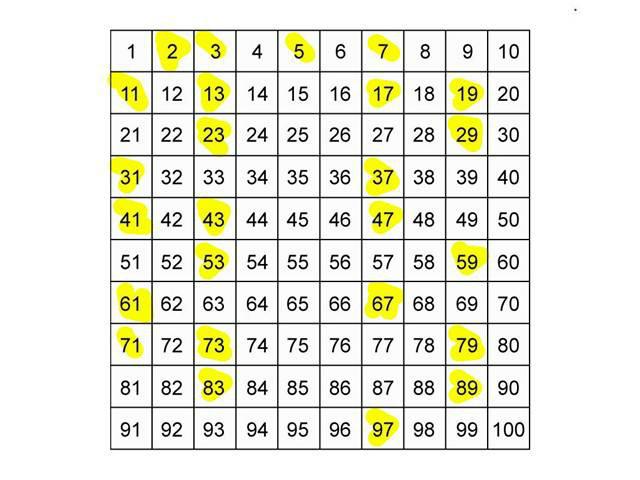

Tražite prave brojeve. Testovi jednostavnosti

Mnogi znanstvenici iz različitih vremena pokušali su pronaći neka načela (sustave) za pronalaženje popisa prostih brojeva. Znanost poznaje sustave koji se nazivaju Atkin sito, Sundartam sito i Eratostenovo sito. Međutim, oni ne daju nikakve značajne rezultate, a jednostavna provjera se koristi za pronalaženje primes. Također, matematičari su stvorili algoritme. Nazivaju se testovi jednostavnosti. Na primjer, Rabin i Miller su razvili test. Koriste ga kriptografi. Tu je i Kayal-Agraval-Sasken test. Međutim, unatoč dovoljnoj točnosti, vrlo je teško izračunati, što umanjuje njegovu praktičnu vrijednost.

Ima li skup prostih brojeva ograničenje?

Činjenica da je skup jednostavnih je beskonačnost, napisao je u knjizi "Principi" drevni grčki učenjak Euklid. Rekao je ovo: „Zamislimo na trenutak da primes ima granicu. Onda ih pomnožimo jedni s drugima i dodamo jedan proizvodu. Broj dobiven kao rezultat tih jednostavnih radnji ne može se podijeliti na jedan od brojnih prostih brojeva, jer će uvijek biti jedan u ostatku. A to znači da postoji neki drugi broj koji još nije uključen u popis prostih brojeva. Stoga, naša pretpostavka nije istinita, a taj skup ne može imati ograničenje. Uz dokaz Euclida, postoji i modernija formula koju je dao švicarski matematičar iz osamnaestog stoljeća Leonard Euler. Prema njegovim riječima, zbroj obrnut od zbroja prvih n brojeva raste bez ograničenja kako broj n raste. Ali formula teorema o raspodjeli primila: (n) raste kao n / ln (n).

Koji je najveći prost broj?

Svejedno je Leonard Euler uspio pronaći najveći premijer za svoje vrijeme. To je 2 ³¹ - 1 = 2147483647. Međutim, do 2013. izračunata je druga najtočnija u popisu prostih brojeva, 2 ^57885161-1 , koja se naziva Mersennov broj. Sadrži oko 17 milijuna decimalnih znamenki. Kao što možete vidjeti, broj koji su pronašli znanstvenici iz osamnaestog stoljeća je nekoliko puta manji od toga. Tako je i trebalo biti, jer je Euler ručno izračunavao, a naše računalo je vjerojatno pomoglo našim suvremenicima. Štoviše, taj je broj dobiven na matematičkom fakultetu na jednom od američkih fakulteta. Brojevi, nazvani po ovom znanstveniku, prolaze kroz Luke-Lemereov test jednostavnosti. Međutim, znanost ne želi tu stati. Electronic Frontier Foundation, koja je osnovana 1990. godine u Sjedinjenim Američkim Državama (EFF), imenovala je novčanu nagradu za pronalaženje velikih premijskih brojeva. A ako se do 2013. nagrada oslanja na one znanstvenike koji bi ih pronašli između 1 i 10 milijuna decimalnih brojeva, danas je ta brojka dostigla od 100 milijuna do 1 milijardu. Veličina nagrade kreće se od 150 do 250 tisuća američkih dolara.

Imena posebnih primes

Brojevi koji su pronađeni zahvaljujući algoritmima koje je stvorio jedan ili drugi znanstvenik i koji su prošli test jednostavnosti, nazivaju se posebnim. Evo nekih od njih:

1. Merssen.

2. Wooda.

3. Farma.

4. Cullen.

5. Prota.

6. Mills i sur.

Jednostavnost ovih brojeva, nazvana prema gore navedenim znanstvenicima, utvrđena je sljedećim testovima:

1. Luc-Lemer.

2. Pepin.

3. Rizel.

4. Billhart - Lemera - Selfridge itd.

Moderna znanost se tu ne zaustavlja i vrlo je vjerojatno da će u bliskoj budućnosti svijet znati imena onih koji bi mogli dobiti nagradu od 250.000 dolara, pronalazeći najveći premijerni broj.