Kako pronaći gcd od dva broja? "Turbo Pascal" i malo matematike

Često se početnički programeri upoznaju s Turbo Pascal okruženjem kroz jednostavne zadatke. Prvi zadaci koje korisnik implementira u kodu: prikazati bilo koji tekst, pronaći GCD i NOC prirodni brojevi izračunati koliko je četvrtina u mjesecu, itd. Često postoje zadaci s matematičkom predrasudom. Prije nego što implementirate svoje znanje u programski kod, potrebno je proučiti dodatni materijal. Na primjer, kako pronaći GCD i NOC od dva broja u Turbo Pascalu.

Pronalaženje gcd u matematici

Najveći zajednički faktor je broj koji se smatra maksimalnim kada se raspadne na komponente. Snimljen je kratki oblik definicije kao GCD. Na primjer, razmotrite crtež. Ovdje su dani brojevi 140 i 175. Njihov najveći djelitelj je 35, odnosno GCD (140.175) = 35.

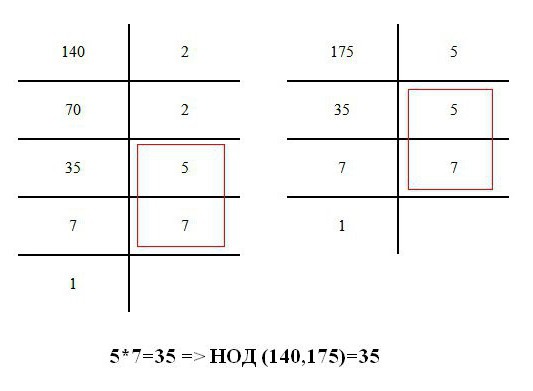
Da biste izbjegli dodatna pitanja o tome kako pronaći GCD dva broja, trebate slijediti ovaj algoritam:

• Nađite najjednostavnije djelitelje prvog broja.
• Ista operacija se radi s drugim brojem.
• Pronaći zajedničke pokazatelje u skupu razdjelnika prvog i drugog broja.
• Zaokružite ih olovkom druge boje.
• Pomnožite zajedničke razdjelnike (ako ih je više) ili ispišite samo jednu (ako brojevi su primarni tada će njihov gcd biti jednak 1).

Razmotrite sljedeću sliku. To pokazuje da čak i tako veliki brojevi kao 816 i 455 nemaju GCD, osim za 1.

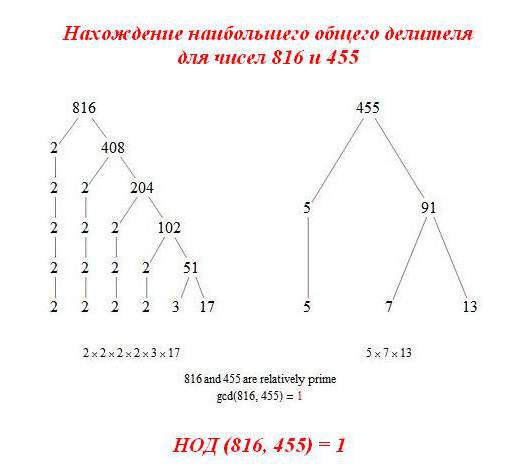
Postoji drugi način za pronalaženje zadatka. Euklidski algoritam u matematici je sljedeći:

• S obzirom na brojeve.
• Odabir bi trebao biti maksimalan.
• Podijeljen je na minimum.
• Sada drugi navedeni broj mora biti podijeljen s rezultirajućim saldom.
• Prva bilanca se dijeli s drugom, koja proizlazi iz prethodne operacije.
• Drugi rezidualni dio podijeljen je s trećim itd.
• Operacija podjele provodi se dok ostatak ne bude jednak 0.
• Posljednji razdjelnik i ispunjava kriterij NOD.

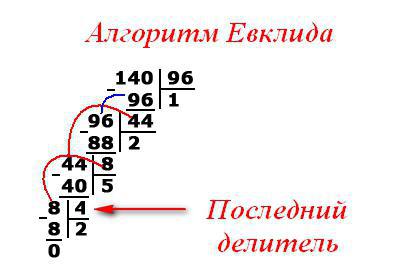
Da bi pronašli GCD više od tri prirodna broja, preporuča se slijediti shemu rada (uzmi brojeve 140, 96, 64):

• U prvom koraku ponovite gornji algoritam za prva dva broja.
• Pronađite GCD pronađenog djelitelja i dani treći broj.
• Pronađite GCD rezultirajućeg djelitelja i četvrtog broja, itd.

Pronalaženje NOC-a iz matematike

Ako se programiranjem postavlja pitanje kako pronaći GCD dva broja, onda je on nužno povezan s drugim: nalaz NOO-a. Najmanje zajedničko više od dva broja je takav minimalni prirodni broj koji se može dijeliti s prvim i drugim brojem.

Prvi način:

• S dva ili više brojeva.
• Napišite sve višekratnike za svaku poziciju.
• Odaberite najmanje zajedničkog više.

Drugi način:

• Rasporedite sve brojeve u osnovne čimbenike.
• U redak upišite sve pregrade prvog broja i dodajte ovdje one čimbenike koji su u drugim proširenjima, ali nedostaju u prvom.
• Izračunajte proizvod.

GCD u Pascalu: algoritam rada

Kako pronaći gcd od dva broja? "Pascal" je programski jezik u kojem će se kod pisati. Prvo morate slijediti gore navedeni algoritam. I ovdje dolazi do spašavanja matematike. Algoritam zadatka pomoći će pronaći GCD dva prirodna broja. U Turbo Pascalu će izgledati ovako:

• Prikažite upit za unos 2 ne-negativnih brojeva s tipkovnice.
• Pokrenite while petlju, gdje je uvjet broj 1 <> broj 2 (uvjetno, a i b).
• Tijelo ciklusa obuhvaća sljedeće radnje: ako je a> b, onda a: = a - b, inače b: = b - a.
• Prikaz rezultata.

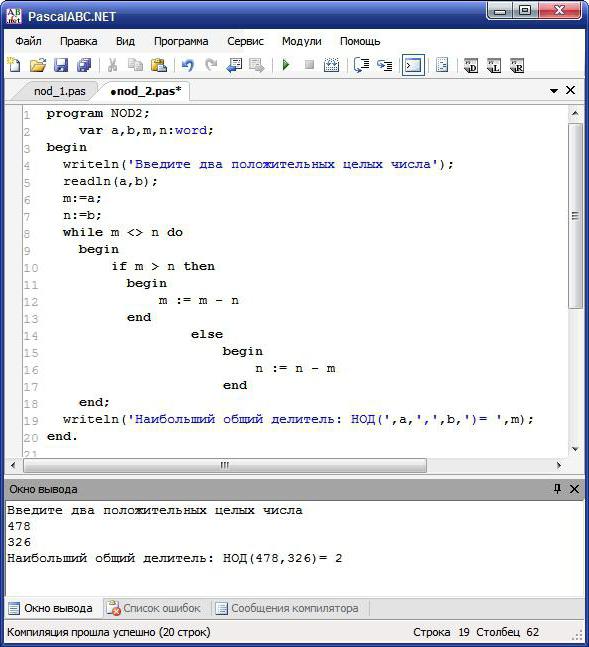
NOD u Pascalu: euklidsko rješenje

Kako pronaći GCD dva broja jednostavnom, ali učinkovitom metodom?

• Unos pozitivnih brojeva.
• Poziv pisanoj funkciji koja izračunava gcd. Sama funkcija obavlja sljedeće radnje: provjeru stanja, koji je veći broj; dodjeljivanje početnih podataka drugim varijablama; u ciklusu s preduvjetom (r2 <> 0, tj. sve dok varijabla nije jednaka 0), nađen je ostatak dijeljenja i rezultati su dodijeljeni varijablama; dodjeljivanje imena funkcije završenog rezultata.
• Prikaz rezultata na zaslonu.

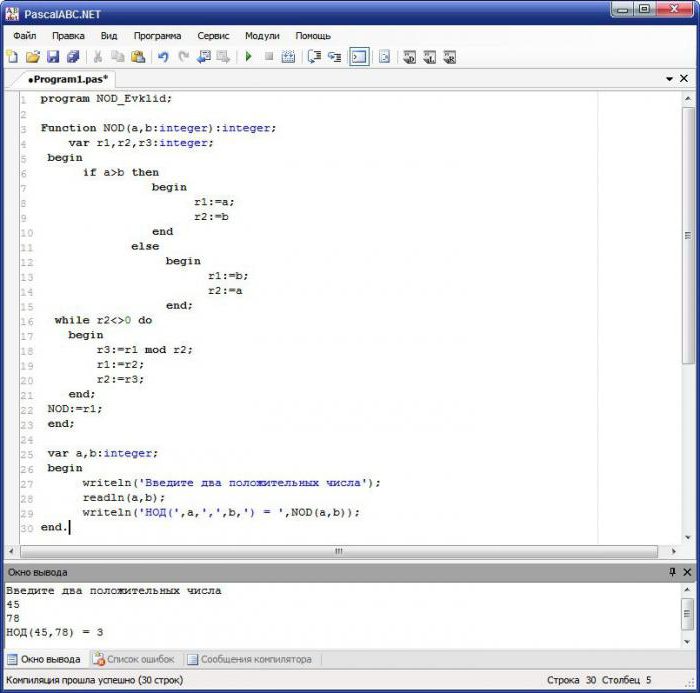
Mnogi programeri vjeruju da su obje mogućnosti za pronalaženje GCD-a vrlo slične, tako da se na Internetu prva metoda može dati kao euklidski algoritam.

NOC u Pascalu: kako je program uređen?

Već su razmotrena 2 algoritma koji objašnjavaju kako pronaći GCD dva broja. Sada ostaje da saznate kako program za pretraživanje NOC-a gleda u Turbo Pascalu. Algoritam rada pri programiranju je sljedeći:

• Unesite dva broja.
• Dodjeljivanje dvije druge varijable danim vrijednostima.
• Pronalaženje proizvoda izvornih elemenata.
• U petlji s preduvjetom (dok), uredite uvjet: ako je prvi broj veći od drugog (n> m), rezultat (n: = n - m) možete pronaći oduzimanjem; inače izvršite ovu operaciju, ali u suprotnom smjeru (m: = m - n).
• Prikažite rezultat u kojem će pronađeni proizvod biti podijeljen funkcijom div brojem m.

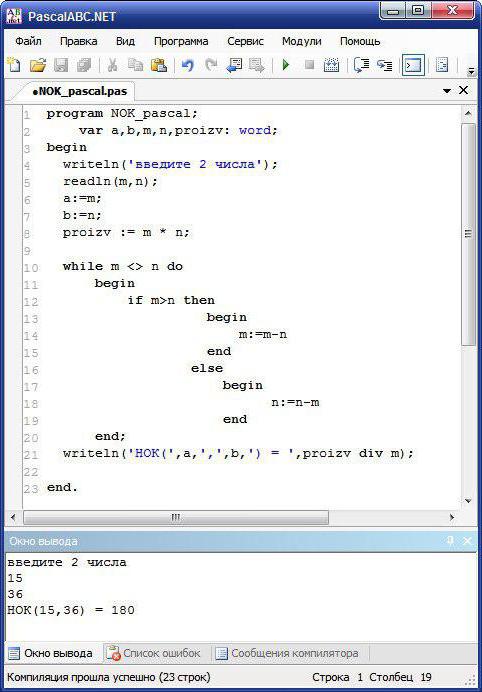
Za koje su dvije varijable a i b uvedene? Da biste ispravno prikazali rezultat. U ciklusu s preduvjetom, izvorne vrijednosti varijabli se gube, tako da je nemoguće iznijeti m, n vrijednosti koje je odredio korisnik u zagradama. Naravno, redak 21 može se uvelike pojednostaviti pisanjem samo pisanja (proizv div m). No, korisnik, koji će najprije biti upoznat s programom, neće razumjeti što se prikazuje na zaslonu.

Ručno praćenje:

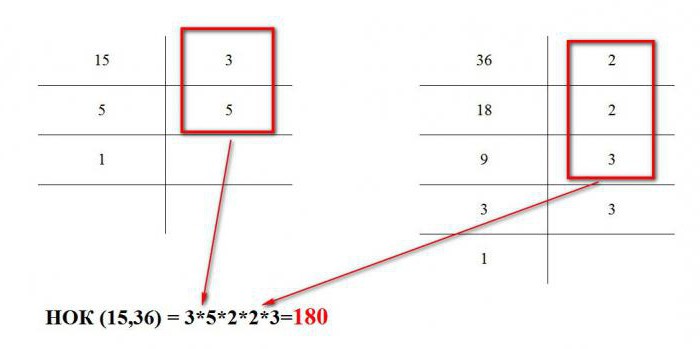
Kao što možete vidjeti, ne postoji ništa teško naći rješenje za GCD i NOO: ni u Pascalu, niti, zapravo, u matematici.