Kako pronaći radijus kruga. Upisana i ograničena kružnica

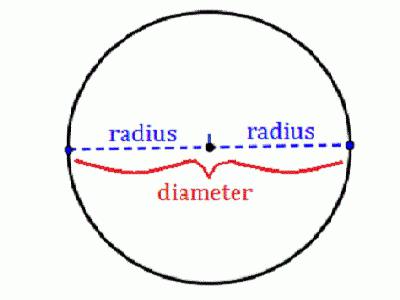
Polumjer je segment koji povezuje bilo koju točku na krugu sa središtem. To je jedna od najvažnijih karakteristika ove brojke, jer na temelju nje možete izračunati sve ostale parametre. Ako znate kako pronaći radijus kruga, tada možete izračunati njegov promjer, duljinu i područje. U slučaju da je ova figura upisana ili opisana oko druge, tada se može riješiti niz zadataka. Danas ćemo ispitati osnovne formule i značajke njihove primjene.

Poznate vrijednosti

Ako znate kako pronaći radijus kruga, koji je obično označen slovom R, on se može izračunati iz jedne karakteristike. Ove vrijednosti uključuju:

• opseg (C);
• promjer (D) je segment (ili bolje rečeno akord) koji prolazi kroz središnju točku;
• područje (S) - prostor, koji je ograničen na tu brojku.

Duž oboda

Ako je vrijednost C poznata u zadatku, tada je R = C / (2 * P). Ova formula je derivat. Ako znamo što je to duljina opsega onda se ne mora sjetiti. Pretpostavimo da u zadatku C = 20 m. Kako pronaći radijus kruga u ovom slučaju? Jednostavno zamijenite poznatu vrijednost u gornjoj formuli. Napominjemo da se u takvim problemima uvijek podrazumijeva poznavanje broja P. Za praktičnost izračuna uzimamo njegovu vrijednost kao 3.14. Rješenje u ovom slučaju je sljedeće: zapišite koje su vrijednosti dane, izvedite formulu i izvršite izračune. U odgovoru pišemo da je radijus 20 / (2 * 3,14) = 3,19 m. Važno je ne zaboraviti ono što smo mislili i spomenuti ime mjernih jedinica.

Po promjeru

Odmah ističemo da je to najjednostavniji tip problema koji pita kako pronaći radijus kruga. Ako dobijete takav primjer na kontroli, onda možete biti mirni. Ne treba čak ni kalkulator! Kao što smo rekli, promjer je segment ili, točnije, akord koji prolazi kroz centar. Štoviše, sve točke kruga su jednako udaljene. Stoga se ovaj akord sastoji od dvije polovice. Svaki od njih je radijus, koji slijedi iz njegove definicije kao segmenta koji povezuje točku na krugu i njegovo središte. Ako je poznati promjer problema, tada za pronalaženje radijusa trebate samo podijeliti tu vrijednost na dva. Formula je sljedeća: R = D / 2. Na primjer, ako je promjer u problemu 10 m, onda je radijus 5 metara.

Po području kruga

Ova vrsta zadatka se obično naziva najteže. To je prvenstveno zbog nepoznavanja formule. Ako znate kako pronaći radijus kruga u ovom slučaju, onda je ostalo pitanje tehnike. U kalkulatoru morate samo unaprijed pronaći ikonu kvadratnog korijena. Područje kruga je proizvod broja P, a radijus pomnožen sam po sebi. Formula je sljedeća: S = P * R2. Razdvajanjem radijusa na jednoj strani jednadžbe, lako možete riješiti problem. Bit će jednako kvadratni korijen iz kvocijenta područja podijeljeno brojem P. Ako je S = 10 m, tada je R = 1,78 metara. Kao iu prethodnim zadacima, važno je ne zaboraviti na korištene jedinice.

Kako pronaći polumjer kružnice

Pretpostavimo da su a, b, c strane trokuta. Ako znate njihove vrijednosti, možete pronaći radijus kruga opisan oko njega. Da biste to učinili, najprije morate pronaći polu-perimetar trokuta. Da bismo vam olakšali čitanje, označimo ga malim slovom str. To će biti jednako polovici iznosa stranaka. Njegova formula je: p = (a + b + c) / 2.

Također izračunajte proizvod dužine stranica. Radi praktičnosti, označavamo ga slovom S. Formula za radijus opisne kružnice će izgledati ovako: R = S / (4 * √ (p * (p -)) (p - b) * (p - c)).

Razmotrite jedan primjer zadatka. Imamo krug opisan oko trokuta. Duljine njegovih stranica iznose 5, 6 i 7 cm. Prvo izračunamo poluprečnik. U našem problemu bit će jednak 9 centimetara. Sada izračunamo produkt duljina stranica - 210. Rezultate međukalkulacija zamjenjujemo formulom i nađemo rezultat. Radijus opisane kružnice je 3,57 centimetara. Zapisujemo odgovor, ne zaboravljajući na mjerne jedinice.

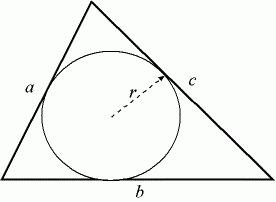
Kako pronaći radijus upisane kružnice

Pretpostavimo da su a, b, c duljine stranica trokuta. Ako poznajete njihove vrijednosti, tada možete pronaći radijus kružnice u njemu. Prvo morate pronaći njegov polu-perimetar. Radi lakšeg razumijevanja, označavamo ga malim slovom str. Formula za izračunavanje je sljedeća: p = (a + b + c) / 2. Ova vrsta zadatka je nešto jednostavnija od prethodne, pa više nisu potrebni nikakvi prijelazni proračuni.

Polumjer upisane kružnice izračunava se slijedećom formulom: R = √ ((p - a) * (p - b) * (p - c) / p). Razmotrite ovo sa specifičnim primjerom. Pretpostavimo da problem opisuje trokut sa stranicama od 5, 7 i 10 cm, u koji je upisana kružnica čiji se radijus nalazi. Prvo nalazimo polu-perimetar. U našem problemu bit će jednak 11 cm, a sada ga zamjenjujemo glavnom formulom. Radijus će biti jednak 1.65 centimetara. Zapisujemo odgovor i ne zaboravljamo ispravne jedinice.

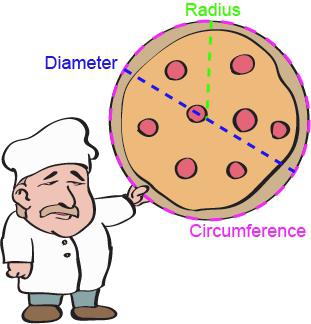
Krug i njegova svojstva

svaki geometrijski oblik ima svoje osobine. Iz njihova shvaćanja ovisi ispravnost rješavanja problema. Imaju krug. Često se koriste u rješavanju primjera s likovima opisanim ili upisanim, jer daju jasnu predodžbu o toj situaciji. Među njima su:

• Ravna crta može imati nulu, jednu ili dvije točke presjeka s krugom. U prvom slučaju se s njom ne siječe, u drugom je tangenta, u trećem - sekant.
• Ako uzmemo tri točke koje ne leže na jednoj pravoj liniji, onda se kroz njih može nacrtati samo jedan krug.
• Ravna crta može biti tangenta od dvije figure odjednom. U tom slučaju, proći će kroz točku koja leži na segmentu koji povezuje središta krugova. Njegova duljina jednaka je zbroju radijusa tih figura.
• Kroz jednu ili dvije točke možete nacrtati beskonačan broj krugova.