Molekularna težina: osnovna načela definicije

Molekularna masa je jedan od temeljnih pojmova u suvremenoj kemiji. Njegovo uvođenje omogućeno je nakon znanstvene utemeljenosti Avogadrove tvrdnje da se mnoge tvari sastoje od sitnih čestica - molekula, od kojih se svaka sastoji od atoma. Znanost duguje ovu presudu talijanskom kemičaru Amadeo Avogadro, koji je znanstveno potkrijepljen molekularna struktura tvari i kemija dali su mnoge važne pojmove i zakone.

Jedinice mase elemenata

U početku je atom vodika uzet kao najlakši element u svemiru kao osnovna jedinica atomske i molekularne težine. No, većina atomskih masa izračunata je na temelju njihovih kisikovih spojeva, pa je odlučeno odabrati novi standard za određivanje atomskih masa. Pretpostavljalo se da je atomska masa kisika 15, atomska masa najsvjetlije tvari na Zemlji, vodik, 1. Godine 1961. kisikov sustav za određivanje težine bio je čest, ali je stvorio određene neugodnosti.

Godine 1961. usvojena je nova skala. relativne atomske mase Referenca za koju je bio izotop ugljika ¹² C. Jedinica atomske mase (skraćeno Amu) je 1/12 mase ovog standarda. Trenutno, atomska masa je masa atoma, koja bi trebala biti izražena u amu.

Masa molekula

Masa molekule bilo koje tvari jednaka je zbroju masa svih atoma koji tvore danu molekulu. Najmanja molekularna težina plina je u vodiku, njegov spoj je napisan kao H2 i ima vrijednost blizu dva. Molekula vode sastoji se od atoma kisika i dva atoma vodika. To znači da je njegova molekularna težina 15,994 ± 2 x 1,0079 = 18,0152 amu. Najveće molekularne mase imaju složene organske spojeve - proteine ​​i aminokiseline. Molekulska masa strukturne jedinice proteina kreće se od 600 do 10 ⁶ i više, ovisno o broju peptidnih lanaca u ovoj makromolekularnoj strukturi.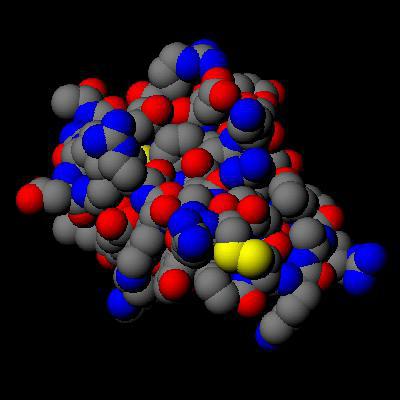

krtica

Istodobno sa standardnim jedinicama mase i volumena, u kemiji se koristi vrlo posebna jedinica sustava, krtica.

Krtica je količina tvari koja sadrži onoliko strukturnih jedinica (iona, atoma, molekula, elektrona), koliko je sadržano u 12 grama izotopa ¹² C.

Prilikom primjene mjere količine tvari potrebno je naznačiti koje su strukturne jedinice. Kao što proizlazi iz pojma "krtica", u svakom pojedinačnom slučaju treba točno odrediti na koje se strukturne jedinice odnosi - na primjer, mol H ⁺ iona, mol H ₂ molekula i tako dalje.

Molarna i molekularna težina

Masa tvari u 1 molu mjeri se u g / mol i naziva se molarna masa. Odnos molekulske i molarne mase može se napisati kao jednadžba.

ν = k × m / M, gdje je k koeficijent proporcionalnosti.

Lako je reći da će za svaki omjer koeficijent proporcionalnosti biti jednak jednom. Zaista, izotop ugljika ima relativnu molekularnu masu od 12 AU.m, i, po definiciji, molarna masa ove tvari je 12 g / mol. Odnos molekulske mase prema molarnoj razini je 1. Prema tome možemo zaključiti da molarna i molekularna težina imaju iste numeričke vrijednosti.

Količina plina

Kao što znate, sve tvari oko nas mogu biti u čvrstom, tekućem ili plinovitom agregatnom stanju. Za krute tvari najčešća osnovna mjera je masa, za krute tvari i tekućine, volumen. To je zbog činjenice da krute tvari zadržavaju oblik i konačne dimenzije, a tekuće i plinovite tvari nemaju konačne dimenzije. Značajka bilo kojeg plina je da je udaljenost između njegovih strukturnih jedinica - molekula, atoma, iona - mnogo puta veća od istih udaljenosti u tekućinama ili krutim tvarima. Na primjer, jedan mol vode u normalnim uvjetima zauzima volumen od 18 ml - približno jednake veličine uklapa se u jednu žlicu. Volumen jednog mola fine kristalne soli je 58,5 ml, a volumen 1 mola šećera je 20 puta više mola vode. Potrebno je više prostora za plinove. Jedan mol dušika u normalnim uvjetima zauzima volumen od 1.240 puta više od jednog mola vode.

Tako se količine plinovitih tvari značajno razlikuju od volumena tekućine i krute tvari. To je zbog razlike u udaljenostima između molekula tvari u različitim agregacijskim stanjima.

Normalni uvjeti

Stanje bilo kojeg plina u velikoj mjeri ovisi o temperaturi i tlaku. Na primjer, dušik na temperaturi od 20 ° C zauzima volumen od 24 litre, a na 100 ° C pri istom tlaku - 30,6 litara. Kemičari su uzeli u obzir tu ovisnost, pa je odlučeno sve operacije i mjerenja s plinovitim tvarima svesti na normalne uvjete. Širom svijeta, parametri normalnih uvjeta su isti. Za plinovite kemikalije to su:

• Temperatura na 0 ° C.
• Tlak 101,3 kPa.

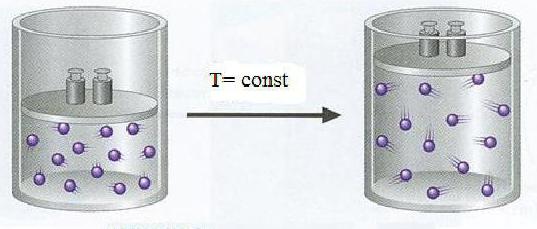
Za normalne uvjete prihvaća se posebna kratica - n. Ponekad ova oznaka nije napisana u zadacima, onda biste trebali pažljivo ponovno pročitati uvjete problema i dovesti parametre plina u normalne uvjete.

Izračunajte volumen 1 mola plina

Kao primjer, lako je izračunati jedan mol bilo kojeg plina, na primjer dušika. Da biste to učinili, najprije morate pronaći vrijednost njegove relativne molekularne težine:

_Mr (N2) = 2 × 14 = 28.

Kako je relativna molekulska masa tvari brojčano jednaka molarnoj, tada M (N2) = 28 g / mol.

Pokusno je utvrđeno da u normalnim uvjetima gustoća dušika iznosi 1,25 g / l.

Ovu vrijednost zamjenjujemo standardnom formulom poznatom iz školskog tečaja fizike, gdje:

• V je volumen plina;
• m je masa plina;
• ρ je gustoća plina.

Dobiva se molarni volumen dušika u normalnim uvjetima

V (N2) = 25 g / mol: 1,25 g / litra = 22,4 1 / mol.

Ispada da jedan mol dušika traje 22,4 litre.

Ako takvu operaciju izvodite sa svim postojećim plinovitim tvarima, možete doći do iznenađujućeg zaključka: volumen bilo kojeg plina u normalnim uvjetima je 22,4 litara. Bez obzira na to koji je plin uključen, kakva je njegova struktura i fizikalno-kemijske karakteristike, jedan mol tog plina će zauzeti volumen od 22,4 litre.

Molarni volumen plina je jedna od najvažnijih konstanti u kemiji. Ova konstanta omogućuje rješavanje mnogih kemijskih problema povezanih s mjerenjem svojstava plinova u normalnim uvjetima.

rezultati

Molekulska masa plinovitih tvari važna je za određivanje količine tvari. A ako istraživač zna količinu tvari iz plina, može odrediti masu ili volumen takvog plina. Za isti dio plinovite tvari istovremeno su ispunjeni uvjeti:

ν = m / M ν = V / V _m.

Ako uklonimo konstantu ν, možemo izjednačiti ova dva izraza:

m / M = V / V _m.

Tako možete izračunati masu jednog dijela tvari i njezin volumen, a također postaje poznata molekularna težina ispitivane tvari. Koristeći ovu formulu, lako se može izračunati omjer volumen-masa. Kod izlijevanja ove formule u oblik M = m V _m / V, poznata je molarna masa željenog spoja. Da bi se izračunala ta vrijednost, dovoljno je znati masu i volumen ispitnog plina.

Treba imati na umu da je stroga podudarnost stvarne molekularne mase tvari s onom koju je pronašla formula nemoguća. Svaki plin sadrži masu nečistoća i aditiva koji mijenjaju njegovu strukturu i utječu na određivanje njegove mase. Ali te fluktuacije mijenjaju treću ili četvrtu znamenku nakon decimalne točke u pronađenom rezultatu. Stoga su za školske probleme i eksperimente pronađeni rezultati prilično uvjerljivi.