Kretanje nabijene čestice u magnetskom polju: formule. Kretanje nabijenih čestica u jednoličnom magnetskom polju

Kao što je poznato, električno polje se obično karakterizira veličinom sile s kojom djeluje na probnu jedinicu električni naboj Magnetsko polje tradicionalno karakterizira sila kojom djeluje na vodič s "jednom" strujom. Međutim, kako teče, uređeno kretanje nabijenih čestica događa se u magnetskom polju. Stoga možemo odrediti magnetsko polje B u nekom trenutku u prostoru s gledišta magnetske sile F _B koju polje vrši na česticu dok se kreće u njoj s brzinom v.

Opća svojstva magnetske sile

Eksperimenti u kojima je promatrano kretanje nabijenih čestica u magnetskom polju daju sljedeće rezultate:

• Magnituda F _B magnetske sile koja djeluje na česticu proporcionalna je naboju q i brzini v čestice.
• Ako se gibanje nabijene čestice u magnetskom polju odvija paralelno s vektorom ovog polja, tada sila koja djeluje na nju je nula.
• Kada vektor brzine čestica napravi bilo koji kut θ 0 s magnetskim poljem, tada sila djeluje u smjeru okomitom na v i B; to jest, F _{B je} okomito na ravninu koju čine v i B (vidi sliku ispod).
• Magnituda i smjer F _B ovise o brzini čestica i o veličini i smjeru magnetskog polja B.
• Smjer sile koja djeluje na pozitivni naboj suprotan je smjeru iste sile koja djeluje na negativni naboj koji se kreće u istom smjeru.
• Magnetna sila koja djeluje na pokretnu česticu proporcionalna je grijehu θ kuta θ između vektora v i B.

Lorenzova sila

Gornja opažanja možemo sažeti bilježenjem magnetske sile kao F _B = x x B.

Kada se nabijena čestica kreće u magnetskom polju, Lorentzova sila F _B s pozitivnim q usmjerena je duž vektorskog proizvoda vx B. To je, po definiciji, okomito na oba v i B. Ovu jednadžbu smatramo radnom definicijom magnetskog polja u nekom trenutku u prostoru. To jest, definira se u smislu sile koja djeluje na česticu dok se kreće. Stoga se gibanje nabijene čestice u magnetskom polju može kratko definirati kao kretanje pod djelovanjem te sile.

Na naboj koji se kreće brzinom v u prisutnosti i električnog polja E i magnetskog B utječe i električna sila qE i magnetski qv x B. Ukupni učinak koji se primjenjuje na njega je F _L = qE + qv x B. tako: punom snagom Lorentza.

Kretanje nabijenih čestica u jednoličnom magnetskom polju

Razmotrimo sada poseban slučaj pozitivno nabijene čestice koja se kreće u jednoličnom polju, s početnim vektorom brzine okomito na nju. Pretpostavimo da je vektor B polja usmjeren po stranici. Slika ispod pokazuje da se čestica kreće u krugu u ravnini okomitoj na B.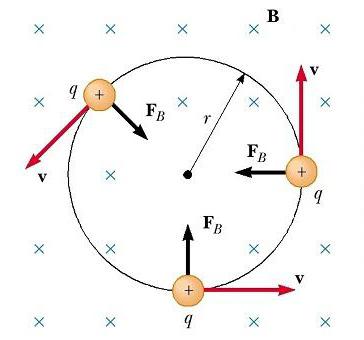

Kružno gibanje nabijene čestice u magnetskom polju događa se jer je magnetska sila F _B usmjerena pod pravim kutom na v i B i ima konstantnu vrijednost qvB. Kako sila skreće čestice, smjerovi v i F _{B se} stalno mijenjaju, kao što je prikazano na slici. Budući da je F _B uvijek usmjeren prema središtu kruga, on samo mijenja smjer v, a ne njegovu vrijednost. Kao što je prikazano na slici, kretanje pozitivno nabijene čestice u magnetskom polju događa se suprotno od smjera kazaljke na satu. Ako je q negativno, rotacija će se pojaviti u smjeru kazaljke na satu.

Dinamika kružnog gibanja čestice

Koji parametri karakteriziraju gore opisano gibanje nabijene čestice u magnetskom polju? Formule za njihovo određivanje možemo dobiti, ako uzmemo prethodnu jednadžbu i izjednačimo F _B centrifugalnu silu potrebnu za održavanje kružne putanje gibanja: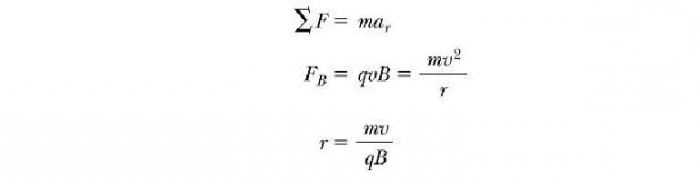

To jest, radijus kruga je proporcionalan momentu mv čestice i obrnuto proporcionalan veličini njegova naboja i magnetskog polja. Kutna brzina čestica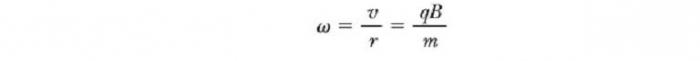

Razdoblje s kojim se naelektrizirana čestica kreće u magnetskom polju u krugu je jednako obod, podijeljeno svojom linearnom brzinom: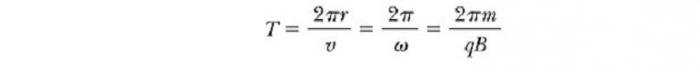

Ovi rezultati pokazuju da kutna brzina čestice i vrijeme kružnog gibanja ne ovise o linearnoj brzini ili o radijusu orbite. Kutna brzina ω se često naziva ciklotron. frekvencija (kružna), jer nabijene čestice kruže s njom u akceleratorskom tipu koji se naziva ciklotron.

Kretanje čestice pod kutom prema vektoru magnetskog polja

Ako vektor brzine brzine čestica v oblikuje neki proizvoljni kut u odnosu na vektor B, njegova je putanja heliks. Primjerice, ako je jednoliko polje usmjereno duž osi x, kao što je prikazano na slici ispod, tada nema komponente magnetske sile F _B u tom smjeru. Kao rezultat, komponenta ubrzanja je _x = 0, a x-komponenta brzine čestice je konstantna. Međutim, magnetska sila F _B = qv x B uzrokuje vremensku varijaciju komponenti brzine v _y i v _z . Kao rezultat, nabijena čestica se kreće u magnetskom polju duž spirale čija je os paralelna magnetskom polju. Projekcija putanje na yz ravninu (kada se gleda duž x osi) je krug. Njegove projekcije na xy i xz ravni su sinusoidi! Jednadžbe gibanja ostaju iste kao na kružnoj putanji, pod uvjetom da je v zamijenjen s ν _⊥ = √ (ν _u ² + ν _z ² ).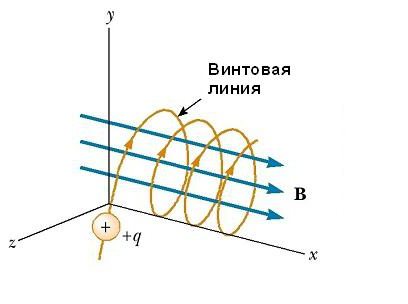

Nehomogeno magnetsko polje: kako se u njemu kreću čestice

Kretanje nabijene čestice u magnetskom polju, koje je nehomogeno, događa se duž složenih trajektorija. Dakle, u polju čija se veličina povećava na rubovima svog područja postojanja i oslabljuje u svojoj sredini, kao što je, na primjer, prikazano na slici ispod, čestica može oscilirati naprijed-natrag između krajnjih točaka. 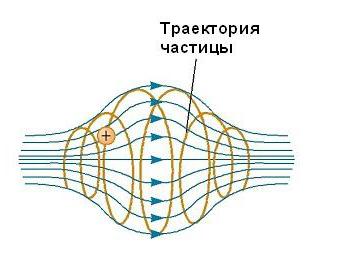Napunjena čestica počinje na jednom kraju spirale, rane se po silama i kreće se uz nju sve dok ne dosegne drugi kraj, gdje se vraća natrag. Ova konfiguracija je poznata kao "magnetska boca", jer nabijene čestice mogu biti zarobljene u njoj. Koristio se za ograničavanje plazme, plina koji se sastoji od iona i elektrona. Takva shema zatvaranja plazme može odigrati ključnu ulogu u kontroli nuklearne fuzije, procesa koji nam daje gotovo beskonačan izvor energije. Nažalost, "magnetska boca" ima svoje probleme. Ako je veliki broj čestica zarobljen, sudari između njih uzrokuju njihovo curenje iz sustava.

Kako Zemlja utječe na kretanje kozmičkih čestica

Van Allenovi zemljani pojasevi u blizini Zemlje sastoje se od nabijenih čestica (uglavnom elektrona i protona) koje okružuju Zemlju u obliku toroidnih područja (vidi donju sliku). Kretanje nabijene čestice u magnetskom polju Zemlje odvija se spiralom oko linija sile od pola do pola, prekrivajući tu udaljenost za nekoliko sekundi. Te čestice dolaze uglavnom od Sunca, ali neke dolaze iz zvijezda i drugih nebeskih objekata. Zbog toga se nazivaju kozmičkim zrake. Većina njih odstupa Zemljino magnetsko polje i nikada ne dostiže atmosferu. Međutim, neke od čestica padaju u zamku, one čine Van Allenov pojas. Kad su iznad polova, ponekad se sudaraju s atomima u atmosferi, zbog čega emitiraju vidljivo svjetlo. Dakle, u sjevernoj i južnoj hemisferi postoje prekrasne aurore. Oni se obično javljaju u polarnim regijama, jer se ovdje Van Allenovi pojasevi nalaze najbliže površini Zemlje.

Ponekad, međutim, Sunčeva aktivnost uzrokuje da veći broj nabijenih čestica ulazi u ove pojaseve i značajno narušava normalnu silu magnetskog polja povezanog sa Zemljom. U takvim situacijama, aurora se ponekad može vidjeti na nižim geografskim širinama.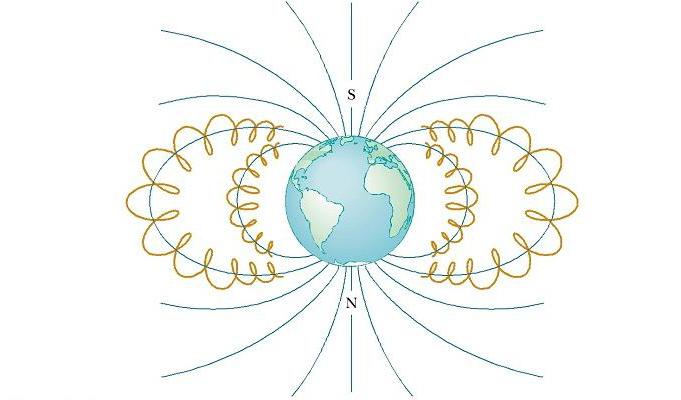

Izbornik brzine

U mnogim eksperimentima u kojima se kretanje nabijenih čestica događa u jednoličnom magnetskom polju, važno je da se sve čestice kreću gotovo istom brzinom. To se može postići primjenom kombinacije električnog polja i magnetskog polja, orijentiranog kao što je prikazano na donjoj slici. Homogeno električno polje usmjereno je okomito prema dolje (u ravnini stranice), a isto magnetno polje se primjenjuje u smjeru okomitom na električni (po stranici). 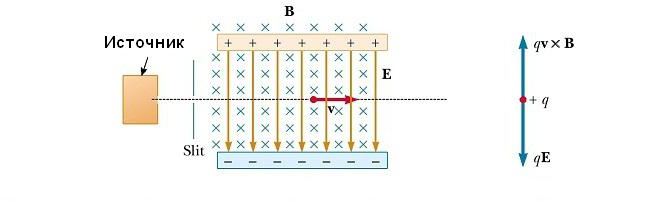Za pozitivni q, magnetska sila F _B = qv x B usmjerena je prema gore, a električna sila qE je spuštena. Kada su vrijednosti dvaju polja odabrane tako da je qE = qvB, čestica se kreće u ravnoj horizontalnoj liniji kroz područje polja. Iz izraza qE = qvB nalazimo da samo čestice s brzinom v = E / B prolaze bez odstupanja kroz međusobno okomito električno i magnetsko polje. Sila F _{B koja} djeluje na čestice koje se kreću brzinom većom od v = E / B ispada da je više električna, te se odbijaju prema gore. Oni koji se kreću nižom brzinom odstupaju prema dolje.

Maseni spektrometar

Ovaj uređaj razdvaja ione u skladu s omjerom njihove mase za punjenje. Prema jednoj verziji ovog uređaja, poznatoj kao Bainbridge maseni spektrometar, ionski snop najprije prolazi kroz selektor brzine, a zatim ulazi u drugo polje B0, koje je također homogeno i ima isti smjer kao polje u selektoru (vidi sliku ispod) , Nakon što uđe u njega, gibanje nabijene čestice u magnetskom polju u polukrugu radijusa r prije udara u fotografsku ploču R. Ako su ioni pozitivno nabijeni, snop se skreće prema gore, kao što je prikazano na slici. Ako su ioni negativno nabijeni, snop će se odbiti prema dolje. Iz izraza za radijus kružne putanje čestice možemo pronaći omjer m / q

i onda, koristeći jednadžbu v = E / B, nalazimo to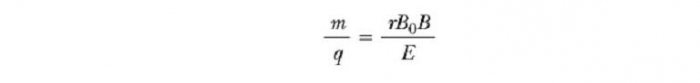

Tako m / q možemo odrediti mjerenjem radijusa zakrivljenosti, znajući polja B, B i E. U praksi, to obično mjeri mase raznih izotopa danog iona, budući da svi nose jednu naboj q. Stoga se omjer mase može odrediti čak i ako je q nepoznat. Varijaciju ove metode upotrijebio je J.J. Thomson (1856-1940) 1897. godine za mjerenje omjera e / m _e za elektrone.

ciklotron

Može ubrzati nabijene čestice do vrlo velikih brzina. I električne i magnetske sile ovdje igraju ključnu ulogu. Dobivene čestice visoke energije koriste se za bombardiranje atomskih jezgri, a time i za proizvodnju nuklearnih reakcija od interesa za istraživače. Brojne bolnice koriste ciklotronsku opremu za proizvodnju radioaktivnih tvari za dijagnozu i liječenje.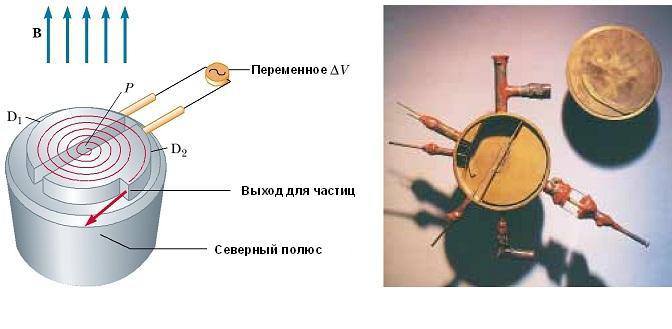

Shematski prikaz ciklotrona prikazan je na Sl. u nastavku. Čestice se kreću unutar dva polu-cilindrična spremnika D1 i D2, nazvana deants. Visokofrekventna varijabilna potencijalna razlika primjenjuje se na deeze odvojene razmakom, a jednolično magnetsko polje je usmjereno uzduž osi ciklotrona (južni pol njegovog izvora nije prikazan na slici).

Pozitivni ion otpušten iz izvora u točki P u blizini središta uređaja u prvom dualu kreće se duž polukružne putanje (prikazane crvenom crtom na slici) i vraća se u prorez u trenutku T / 2, gdje je T vrijeme jedne potpune revolucije unutar dva duanta. ,

Učestalost primijenjene razlike potencijala regulirana je na takav način da su polarnosti diantesa obrnute u trenutku kada ion izlazi iz jednog diantha. Ako se primijenjena razlika potencijala prilagodi tako da u ovom trenutku D2 dobije qΔV niži električni potencijal od D ₁ , ion se ubrzava u praznini prije ulaska u D ₂ , a njegova kinetička energija se povećava za qΔV. Zatim se kreće oko D ₂ duž polukružne putanje većeg radijusa (jer je njegova brzina povećana).

Nakon nekog vremena T / 2, on ponovno ulazi u jaz između deantsa. U ovom trenutku, polariteti duentsa se ponovno mijenjaju, a jonu prolazi još jedan "udarac" kroz prazninu. Kretanje nabijene čestice u magnetskom polju u spirali nastavlja se, tako da sa svakim prolazom jednog duanta ion dobiva dodatnu kinetičku energiju jednaku qΔV. Kada se polumjer njegove putanje približi radijusu deea, ion napušta sustav kroz izlazni prorez. Važno je napomenuti da se rad ciklotrona temelji na činjenici da T ne ovisi o brzini iona i radijusu kružne putanje. Možemo dobiti izraz za kinetička energija kada napusti ciklotron, ovisno o radijusu R dees. Znamo da je brzina kružnog gibanja čestice ν = qBR / m. Dakle, njegova kinetička energija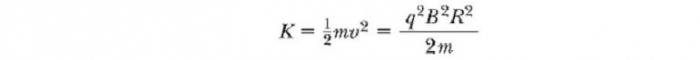

Kada energija iona u ciklotronu prelazi oko 20 MeV, dolazi do relativističkih učinaka. Napominjemo da se T povećava i da pokretni ioni ne ostaju u fazi s primijenjenom potencijalnom razlikom. Neki akceleratori rješavaju taj problem promjenom razdoblja primijenjene razlike potencijala, tako da ostaju u fazi s pokretnim ionima.

Učinak Halla

Kada se vodič u struji postavi u magnetsko polje, stvara se dodatna razlika potencijala u smjeru okomitom na smjer struje i magnetskog polja. Ovaj fenomen, kojeg je Edwin Hall (1855-1938) prvi put uočio 1879., poznat je kao Hall. Uvijek se promatra kada se nabijena čestica kreće u magnetskom polju. To dovodi do otklona nositelja na jednoj strani vodiča kao posljedice magnetske sile koju doživljavaju. Hallov efekt daje informacije o znaku nositelja naboja i njihovoj gustoći, a može se koristiti i za mjerenje veličine magnetskih polja.

Uređaj za promatranje Hall efekta sastoji se od ravnog vodiča s strujom I u smjeru x, kao što je prikazano na donjoj slici. 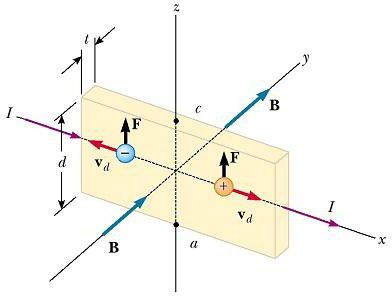Homogeno polje B primjenjuje se u y smjeru. Ako su nositelji naboja elektroni koji se kreću duž x osi s brzinom pomicanja v _d , tada doživljavaju usmjerenu prema gore (uzimajući u obzir negativnu q) magnetsku silu F _B = qvdxB, skreću se prema gore i akumuliraju na gornjem rubu ravnog vodiča, što rezultira višak pozitivnog naboja pojavljuje se na donjem rubu. Ova akumulacija naboja na rubovima se povećava sve dok električna sila koja proizlazi iz razdvajanja naboja ne uravnoteži magnetsku silu koja djeluje na nosače. Kada se dostigne ta ravnoteža, elektroni se više ne skreću prema gore. Osjetljivi voltmetar ili potenciometar povezan s gornjim i donjim rubovima vodiča može izmjeriti razliku potencijala poznatu kao Hall napon.