Pregled različitih vrsta prizmi. Svojstva trokutastih prizmi

Prizma je jedna od poznatih figura u prostoru, čija se svojstva detaljno proučavaju u školskom smjeru geometrije. Ovaj je članak pregled različitih vrsta prizmi i njihovih karakteristika. Karakteristike trokutaste prizme detaljnije su opisane.

Što je prizma?

Članak započinje s definicijom prizme u geometriji. Ispod toga, figura bi trebala biti formirana od dvije identične paralelne strane, koje su ravne n-gons, i n strana paralelograma. Bilo koji oblik koji zadovoljava snimljenu definiciju bit će prizma.

Graditi prizmu pomoću geometrijskih operacija nije teško. Potrebno je samo uzeti apsolutno bilo koji n-gon i prebaciti ga paralelno sebi za određeni segment u prostoru.

Budući da se radi o poliedru (koji se sastoji od poligonalnih lica), ne može se geometrijski dobiti rotacijom, kao što je to moguće za cilindar ili konus.

Svaka prizma ima dvije osnove, koje su predstavljene jednakim n-gonima i n paralelograma (ponekad mogu biti pravokutnici, kvadrati ili rombovi), čija ukupnost čini bočnu površinu figure. Također, lik je karakteriziran s 2 * n jednakim vrhovima i 3 * n rubovima, gdje je n broj strana (vrhova) poligonalne baze.

Kako su prizme klasificirane?

Broj različitih prizmi je beskonačan. Svi se međusobno razlikuju po obliku i linearnim dimenzijama, međutim, postoje samo dvije značajke njihove geometrijske strukture, koje su temelj moderne klasifikacije dotične klase figura. Ove su značajke sljedeće:

• osnovni poligon;
• kutovi između stranica i baza.

Na izgled prizme ne utječu nikakvi drugi parametri od gore navedenih. Obje značajke zajedno dovode do podjele cijelog razreda na četiri tipa ili tipova figura:

• konveksni i konkavni;
• trokutasti četverokutni, ..., n-ugljik;
• ravna i nagnuta;
• dobro i krivo.

Razmotrimo detaljnije svaku od ovih vrsta prizmi čija su svojstva jedinstveno određena gornjom klasifikacijom.

Konveksne i konkavne figure

Mnogi ljudi zaboravljaju ovu klasifikacijsku točku kada karakteriziraju prizme, jer u svim geometrijskim problemima, u pravilu, pojavljuju se istaknute figure. Tako se naziva konveksna prizma, koja na bazi ima konveksni poligon. Prema tome, ako je poligon konkavan, prizma će također biti konkavna.

U nastavku će se prikazati samo konveksne prizme, ali ovdje ćemo pokazati, na primjer, kako izgleda konkavna prizma u obliku zvijezde.

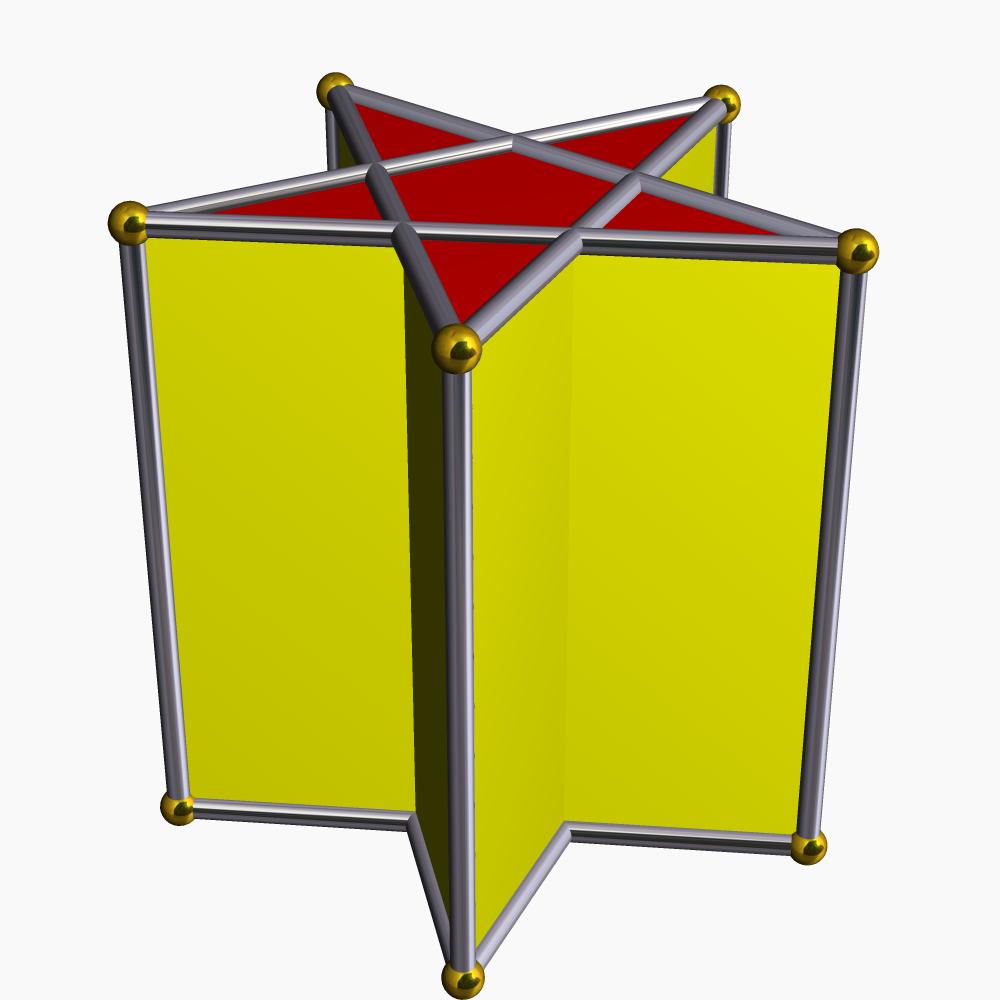
Treba primijetiti da konkavna prizma s minimalnim brojem stranica na bazi ima četverokutni oblik, dok je za konveksnu prizmu to trokutasti oblik.

Poligonalne prizme

Možda je to najpoznatija vrsta klasifikacijskih vrsta prizmi. Trokutaste, četverokutne, peterokutne i tako dalje, prizme će se zvati likovi koji imaju odgovarajući poligon u podnožju. Na primjer, slika prikazuje 6 različitih prizmi - od trokutaste do osmerokutne.

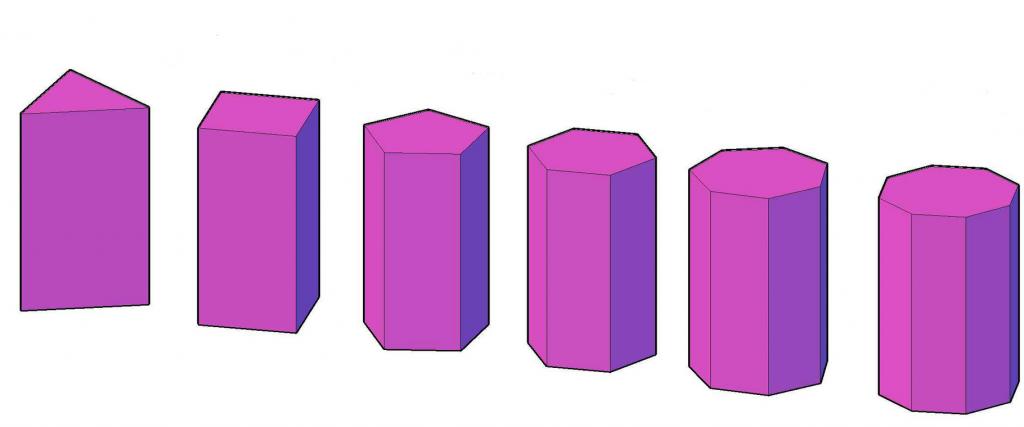
Od svih vrsta poligonalnih prizmi, samo četverokut ima svoje ime - paralelopiped. Potonji, s određenim linearnim i kutnim parametrima, može postati kocka.

Kose i ravne figure

Klasifikacija kosih i izravnih prizmi temelji se na kutovima između dviju strana figure i njegove baze. Ako su svi ti dihedralni kutovi jednaki 90 ^o , tada će se prizma nazvati ravnom ili pravokutnom. Ako barem jedan dihedralni kut nije ispravan, tada se slika smatra kosim ili kosim. Sjetite se da govorimo samo o dihedral angles između baze i strane. Kutovi između dviju strana ne uzimaju se u obzir.

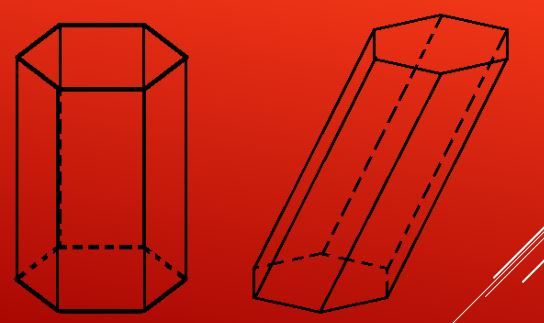
Navedeno pokazuje kako izgledaju nagnute i ravne šesterokutne prizme. Slika prikazuje da su strane prizme pravokutnici (kvadrati). Različiti tipovi izravnih prizmi i kosi mogu se dobiti promjenom broja strana poligona u njihovim bazama.

Pravo i pogrešno

Jednostavno rečeno, ako je prizma ravna i njezina baza je n-gon ispravna, onda će ona također biti točna. Sve ostale prizme koje ne zadovoljavaju opisane uvjete su netočne.

Gornja slika, koja prikazuje šest poligonalnih prizmi, pokazuje pravilne oblike.

Pogodno je proučavati svojstva regularnih prizmi, jer za svaku od njih postoje specifične formule za određivanje njihove visine, površine, volumena, duljine dijagonale i drugih svojstava.

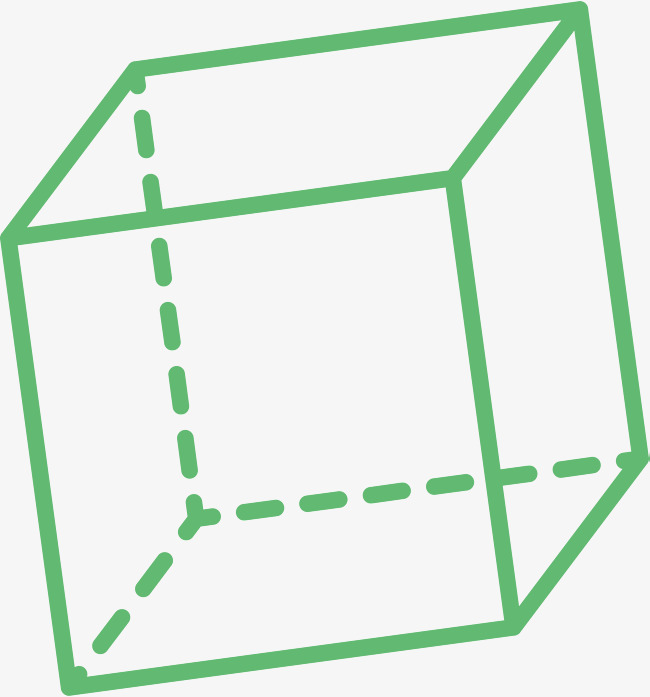
Pravilna četverokutna prizma čija je visina jednaka strani svoje baze, naziva se kocka.

Trokutaste prizme

Osvrnimo se na trokutaste prizme, budući da su one najjednostavnije među razmatranim skupinama figura.

Svaki takav oblik ima 5 lica, 6 jednakih vrhova i 9 rubova. Količine trokutastih prizmi izračunavaju se pomoću formule koja vrijedi za sve prizme. Izgleda kao:

V = S _o * h.

Volumen je jednak proizvodu površine jedne baze i visini slike. U slučaju regularne prizme sa stranom a trokuta, ova formula ima oblik:

V = /3 / 4 * a ² * h.

S obzirom na pitanje o tipovima prizmi, površina trokutastih prizmi definirana je kao zbroj područja dva identična trokuta i tri paralelograma. Ako je to ispravna prizma, tada će vrijediti sljedeća formula za površinu S:

S = /3 / 2 * a ² + 3 * a * h.

Prilikom pisanja ovog izraza koristili smo činjenicu da su u ispravnoj prizmi sve strane jednake jedna drugoj i da su pravokutnici.