Stablo odlučivanja je primjer. Metode odlučivanja

U većini slučajeva, donošenje odluka može se provesti brzinom svjetlosti, na temelju našeg iskustva, kako kažu, okom. Ali ponekad se ova opcija ne smatra adekvatnom. I što učiniti u ovom slučaju? Posebno za ove pametne ljude razvili su metode donošenja odluka. Omogućuju postupno i uz minimalna odstupanja da razrade algoritam djelovanja.

Opće informacije

A najzanimljiviji trenutak za nas je metoda stabla odlučivanja. Kakav je on? Gdje se koristi? Metoda stabla odlučivanja je grafički prikaz određenih radnji i stanja okoliša koji ukazuju na odgovarajuće vjerojatnosti i dobitke za određene kombinacije. Koristi se za procjenu rizika projekata, kada je potrebno uložiti sredstva za značajan vremenski period. Razlog za njegovo korištenje je imati dva ili više skupova uzastopnih rješenja. I trebali bi teći iz prethodnih i / ili skupova stanja okoliša.

O formalnoj strukturi

Koji se elementi koriste za stvaranje? Ovo je:

1. Čvor rješenja. Koristi se za opis trenutka izbora.
2. Linija koja predstavlja alternativu.
3. Čvor događaja Koristi se za označavanje određene slučajnosti koja se događa.
4. Linija koja opisuje okruženje koje je rezultat nepredviđenog događaja.
5. Čvor rezultata. Koristi se za označavanje ukupnih iznosa. Ona je povezana sa specifičnim stanjem okoline i odlukama.
6. Čvor za označavanje srednjeg rezultata. Potrebno je naznačiti situaciju kada treba donijeti drugu odluku.

izgradnja

Kako se metoda stabla odlučivanja koristi u praksi? Za formuliranje različitih scenarija razvoja potrebno je imati sve potrebne i pouzdane informacije, koje uzimaju u obzir vjerojatnosti i vrijeme nastanka određenih događaja i rezultata. U početku se prikupljaju podaci. Da biste to učinili, možete koristiti sljedeći algoritam:

1. Određuje se sastav i trajanje faza životnog ciklusa;
2. Predviđeni su ključni događaji koji će utjecati na (ili će se možda promijeniti) daljnji razvoj;
3. Utvrđuje se vrijeme njihovog pojavljivanja;
4. Formulirana su sva moguća rješenja koja se razmatraju kao opcije za ključne događaje;
5. Utvrđuje se vjerojatnost njihova usvajanja;
6. Procijenjeni troškovi faza u tekućim cijenama.

Na dobivene podatke sasvim je moguće izgraditi stablo odlučivanja. Ona će sadržavati čvorove koji se smatraju ključnim događajima. U biti, to su točke odlučivanja. Pridružuju im se grane - to jest, određena djela koja imaju za cilj postizanje određenog rezultata. Izrada stabla odlučivanja omogućuje izračun vjerojatnosti za svaki odabrani scenarij. Osim toga, pozornost se posvećuje i drugim bitno važnim pokazateljima koji su potrebni za analizu rizika i donošenje učinkovitih upravljačkih aktivnosti. Valja napomenuti da se ova metoda obično koristi za projekte koji imaju više mogućih opcija. Inače, shema postaje preobimna, što otežava izračun optimalnog rješenja i odabir potrebnih podataka. Razumijevanje kako napraviti stablo odlučivanja trebalo bi već formirati. Pogledajmo primjere.

Investicijski projekti

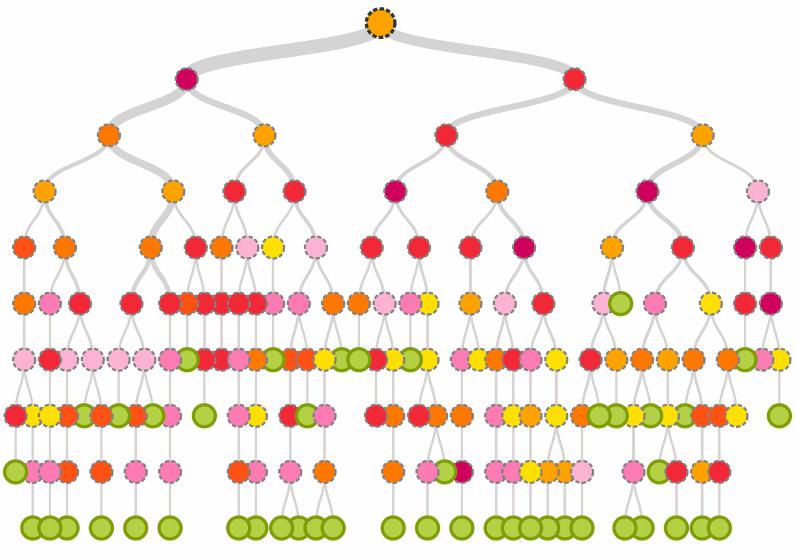
Najbolji način da se razjasni stablo odlučivanja je primjer iz života. Stoga je bolje početi s njom, a ne sa apstraktnom matematikom. Pretpostavimo da imamo izbor od tri investicijska projekta. Označavamo ih kao IP1, IP2 i IP3. Pretpostavimo da za njihovu provedbu potrebno je uložiti 200, 300 i 500 milijuna rubalja. Očekivana dobit je 100, 200 i 300 milijuna rubalja. Postoji rizik od gubitka novca. Vjerojatnost takvog scenarija je 10%, 5% i 20% za svaku od opcija. Što je bolje odabrati? Pronalaženje čisto matematičkog odgovora je vrlo teško. No, uz korištenje stabla odlučivanja, ovaj zadatak je mnogo lakši. U početku je potrebno izraditi stablo odlučivanja o investicijskom projektu. Nakon što smo ga izgradili, počinjemo ga istraživati ​​pomoću obrnute analize. Morate otići na sliku s desna na lijevo. Uzimajući u krug, moramo u njih unijeti matematičke vrijednosti očekivanja plaćanja. U našem slučaju, rezultat će izgledati ovako:

1. 100 x 0,9 - 200 x 0,1 = 70;
2. 200 x 0,95 - 300 x 0,05 = 175;
3. 300 x 0,8 - 500 x 0,2 = 140.

Na temelju izračuna, lako je vidjeti da je IP2 najpovoljniji za nas. A sada ćemo zaroniti u matematiku i razmotriti neke apstraktne probleme na stablu odlučivanja.

Najjednostavniji primjer

U ovom slučaju, imat ćemo samo dvije opcije - "ne" ili "da". Ili, u jeziku Booleove logike, imat ćemo 0 ili 1. Razumijevanje takvog primjera stabla odlučivanja može biti teško, pa ćemo koristiti “ne” ili “da”. Pretpostavimo da nam je ponuđeno raditi za 160 rubalja na sat. Možemo reći ne, i onda se ništa neće promijeniti. Ili kažemo "da", a onda, nakon što smo malo radili, možemo osjetiti kako je u našem džepu postao teži za 160 rubalja. Model možete malo zakomplicirati, au slučaju dogovora dodati nastavak. Na primjer - naporno raditi? Ako "da", onda plaćanje 300 rubalja, ako "ne", onda ostajemo na istoj razini od 160.

Razrada strategija životnog ponašanja

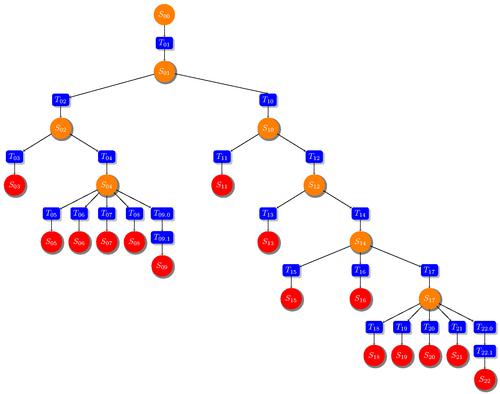
Mnogima se može činiti da se primjer stabla odlučivanja koristi samo za velika ulaganja i apstraktna matematička istraživanja. Ali nije. Naravno, možete zapamtiti teoriju. I možete ga usvojiti i pobijediti. A sada ćemo pogledati formulu koju je Jean-Paul Getty predložio, pod nazivom "Kako postati bogat." Kratko se izražava: "Ustani rano", "Naporno radiš", "Nađi ulje". Pogledajmo modeliranje slijeda odluka:

1. Moramo birati između "Ustani rano" i "Kasni spavanje". To je najjednostavniji izbor.
2. Moramo birati između „Naporno raditi“ i „Nakon rukava“. To je ujedno i najjednostavniji izbor.
3. Istovremeno se događaj "Pronađeno ulje" može pojaviti s određenom vjerojatnošću. Njegova vrijednost ovisi o nizu naših odluka.

Ako nađemo ulje, onda smo postali bogati. Nema pronađenih depozita - to znači da postoje samo gubici, potrošnja na pretragu. A ako spavate kasno i radite bezbrižno, onda ne možete čak ni tražiti naftu. Najpoželjnija opcija je "Rano ustaj" i "Naporno radite".

Tražimo naše ulje

A sada za izračune. Razmatrani primjer stabla odlučivanja bolje je objasniti pomoću tablica. Pretpostavimo da radimo optimalno. Onda naša opcija:

Kao što možete vidjeti, najprofitabilnija opcija nudi prilično dobre izglede. Je li moguće koristiti ovu tablicu u cijelosti da biste vidjeli ovaj primjer? Da, i to nije tako teško kao što se na prvi pogled čini:

Ovaj primjer stabla odlučivanja jasno nam pokazuje da je ključ uspjeha težak posao. Veličina radnog dana može nas približiti cilju obogaćivanja i povećanja veličine države. Iako su, naravno, podaci ovdje prilično generalizirani, ali se nadamo da je opći smjer mišljenja razumljiv.

Poboljšani primjer

Netko bi mogao raspravljati - dobro, stablo odlučivanja je korisno. No, razmatrane opcije su previše pretjerane, a njihovo korištenje u stvarnoj situaciji je prilično problematično. Ovo mišljenje ima pravo postojati, ali samo za one koji nisu razumjeli. Stablo odlučivanja može biti vrlo složeno i fleksibilnije. Stoga ćemo malo poboljšati primjer ulja. I ovaj put moramo uzeti u obzir doigravanje. Pretpostavimo da se sredstva za potragu za naftom troše odmah. Ako pronađemo mineral, onda će se sva ulaganja koja su provedena u istraživanju odmah isplatiti. Prihodi će doći za dvije godine. Kao što možete vidjeti, imamo račune i uplate raštrkane tijekom vremenskog razdoblja. I moramo donijeti sve iznose na raspoloživi novac. Pretpostavimo da je diskontna stopa 20%, onda će naša formula za osobu koja naporno radi i rano ustati izgledati ovako: (0.1 * 10 000 000) / 1.22 + 0.9 (-200 000) = 514 444. Za ostale varijante aktivnosti vrijednosti će biti: 157,222, - 128,555, i - 200,000 rubalja. Slažem se, to je više kao obrazloženje za projekt! Unatoč činjenici da su razine dohotka pale, mogućnost napornog rada i ranog ustajanja i dalje je najučinkovitija. Tada kako spavati do kasno ne privlači. A što je donošenje odluka korisno za nas, i za život i za izračune?

Primjer za zagrijavanje

Nudimo čitateljima da konsolidiraju svoje znanje. Pretpostavimo da imamo doc. On proizvodi proizvode P1 u iznosu od tisuću jedinica. Šef DOK-a smatra da se tržište za robu P2 širi. Provedena su istraživanja koja su omogućila utvrđivanje predloženih razvojnih opcija: P1mak = 1000; Pl = 5000; P2mak = 8000; P2min = 4000. Ovdje min i mak je vjerojatnost potražnje za određenom količinom robe. To jest, tisuću P1 nije problem za implementaciju. Ali 5000 možda neće moći. Vjerojatnost zahtjeva je: C1mak = 0,7; C1min = 1-C1mak = 0,3; S2mak = 0,6; C2min = 1 - C2mak = 0,4. Po jedinici robe P1 ostvarujemo dobit u iznosu od 1 novčane jedinice. Za A2, ova brojka je 0,9. No, tu je problem - minimalna potražnja za oba proizvoda premašuje postojeće i raspoložive kapacitete MKL-a. Koliki će biti troškovi (sada jednaki K) da bi se udvostručili za paralelnu proizvodnju u ekvivalentu, ako:

1. troškovi su K = 0,4 * 103 monetarne jedinice;
2. ekvivalentna količina P1 = 1000, i P2 = 900;
3. maksimalna i trenutna potražnja za P1 i P2 su: (K1mak = 2 * 103; K1min = 1.4 * 103) i (K2mak = 1.2 * 103; K2min = 0.8 * 103).

Uz takve podatke potrebno je odrediti je li preporučljivo zamijeniti proizvedene proizvode i razviti kapacitete.

Rješavanje problema

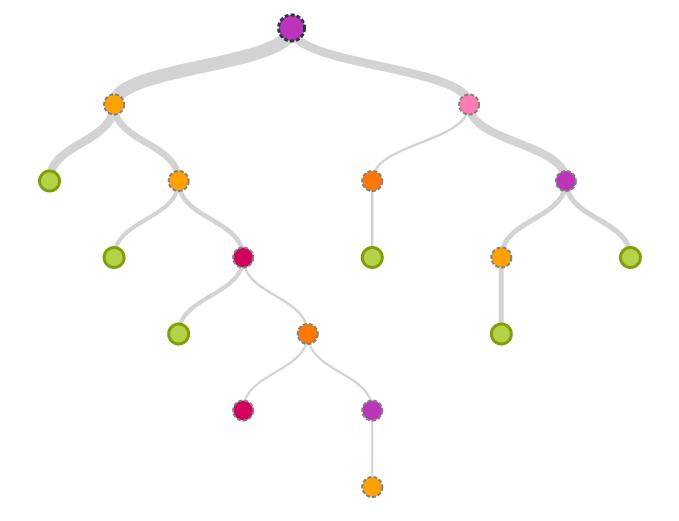
Je li teško sami to shvatiti? Pa, mali savjet - možete koristiti algoritam koji je korišten u primjeru s uljem. Za one koji ga ne mogu ovladati, bit će napisano rješenje. U početku utvrđujemo posljedice naših odluka za proizvodnju jedne vrste (P1 ili P2). Zatim istražite opciju s oba. Da bismo to učinili, odbacujemo iracionalne akcije za razvoj kapaciteta i izdvajamo podatke o mogućim dobitcima odvojeno u stupcu. Mi uzimamo u obzir vjerojatnost potražnje i procjenjujemo prosječnu učinkovitost na granskim točkama. Ako izračunamo, vidjet ćemo da je produžena proizvodnja P1 proizvoda povoljnija za nas u razvoju kapaciteta i istovremene proizvodnje od prijelaza na jedan P2. Iako, to je ako minimalna očekivanja. A što je s maksimalnom potražnjom? U ovom slučaju, moramo nacrtati drugu granu koja će razmotriti ovo rješenje. Da bismo izračunali njegovu učinkovitost, sumiramo prvu i drugu opciju i oduzimamo troškove udvostručenja kapaciteta. I ispada da je to najprofitabilnije rješenje. Kao rezultat toga, došli smo do zaključka da je potrebno razviti kapacitete i osigurati istodobno oslobađanje P1 i P2.

Postavite ciljeve

To je ono što je stablo odlučivanja. Primjeri rješavanja problema rizika omogućuju nam da shvatimo ovu metodu i usvojimo je. Naravno, u početku mogu postojati određene poteškoće, ali se uspješno rješavaju praksom. U tome mogu pomoći knjige iz matematike, ekonometrije, kibernetike i brojnih drugih disciplina.

Sposobnost automatizacije

Metode odlučivanja imaju jasnu strukturu. Dakle, računalne tehnologije mogu vrlo lako raditi s njima. Kao još jedan primjer, proces izdavanja kredita u banci. Istodobno, za računalo, stablo odlučivanja predstavljeno je u obliku logičkog konstrukta "ako ... onda ...". Iako se, usput rečeno, temelji i na ovom načelu i za ljude, ali u interakciji s tehnologijom, potrebno je usredotočiti pozornost na to. Pretpostavimo da je prvi korak pitanje starosti. Ako je osoba mlađa od četrdeset godina, onda pitaju za njegovo obrazovanje i plaće. Više - postoji li kuća. Odgovor je da - izdajemo kredit. Negativno - pitati o razini prihoda. Manje od 20 tisuća rubalja mjesečno - odbijamo. To se radi brzo i učinkovito.

zaključak

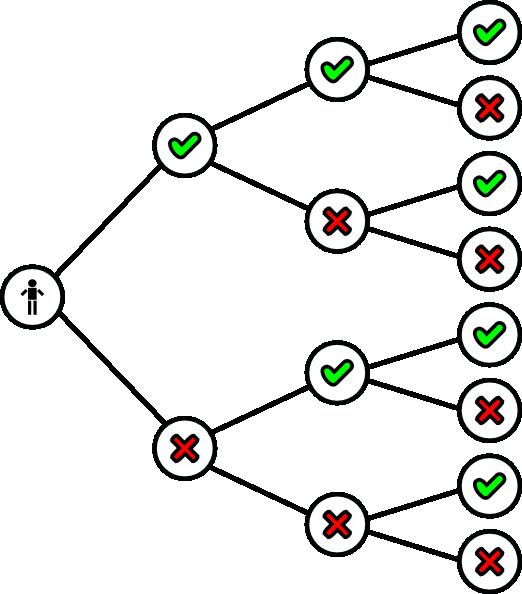
Ako postoji nekoliko ponašanja i scenarija, trebali biste koristiti stablo odlučivanja kako biste pronašli najbolju situaciju. To će omogućiti stavljanje svih dostupnih informacija i izračuna na papir i poboljšati učinkovitost donošenja odluka.