Koje su poteškoće koje čekaju one koji su se obvezali izvršiti dodavanje korijena?

Tema kvadratnog korijenja obvezna je u školskom kurikulumu tečaja matematike. Bez njih, nemojte to učiniti kad odlučujete jednadžbe kvadrata. A kasnije postaje nužno ne samo izvući korijene, nego i izvesti druge akcije s njima. Među njima su dosta složeni: eksponenciranje množenje i podjela. No, tu su vrlo jednostavne: oduzimanje i dodavanje korijena. Usput rečeno, na prvi pogled izgledaju samo tako. Trčanje bez grešaka nije uvijek lako za nekoga tko tek počinje s njima.

Što je matematički korijen?

Ova akcija nastala je u suprotnosti s eksponentom. Matematika pretpostavlja postojanje dvije suprotne operacije. Postoji oduzimanje za zbrajanje. Množenju se suprotstavlja podjela. Inverzni stupanj je vađenje odgovarajućeg korijena.

Ako postoji dva u moći, onda će korijen biti kvadrat. To je najčešće u školskoj matematici. On čak nema ni naznaku da je kvadrat, to jest, broj 2 mu se ne pripisuje, a matematička oznaka za tog operatera (radikala) prikazana je na slici.

Iz opisane akcije glatko slijedi njegova definicija. Za izdvajanje kvadratni korijen iz određenog broja, morate shvatiti što će dati, kada se umnožava u sebe, radikalni izraz. Taj će broj biti kvadratni korijen. Ako ga pišete matematički, dobivate sljedeće: x * x = x ² = y, zatim =u = x.

Što možete učiniti s njima?

U svojoj srži, korijen je frakcijski stupanj, u kojem je jedinica u brojniku. A nazivnik može biti bilo koji. Na primjer, na kvadratnom korijenu, to je jednako dva. Stoga će sve radnje koje se mogu izvoditi s stupnjevima vrijediti za korijene.

A zahtjevi za ove akcije su isti. Ako umnožavanje, podjela i eksponencijacija ne nailaze na poteškoće za studente, dodavanje korijena, kao i njihovo oduzimanje, ponekad dovodi do zabune. I sve zato što želim izvesti ove operacije bez obzira na znak korijena. I ovdje počinju pogreške.

Koja su pravila za njihovo dodavanje i oduzimanje?

Prvo morate zapamtiti dva kategorična "ne":

• ne dodavati i oduzimati korijene, kao prosti brojevi to jest, nije moguće napisati jednostruke znake sumirane radikalne izraze i izvršiti matematičke operacije s njima;
• ne možete dodavati i oduzimati korijene s različitim pokazateljima, kao što su kvadratni i kubični.

Dobar primjer prve zabrane: +6 + ≠10 ≠ √16, ali √ (6 + 10) = .16 .

U drugom slučaju, bolje je da se ograničimo na pojednostavljenje samih korijena. I u odgovoru ostaviti njihov iznos.

Sada prema pravilima

1. Pronađite i grupirajte slične korijene. To jest, oni koji imaju ne samo iste brojeve pod radikalnim, nego i sami imaju isti pokazatelj.
2. Za izvođenje dodavanja korijena, ujedinjenih u jednu skupinu prvom akcijom. Lako je implementirati, jer samo trebate zbrojiti vrijednosti koje stoje ispred radikala.
3. Izvadite korijene u onim terminima u kojima radikalni izraz tvori cijeli kvadrat. Drugim riječima, ne ostavljajte ništa pod znakom radikala.
4. Pojednostavite izraz. Da biste to učinili, morate ih razgraditi u osnovne čimbenike i vidjeti hoće li dati kvadrat bilo kojeg broja. Jasno je da je to istina kada je riječ o kvadratnom korijenu. Kada je eksponent tri ili četiri, tada bi osnovni faktori trebali dati kocku ili četvrtu snagu broja.
5. Uklonite iz množitelja radikalnog znaka, koji daje cijeli stupanj.
6. Pogledajte ponovno pojavljivanje sličnih pojmova. Ako je tako, ponovite drugu radnju.

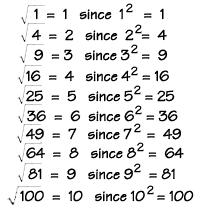
U situaciji kada zadatak ne zahtijeva točnu vrijednost korijena, može se izračunati na kalkulatoru. Beskrajni decimalni dio, koji će biti prikazan u njegovom prozoru, okruglo. Najčešće se to radi za stotinu. Zatim izvršite sve operacije za decimalne frakcije.

Preporuka: nakon razgradnje u osnovne čimbenike, morate provjeriti. To jest, pomnožite ih jedan s drugim i provjerite je li dobivena izvorna vrijednost.

To su sve informacije o tome kako se izvodi dodavanje korijena. Donji primjeri ilustriraju gore navedeno.

Prvi zadatak

Izračunajte vrijednost izraza:

a) +2 + 3√32 + ½ 8128 - 6√18;

b) --75 - 7147 + --48 - 1/5 ;300;

c) 75275 - 10√11 + 2√99 + 6396.

Odluka.

a) Ako slijedite gornji algoritam, jasno je da za prva dva postupka u ovom primjeru nema ničega. Ali možete pojednostaviti neke radikalne izraze.

Na primjer, 32 se dekomponira na dva faktora 2 i 16; 18 će biti jednak proizvodu 9 i 2; 128 je 2 po 64. S obzirom na to, izraz će biti napisan ovako:

+2 + 3√ (2 * 16) + ½ 2 (2 * 64) - 6 √ (2 * 9).

Sada moramo ukloniti iz radikalnog znaka one čimbenike koji daju kvadrat broja. To je 16 = 4 ² , 9 = 3 ² , 64 = 8 ² . Izraz će izgledati ovako:

+2 + 3 * 4√2 + ½ * 8 --2 - 6 * 3√2.

Trebate malo lakše pisati. Da biste to učinili, pomnožite koeficijente ispred znakova korijena:

+2 + 12√2 + 4 --2 - 12√2.

U ovom su se izrazu svi izrazi pokazali sličnima. Stoga, oni samo trebaju odustati. Odgovor će biti: 5√2.

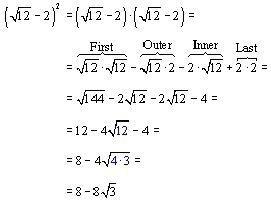
b) Kao i prethodni primjer, dodavanje korijena počinje njihovim pojednostavljenjem. Radikalni izrazi 75, 147, 48 i 300 bit će predstavljeni sljedećim parovima: 5 i 25, 3 i 49, 3 i 16, 3 i 100. Svaki od njih ima broj koji se može ukloniti iz znaka korijena:

5√5 - 7√3 + 4√3 - 1/5 * 10√3.

Nakon pojednostavljenja dobivamo odgovor: 5√5 - 5√3. Može se ostaviti u ovom obliku, ali je bolje uzeti zajednički faktor 5 za zagrade: 5 (√5 - )3).

c) I opet, faktoring: 275 = 11 * 25, 99 = 11 * 9, 396 = 11 * 36. Nakon uklanjanja čimbenika iz znaka korijena, dobivamo:

5√11 - 10√11 + 2 * 3√11 + 6√11. Nakon donošenja takvih uvjeta dobivamo rezultat: 7√11.

Primjer s djelomičnim izrazima

45 (45/4) - --20 - 5√ (1/18) - 1/6 45245 + √ (49/2).

Čimbenici će morati razgraditi sljedeće brojeve: 45 = 5 * 9, 20 = 4 * 5, 18 = 2 * 9, 245 = 5 * 49. Slično onima koje smo već razmatrali, morate ukloniti čimbenike iz znaka korijena i pojednostaviti izraz:

3/2 --5 - 2√5 - 5/3 √ (½) - 7/6 +5 + 7 (½) = (3/2 - 2 - 7/6) --5 - (5/3 - 7 ) √ (½) = - 5/3 +5 + 16/3 √ (½).

Ovaj izraz zahtijeva da se oslobodimo iracionalnosti u nazivniku. Da biste to učinili, pomnožite s /2 / √2 drugi pojam:

- 5/3 +5 + 16/3 √ (½) * /2 / =2 = - 5/3 +5 + 8/3 .2.

Za potpunost djelovanja potrebno je prije korijena odabrati cjelobrojni dio čimbenika. U prvom je jednak 1, u drugom - 2.