Što je načelo farme?
XVII. Stoljeće obilježeno je brzim razvojem u Europi posebnog dijela fizike - optike. Zakoni refleksije i loma bili su otvoreni za svjetlo, a Fermatov princip pokazao je zašto imaju odgovarajući matematički oblik. Pogledajmo detaljnije što je to načelo.
Fenomene loma i refleksije

Razmišljajući, oni razumiju fenomen u kojem se svjetlost, koja se širi u njoj prozirnu tvar, susreće s preprekom na svom putu i drastično mijenja svoju putanju. Bilo koja zapreka može biti bilo koja: tekuća ili čvrsta, prozirna i neprozirna.
Fenomen refleksije poznat je još od antičkih vremena. Prema povijesnim dokazima, zakoni refleksije već su bili formulirani prije naše ere. I u prvom stoljeću poslije Krista egipatski filozof Heron iz Aleksandrije izrazio je ideju o putanji svjetla koju je francuski Pierre Fermat kasnije upotrijebio u formuliranju svog načela.

Fenomen loma je lom ravne linije uz koju se kreće svjetlo, kada prelazi preko površine koja razdvaja dva prozirna materijala. Imajte na umu da se u slučaju refleksije snop kreće u jednom prozirnom materijalu ili, kako se kaže, u jednom mediju.
Prva formulacija zakona loma pripisana je perzijskim matematičarima iz 10. stoljeća izvjesnom Ibnu Sahlu, koji se u svojim djelima oslanjao na djela Klaudija Ptolomeja (1. - 2. stoljeće). Na prijelazu s kraja XVI. - početka XVII. Stoljeća, nizozemski znanstvenik Snell, sumirajući rezultate mnogih eksperimenata sa svjetlošću, formulirao je u matematičkom obliku drugi zakon loma, koji sada nosi njegovo prezime. Snell je dao svoje riječi u smislu udaljenosti, a ne kutova, kao što je sada uobičajeno. Suvremeni izgled zakona loma već je dao Rene Descartes.
Zakoni širenja svjetlosti u prozirnim medijima
Prije nego što pređemo na razmatranje Fermatova načela, treba formulirati zakone loma i refleksije svjetla. Za svaku od tih pojava uobičajeno je izdvojiti dva zakona. Ispod su kombinirani u parovima:
- Putanja grede, kada prelazi granicu između dva medija, uvijek leži u istoj ravnini kao i normala na ravninu te granice. Moguća putanja zraka se formira u općem slučaju iz triju dijelova: upadnog snopa, lomljenog i reflektiranog.
- Ako se kut između snopa upadne svjetlosti i normale naziva θ 1 , isti kut, ali za reflektiranu zraku, upisuje se kao θ 2 , a lomljeni kut je θ 3 , tada će drugi zakon izgledati ovako:
- za refleksiju: θ 1 = θ 2 ;
- za lom: n 1 * sin (θ 1 ) = n 2 * sin (θ 3 ).
U tim formulama, n 1 i n 2 su indeksi loma u prozirnim medijima 1 i 2. Indeks loma, prema definiciji, izračunava se na sljedeći način:
n = c / v.
Ovdje v i c su brzine kretanja svjetlosnog snopa u mediju iu vakuumu.
Formulacija načela farme

Pierre Fermat bio je jedan od najpoznatijih matematičara i pravnika Francuske u prvoj polovici 17. stoljeća. Načelo koje nosi njegovo ime formulirao je 1662., to jest pola stoljeća nakon što je Snell otkrio svoj zakon za refrakciju.
Ukratko, Fermatov princip može se formulirati na sljedeći način: svjetlo, kada se kreće u apsolutno bilo kojem prozirnom mediju, odabire takvu putanju, koju prolazi u najkraćem vremenu.
Zapravo, ova formulacija se ne razlikuje od one koju je Heron iz Aleksandrije učinila jednu i pol tisuću godina ranije za fenomen refleksije. Ipak, Francuz ga je učinio zajedničkim za sve pojave povezane sa svjetlošću i pokazao kako se zakoni loma i refleksije mogu izvesti iz tog načela.
Zaključak 1. Zakona o refleksiji
Koristeći Fermatov princip, zakoni refleksije će se dobiti matematički. Da biste to učinili, razmotrite donju sliku.
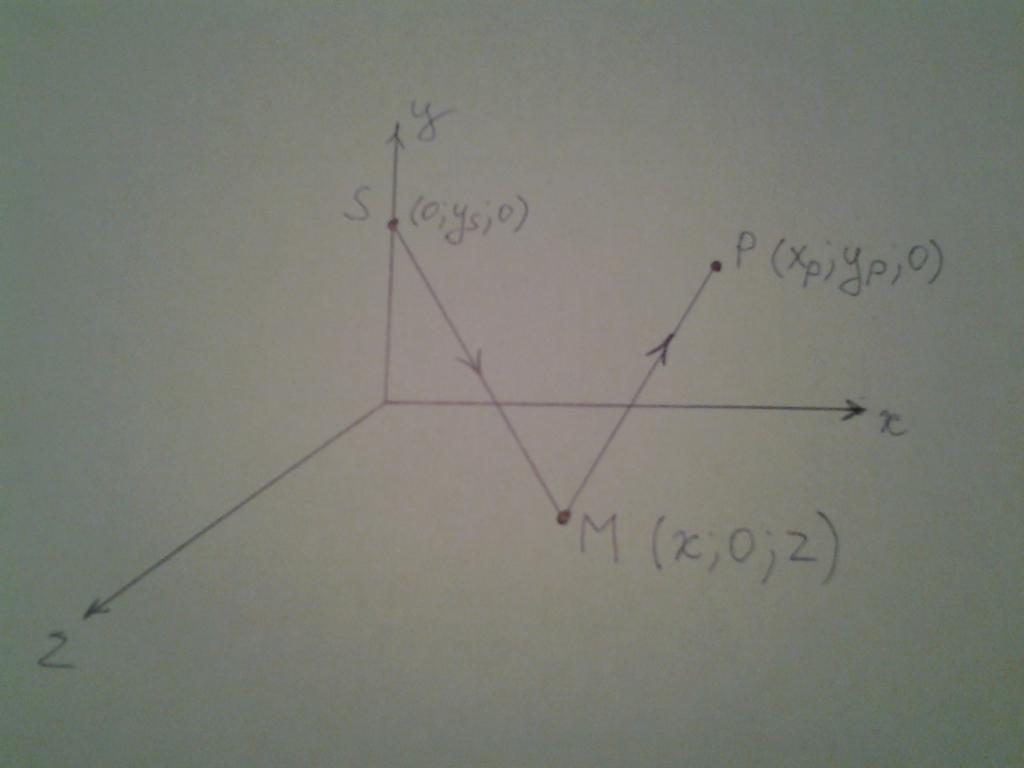
Ovdje se pokazuje da snop izlazi iz točke S, koja leži na y osi. Zatim se reflektira od xz ravnine u nekoj nepoznatoj točki M. Nakon refleksije, snop se seli u točku P koja leži na xy ravnini. Odabrani položaj točaka S i P ne utječe na općenitost daljnjeg rasuđivanja, već samo pojednostavljuje matematičke izračune.
Dakle, zapisujemo koordinate svake točke:
S (0; yS; 0);
M (x; 0; z);
P ( xP ; yP ; 0).
Pozicijske koordinate točaka S i P su poznate. Zadatak je pronaći takvu točku M, koja će odgovarati stvarnoj SMP stazi koja prolazi zrakom svjetlosti. Također pretpostavljamo da je razmatrani prostor homogen, odnosno da je brzina svjetlosti u bilo kojoj točki konstantna vrijednost.
Prema Fermatovom principu, SMP svjetlosna putanja će proći u najkraćem vremenu ako je to najkraće moguće. Pišemo njezinu duljinu:
SM = x (x2 + yS2 + z2); MP = (((xx P ) 2 + yP2 + z2);
SMP = √ (x 2 + y S 2 + z 2 ) + √ ((xx P ) 2 + y P 2 + z 2 ).
Za izračun minimalne SMP duljine potrebno je pronaći parcijalne derivate s obzirom na x i z (nepoznate koordinate točke M) i izjednačiti dobivene rezultate na nulu.
Najprije nalazimo djelomični derivat s obzirom na z. Imamo:
SM (SMP) / =z = z / √ (x 2 + y S 2 + z 2 ) + z / √ ((xx P ) 2 + y P 2 + z 2 ) = 0.
Ta jednakost ima jedan korijen kada je z = 0. Drugim riječima, točka M leži na x osi, tj. U istoj ravnini kao i točke P i S (ravnina xy). Iz čega slijedi da će obnovljena norma na xz ravninu, u kojoj se, pomoću uvjeta problema, nalazi točka M, nalaziti s SM i MP u istoj ravnini (xy). Ovo je prvi zakon refleksije.
Zaključak 2. Zakona o refleksiji
Nastavite izračunavati prethodnu stavku. Kao što je već rečeno, sada je potrebno pronaći djelomični derivat s obzirom na x. Imamo:
SM (SMP) / =x = x / √ (x2 + yS2 + z2) + (xxP) / √ ((xxP) 2 + yP2 + z2) = 0.
Posljednju jednakost napišemo u obliku:
x / SM + (xx P ) / MP = 0 =>
x / SM = (x P -x) / MP.
Odnosi dobiveni u svakom dijelu jednakosti su sinusi kutova s vrhom u točkama S i P. Ako sada vratimo normalu na ravninu xz kroz točku M, tada će označeni kutovi odgovarati kutovima upadanja (između SM i normale) i refleksijama (između MP i normale) i refleksije (između MP i normale) ,
Tako smo, slijedeći Fermatov princip, dobili i drugi zakon refleksije svjetlosti.
Zaključak zakona loma Snella
Pokažimo sada kako se zakon loma svjetlosti može izvesti iz Fermatova načela. Da biste to učinili, razmotrite sliku sličnu prethodnoj.
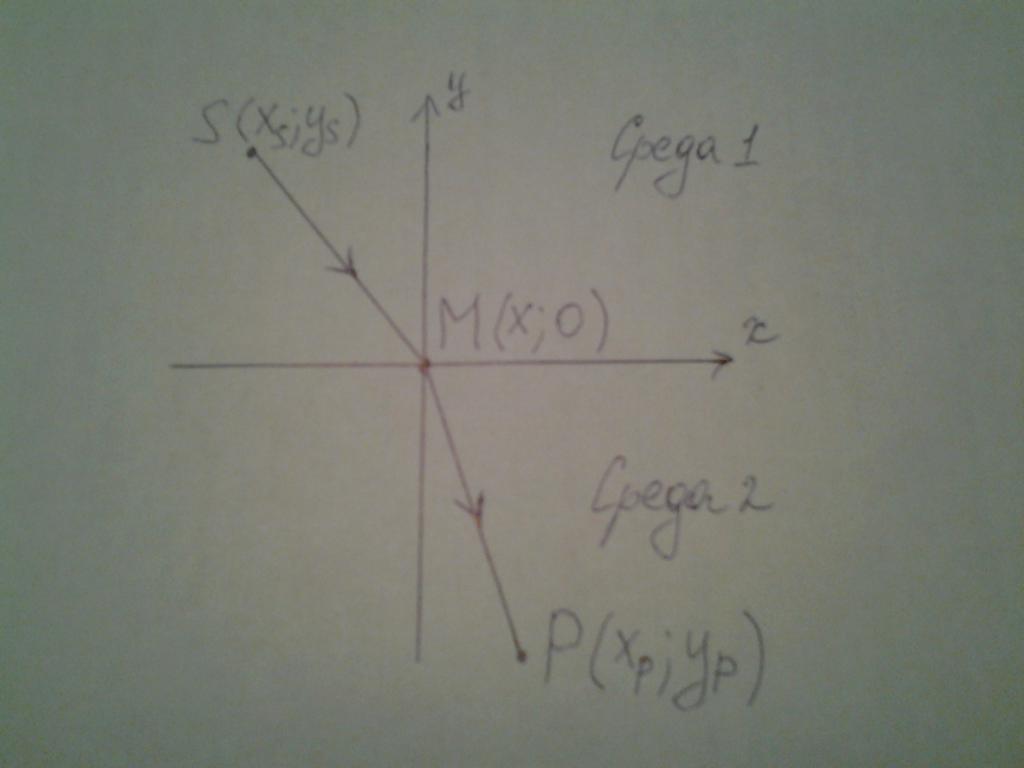
Radi jednostavnosti, razmotrit ćemo slučaj u xy ravnini. Zapisujemo koordinate izvora S i prijemnika P svjetlosti koje se nalaze u različitim okruženjima:
S (xS; yS);
M (x; 0);
P ( xP ; yP ).
Nađimo nepoznatu koordinatu točke M. Koordinata y = 0 je za nju točno poznata, jer se upravo na granici medija (x osi) mijenja brzina svjetlosti. Duljine segmenata SM i MP jednake su:
SM = x (xx S ) 2 + yS2);
MP = x (xP-x) 2 + yP2).
Ukupno vrijeme koje svjetlo troši na SMP putanju bit će jednako:
t = SM / v1 + MP / v2.
Ovdje v1 i v2 su brzine zraka u odgovarajućem mediju. Da bismo pronašli minimalno vrijeme gibanja, treba uzeti ukupni derivat s obzirom na varijablu x i izjednačiti ga s nulom. Dobivamo:
dt / dx = (xx S ) / (√ (xx S ) 2 + y S 2 ) * v 1 ) - (x P -x) / (√ (x P -x) 2 + y P 2 ) * v 2 ) = 0 =>
(xx S ) / (SM * v 1 ) = (x P -x) / (MP * v2).
Koristeći funkcije sinusa kuta upada θ 1 i refrakcije θ 3 , dobivamo:
sin (θ 1 ) / v 1 = sin (θ 3 ) / v 2 .
Da bi se dobivena jednakost Snellovom zakonu dovela u prikladnom obliku (preko indeksa loma medija), potrebno je pomnožiti lijevu i desnu stranu brzinom svjetlosti c.

Stoga primjena Fermatova načela olakšava zaključivanje zakona za glavne pojave gibanja svjetlosnog snopa u transparentnim materijalima.
Kretanje svjetla u nehomogenom mediju
Gore navedeni slučajevi pretpostavljaju da je materijal homogen i da svjetlosna zraka zadržava svoju brzinu kada se pomiče. U slučaju nehomogenih medija vrijedi sljedeća jednakost:
L = (n (x, y, z) * dl.
Taj se integral uzima duž putanje svjetla. Diferencijal dl je segment puta za koji medij zadržava svoju homogenost. Vrijednost n (x, y, z) je lokalni indeks loma.
Zabilježeni integral obično se naziva integralni optički put. Načelo farme za optički put uključuje pronalaženje ekstrema za L.
Općenita formulacija razmatranog načela
Princip minimalnog vremena za kretanje svjetla je poseban za općenitiju formulaciju. Trenutno, Fermatov generalizirani princip je formuliran na sljedeći način: svjetlo odabire putanju tijekom kretanja koja odgovara ekstremima optičkog puta.
Ekstremi funkcije, prema matematičkoj definiciji, su minimalna, maksimalna i točka infleksije. Opći princip Fermata zadovoljava sve ove vrijednosti, tj. Putanja svjetlosti ne mora nužno biti minimalna, može biti i maksimalna i odgovarajuća točka infleksije optičkog puta.
Domaća analogija s razmatranim načelom
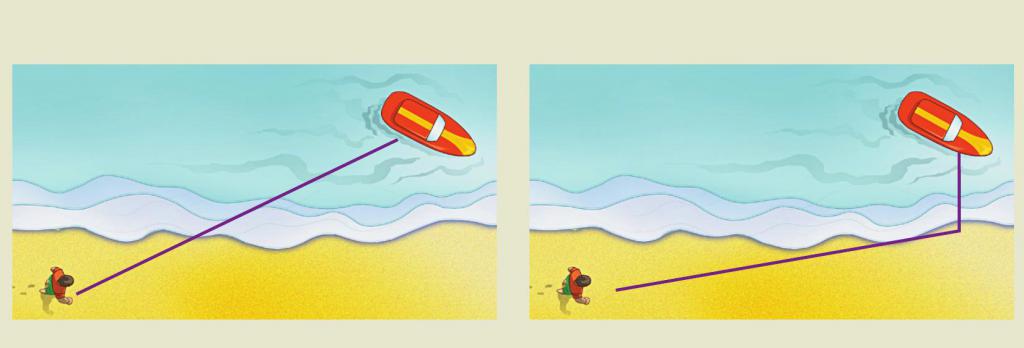
Opći princip Fermata je pak poseban slučaj tzv. Principa najmanjeg djelovanja. Ovdje nećemo dati odgovarajuće definicije i njihove matematičke formulacije, međutim, pokazat ćemo gdje se može primijeniti princip koji su predložili Francuzi.
Koristi se u rješavanju jednostavnog, na prvi pogled, svakodnevnog zadatka: na primjer, osoba se utapa u moru u blizini plaže. Kako bi se spasilac trebao pomaknuti na obalu kako bi spasio utopljenika? Naravno, on bi trebao doći u pomoć najmanje vremena. Budući da je brzina kretanja spasioca na plaži veća nego na vodi, trebao bi proći neku udaljenost duž obale, a tek onda skočiti u vodu i plivati. To jest, zadatak je sveden na primjenu principa Fermata, gdje ulogu svjetlosnog snopa igra spasitelj.
Imajte na umu da rješenje ovog problema nije jednostavno, jer se u njegovom procesu pojavljuju jednadžbe četvrtog stupnja.
Stoga je Fermatov princip alat za dobivanje osnovnih zakona širenja svjetla. Međutim, to nije temeljno. Može se reći da slijedi iz Huygensovog principa izvora sekundarnih sfernih valova.