Sve mogućnosti kako pronaći trapezoidno područje
Mnogostran trapez ... Može biti proizvoljan, jednakokračan ili pravokutan. I u svakom slučaju, morate znati kako pronaći područje trapeza. Naravno, najlakši način za pamćenje osnovnih formula. Ali ponekad je lakše upotrijebiti onu koja je izvedena sa svim značajkama pojedinca geometrijski oblik.
Nekoliko riječi o trapezu i njegovim elementima
Bilo koji četverokut čije su dvije strane paralelne može se nazvati trapezom. Općenito, oni nisu jednaki i nazivaju se osnovama. Veći od njih je niži, a drugi je gornji.
Druge dvije strane su bočne. Za proizvoljni trapez, oni imaju različite duljine. Ako su jednaki, onda ta figura postaje jednakokračna.
Ako je kut između bilo koje strane i baze iznenada 90 stupnjeva, trapez je pravokutan.
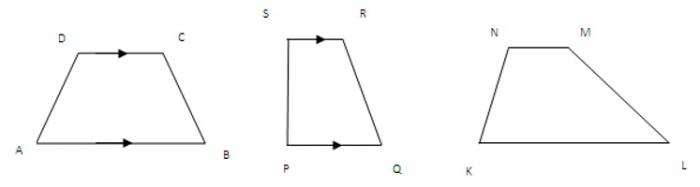
Sve ove značajke mogu pomoći u rješavanju problema kako pronaći područje trapeza.
Među elementima figure koji mogu biti neophodni u rješavanju problema, možemo istaknuti sljedeće:
- visina, tj. segment okomit na obje baze;
- srednju liniju, koja sa svojim krajevima ima srednju stranu.
Po kojoj formuli izračunati područje, ako znate osnovicu i visinu?
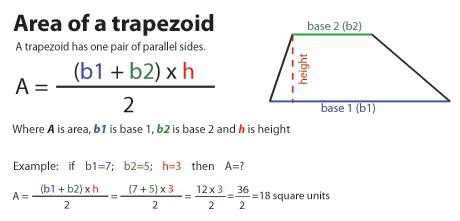
Ovaj izraz daje glavni, jer te vrijednosti najčešće možete prepoznati, čak i ako nisu izričito navedene. Dakle, razumjeti kako pronaći trapezno područje morat ćete sklopiti obje baze i podijeliti ih na dvije. Rezultirajuća vrijednost se tada množi s vrijednošću visine.
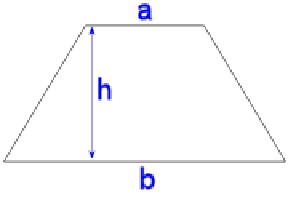
Ako bazu označimo slovima 1 i 2 , visina je n, tada će formula za područje izgledati ovako:
S = ((a 1 + a 2 ) / 2) * n.
Formula za izračunavanje površine, ako je navedena njezina visina i srednja crta
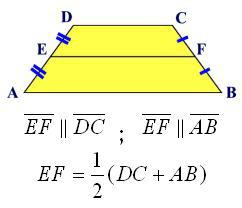
Ako bolje pogledate prethodnu formulu, lako je uočiti da je vrijednost srednje linije jasno prisutna u njoj. Naime, zbroj baza podijeljen s dva. Neka srednja linija bude označena slovom l, tada će formula za područje biti ovako:
S = l * n.
Sposobnost pronalaženja područja dijagonalno
Ova metoda će vam pomoći ako znate kut koji su stvorili. Pretpostavimo da su dijagonale označene slovima q 1 i g 2 , a kutovi između njih su α i β. Tada će se formula kako pronaći područje trapeza napisati na sljedeći način:
S = ((d 1 * d 2 ) / 2) * sin α.
U ovom izrazu, lako možete zamijeniti α s β. Rezultat se neće promijeniti.
Kako saznati područje ako su sve strane slike poznate?
Postoje i situacije kada su upravo te strane poznate na toj slici. Ova formula je glomazna i teška za pamćenje. Ali moguće je. Neka strane imaju oznaku: u 1 i 2 , bazu i 1 više od 2 . Tada će formula područja izgledati ovako:
S = ((a 1 + a 2 ) / 2) * √ {u 1 2 - [(a 1 - a 2 ) 2 + u 1 2 - u 2 2 ) / (2 * (a 1 - a 2 )) ] 2 }.
Načini izračunavanja površine jednakostraničnog trapeza
Prvi se odnosi na činjenicu da se u nju može ući krug. I, znajući njegov radijus (označen je slovom r), kao i kut u bazi - γ, možete koristiti sljedeću formulu:
S = (4 * r2) / sin γ.
Potonja opća formula, koja se temelji na poznavanju svih strana slike, bit će znatno pojednostavljena zbog činjenice da strane imaju isto značenje:
S = ((a 1 + a 2 ) / 2) * √ {u 2 - [(a 1 - a 2 ) 2 / (2 * (a 1 - a 2 ))] 2 }.
Metode za izračun površine pravokutnog trapeza
Jasno je da će bilo koji od navedenih za proizvoljan oblik to učiniti. Ali ponekad je korisno znati za jednu osobinu takvog trapeza. Ona leži u činjenici da je razlika kvadrata duljina dijagonala jednaka razlici koja se sastoji od kvadrata baza.
Često se formule za trapezoid zaboravljaju, a izrazi za područja pravokutnika i trokuta se pamte. Tada možete primijeniti jednostavan način. Podijelite trapezoid u dva oblika, ako je pravokutan, ili tri. Jedan točno će biti pravokutnik, a drugi ili dva preostala trokuta. Nakon izračunavanja područja tih podataka samo će ih dodati.
Ovo je prilično jednostavan način kako pronaći kvadrat trapez.
Što ako su poznate koordinate vrhova trapeza?
U tom slučaju morat ćete upotrijebiti izraz koji vam omogućuje da odredite udaljenost između točaka. Može se primijeniti tri puta: kako bi saznali obje baze i jednu visinu. I onda samo primijenite prvu formulu, koja je opisana malo više.
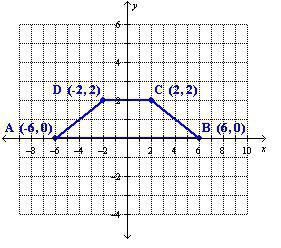
Da bi ilustrirali ovu metodu, možete dati primjer. S obzirom na tocke s koordinatama A (5; 7), B (8; 7), C (10; 1), D (1; 1). Trebate znati područje slike.
Prije nego što pronađete područje trapeza, potrebno je izračunati duljinu baze pomoću koordinata. Trebat će vam sljedeća formula:
duljina segmenta = √ {(razlika prvih koordinata točaka) 2 + (razlika drugih koordinata točaka) 2 }.
Gornja baza označena je s AB, što znači da će njezina duljina biti jednaka √ {(8-5) 2 + (7-7) 2 } = =9 = 3. Niža će biti SD = √ {(10-1) 2 + (1-1) ) 2 } = =81 = 9.
Sada morate držati visinu od vrha do baze. Neka njegov početak bude u točki A. Kraj segmenta će biti na donjoj bazi u točki s koordinatama (5; 1), neka bude točka N. Duljina segmenta AN će biti jednaka √ {(5-5) 2 + (7-1) 2 } = =36 = 6.
Ostaje samo zamijeniti dobivene vrijednosti formuli trapezoidne površine:
S = ((3 + 9) / 2) * 6 = 36.
Problem je riješen bez jedinica, jer koordinatna mreža nije specificirana. Može biti ili milimetar ili metar.
Primjeri zadataka
№ 1. Stanje. Poznati kut između dijagonala proizvoljnog trapeza, jednak je 30 stupnjeva. Manja dijagonala je 3 dm, a druga 2 puta veća. Potrebno je izračunati površinu trapeza.
Odluka. Prvo morate znati duljinu druge dijagonale, jer bez toga ne možete računati na odgovor. Izračunajte ga lako, 3 * 2 = 6 (dm).
Sada morate koristiti odgovarajuću formulu za područje:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4.5 (dm 2 ). Problem riješen.
Odgovor: površina trapeza je 4,5 dm 2 .
№ 2. Stanje. U trapezu AVSD, baze su AD i BC segmenti. Točka E je sredina strane SD-a. Iz njega je izvučena okomita na pravac AB, kraj tog segmenta označen je slovom N. Poznato je da su duljine AB i EH 5 i 4 cm, te je potrebno izračunati površinu trapeza.
Odluka. Prvo morate napraviti crtež. Budući da je vrijednost okomice manja od strane na koju se vodi, trapez će biti lagano ispružen prema gore. Dakle, EN će biti unutar slike.
Da biste jasno vidjeli napredak zadatka, morat ćete izvršiti dodatnu izgradnju. Naime, nacrtajte pravac koji će biti paralelan sa stranom AB. Točke presijecanja ove crte s AD - P, te s nastavkom Oružanih snaga - X. Rezultat je paralelogram. Štoviše, njegovo područje jednako je željenom. To je zbog činjenice da su trokuti koji su ispali s dodatnom konstrukcijom jednaki. To proizlazi iz jednakosti bočne strane i dva ugla susjedna njemu, jednog - okomitog, drugog - u križnom smjeru.
Pronalaženje područja paralelograma moguće je pomoću formule koja sadrži proizvod bočne i visine, spuštene na nju.
Tako je površina trapeza 5 x 4 = 20 cm2.
Odgovor: S = 20 cm 2 .
3. Stanje. Elementi jednakostožilnog trapeza imaju sljedeća značenja: donja baza je 14 cm, gornja je 4 cm, a akutni je 45º. Potrebno je izračunati njegovo područje.
Odluka. Neka manja baza bude označena kao BC. Visina izvučena iz točke B će se zvati HV. Budući da je kut 45º, trokut ABH će biti pravokutan i jednakokračan. Dakle, AN = BH. Osim toga, NA je vrlo lako pronaći. Ona je jednaka polovici osnovne razlike. To je (14 - 4) / 2 = 10/2 = 5 (cm).
Razlozi su poznati, visina se računa. Možete koristiti prvu formulu, koja je ovdje razmatrana za proizvoljni trapezoid.
S = ((14 + 4) / 2) x 5 = 18/2 x 5 = 9 x 5 = 45 (cm2).
Odgovor: Potrebna površina je 45 cm 2 .
№ 4. Stanje. Tu je i proizvoljni trapezoidni AVSD. Na njegovim stranama uzimaju se točke O i E, tako da je OE paralelan s dnom kovčega. Površina trapeznog AOED-a je pet puta veća od površine CFE-a. Izračunajte OE vrijednost ako su osnovne duljine poznate.
Odluka. Bit će potrebno nacrtati dvije paralelne AB ravne linije: prvo kroz točku C, njezino sjecište s OE je točka T; drugi kroz E i sjecište s AD bit će M.
Neka nepoznata OE = x. Visina manjeg trapeza CFE je n 1 ;
Budući da su područja ova dva trapeza povezana kao 1 do 5, možemo napisati sljedeću jednakost:
(x + a 2 ) * n 1 = 1/5 (x + a 1 ) * n 2
ili
n 1 / n 2 = (x + a 1 ) / (5 (x + a 2 )).
Visine i strane trokuta su proporcionalne konstrukciji. Stoga možemo napisati još jednu jednakost:
n 1 / n 2 = (x - a 2 ) / (a 1 - x).
U posljednja dva unosa na lijevoj strani postoje jednake vrijednosti, tako da možete napisati da je (x + a 1 ) / (5 (x + a 2 )) jednako (x - a 2 ) / (a 1 - x).
To zahtijeva niz transformacija. Prvo umnožite poprečno. Pojavit će se zagrade koje označavaju razliku u kvadratima, a nakon primjene ove formule dobit ćete kratku jednadžbu.
U njemu morate otvoriti zagrade i premjestiti sve pojmove iz nepoznatog "x" na lijevu stranu, a zatim izvaditi kvadratni korijen.
Odgovor : x = √ {(a 1 2 + 5 a 2 2 ) / 6}.