Koeficijent korelacije i uzročni odnos: formule i njihovo tumačenje
Koeficijent korelacije je stupanj povezanosti dvije varijable. Njegov izračun daje ideju o tome postoji li ovisnost između dva niza podataka. Za razliku od regresije, korelacija ne dopušta predviđanje vrijednosti veličina. Međutim, izračun koeficijenta važan je korak u preliminarnoj statističkoj analizi. Primjerice, utvrdili smo da je koeficijent korelacije između razine izravnih stranih ulaganja i stope rasta BDP-a visok. To nam daje ideju da je za osiguranje dobrobiti potrebno stvoriti povoljnu klimu za strane poduzetnike. Ne tako očigledan zaključak na prvi pogled!
Korelacija i uzročnost
Možda ne postoji niti jedno područje statistike koje bi bilo tako čvrsto utemeljeno u našem životu. Koeficijent korelacije koristi se u svim područjima javnog znanja. Glavna opasnost leži u činjenici da se njegove visoke vrijednosti često spekuliraju kako bi se uvjerili ljudi i uvjerili ih u neke zaključke. Međutim, zapravo, jaka korelacija uopće ne ukazuje na uzročnu vezu između količina.
Koeficijent korelacije: Pearsonova i Spearmanova formula
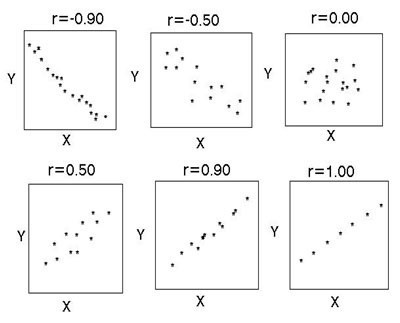
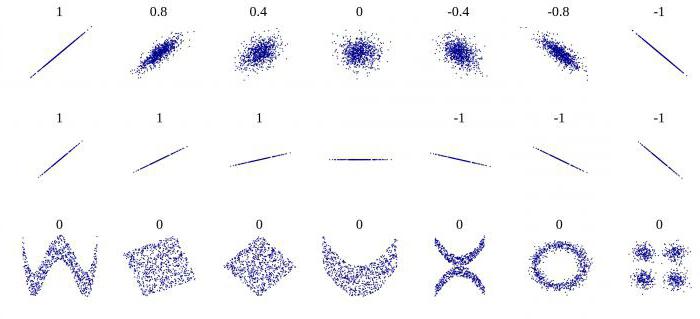
Postoji nekoliko ključnih pokazatelja koji karakteriziraju odnos između dvije varijable. Povijesno gledano, prvi je Pearsonov koeficijent linearne korelacije. Još je u školi. Razvili su ga C. Pearson i J. Yul na temelju djela Fr. Galton. Ovaj koeficijent omogućuje vam da vidite odnos između racionalnih brojeva koji se racionalno mijenjaju. Uvijek je veći od -1 i manji od 1. Negativan broj označava obrnuto proporcionalnu ovisnost. Ako je koeficijent nula, onda ne postoji veza između varijabli. Jednako pozitivnom broju - postoji proporcionalna veza između ispitivanih veličina. Spearmanov koeficijent korelacije ranga omogućuje vam pojednostavljenje izračuna izgradnjom hijerarhije vrijednosti varijabli.
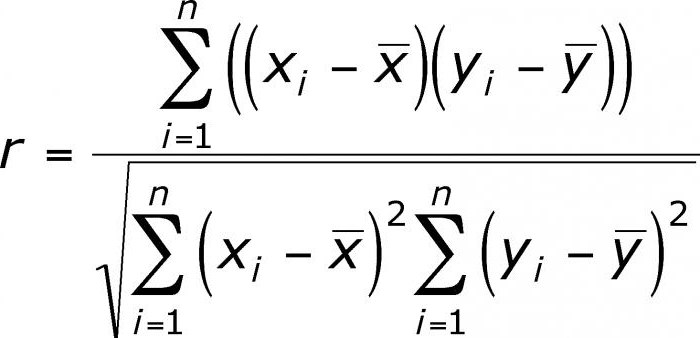
Odnos između varijabli
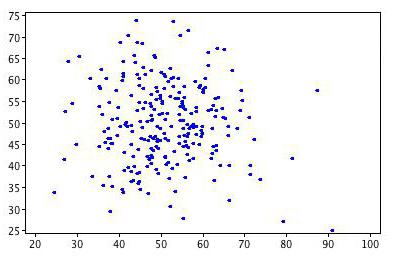
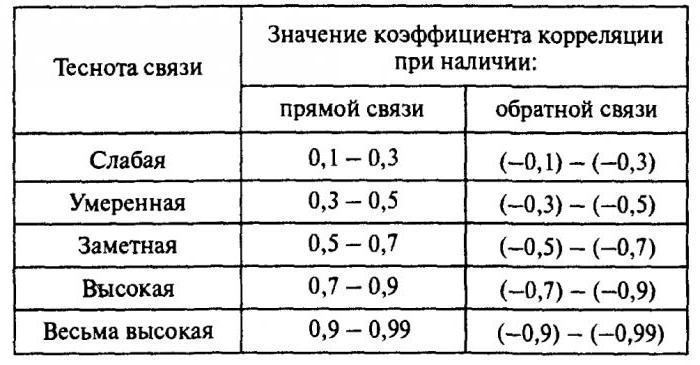
Korelacija pomaže pronaći odgovor na dva pitanja. Prvo, je li odnos između varijabli pozitivan ili negativan. Drugo, koliko je jaka ovisnost. Korelacijska analiza je moćan alat pomoću kojeg možete dobiti ovu važnu informaciju. Lako je vidjeti da obiteljski prihodi i rashodi padaju i raste proporcionalno. Taj se odnos smatra pozitivnim. Naprotiv, s rastom cijena roba potražnja za njom pada. Takva se veza naziva negativna. Vrijednosti koeficijenta korelacije su u rasponu od -1 do 1. Nula znači da ne postoji veza između vrijednosti koje se istražuju. Što je indikator bliži ekstremnim vrijednostima, jača je veza (negativna ili pozitivna). Odsutnost ovisnosti označena je koeficijentom od -0,1 do 0,1. Potrebno je shvatiti da takva vrijednost pokazuje samo odsustvo linearne veze.
Značajke aplikacije
Korištenje oba pokazatelja podložno je određenim pretpostavkama. Prvo, postojanje jake veze ne implicira činjenicu da jedna veličina određuje drugu. Možda postoji i treća količina koja definira svaku od njih. Drugo, visoki Pearsonov koeficijent korelacije ne ukazuje na uzročnu vezu između varijabli koje se istražuju. Treće, pokazuje samo linearnu ovisnost. Korelacija se može koristiti za procjenu značajnih kvantitativnih podataka (na primjer, atmosferskog tlaka, temperature zraka), a ne kategorija kao što su spol ili omiljena boja.
Koeficijent višestruke korelacije
Pearson i Spearman istraživali su odnos između dviju varijabli. Ali kako djelovati u slučaju da postoje tri ili čak više. Ovdje spašava koeficijent višestruke korelacije. Na primjer, na bruto nacionalni proizvod ne utječe samo izravna strana ulaganja ali i monetarne i fiskalna politika kao i razinu izvoza. Stopa rasta i obujam BDP-a rezultat su interakcije niza čimbenika. Međutim, treba razumjeti da se model višestruke korelacije temelji na brojnim pojednostavljenjima i pretpostavkama. Prvo, isključena je multikolinearnost među količinama. Drugo, pretpostavlja se da je odnos između ovisnih i varijabli koje utječu na njega linearan.
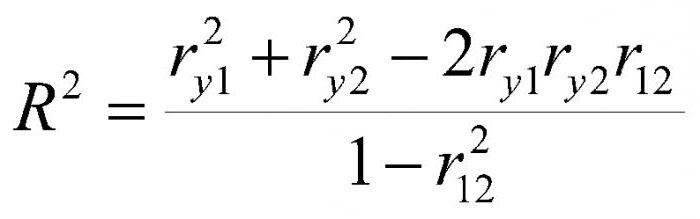
Područja primjene korelacijske i regresijske analize
Ova metoda pronalaženja odnosa među količinama naširoko se koristi u statistici. Najčešće se koristi u tri glavna slučaja:
- Ispitati uzročnu vezu između vrijednosti dvije varijable. Kao rezultat toga, istraživač se nada da će pronaći linearni odnos i izvući formulu koja opisuje te odnose između veličina. Jedinice njihovih mjerenja mogu biti različite.
- Za provjeru veze između vrijednosti. U ovom slučaju, nitko ne određuje koja je varijabla ovisna. Može se ispostaviti da vrijednost obje količine uzrokuje neki drugi faktor.
- Izvesti jednadžbu. U tom slučaju možete jednostavno zamijeniti brojeve u njemu i pronaći vrijednosti nepoznate varijable.
Čovjek koji traži uzročnost
Svijest je uređena na takav način da svakako trebamo objasniti događaje koji se događaju okolo. Osoba uvijek traži vezu između slike svijeta u kojem živi i informacija koje prima. Često mozak stvara red iz kaosa. Lako može vidjeti uzročnu vezu tamo gdje je nema. Znanstvenici moraju posebno naučiti prevladati taj trend. Sposobnost procjene odnosa između podataka objektivno je potrebna u akademskoj karijeri.
Pristrasnost medija
Razmotrite kako se prisutnost korelacijske veze može pogrešno protumačiti. Skupina britanskih učenika s lošim ponašanjem pitali su se jesu li njihovi roditelji pušili. Tada je test objavljen u novinama. Rezultat je pokazao jaku povezanost između pušenja roditelja i prijestupa njihove djece. Profesor koji je vodio studiju čak je sugerirao stavljanje upozorenja na pakete cigareta. Međutim, s ovim zaključkom postoje brojni problemi. Prvo, korelacija ne pokazuje koja je od količina neovisna. Stoga se može pretpostaviti da je ovisnost roditelja uzrokovana neposlušnošću djece. Drugo, nemoguće je sa sigurnošću reći da se oba problema nisu pojavila zbog nekog trećeg faktora. Na primjer, obitelji s niskim primanjima. Treba naglasiti emocionalni aspekt početnih nalaza profesora koji je proveo studiju. Bio je gorljivi protivnik pušenja. Stoga ne čudi da je rezultate svog istraživanja interpretirao na ovaj način.
nalazi
Pogrešno tumačenje korelacije kao uzročnog odnosa između dvije varijable može uzrokovati sramotne pogreške u istraživanju. Problem je u tome što leži u samoj srži ljudske svijesti. Mnogi marketinški trikovi temelje se na ovoj posebnoj značajki. Razumijevanje razlike između uzročnosti i korelacije omogućuje racionalnu analizu informacija iu svakodnevnom životu iu profesionalnoj karijeri.