Kako izračunati granice sekvenci?

Matematika je znanost koja gradi svijet. Kao znanstvenik i jednostavna osoba - nitko ne može bez nje. Prvo, djeca uče računati, zatim zbrajati, oduzimati, množiti i dijeliti, u srednjoj školi se pojavljuju oznake, au starijoj ne mogu bez njih.

Ali danas ćemo govoriti o onome na čemu se temelji sva poznata matematika. Na zajednici brojeva koji se nazivaju "ograničenja slijeda".

Što su sekvence i gdje je njihova granica?

Značenje riječi "slijed" nije teško protumačiti. To je konstrukcija stvari u kojima je netko ili nešto uređeno u određenom redoslijedu ili u redu. Na primjer, red za ulaznice u zoološki vrt - je slijed. I to može biti samo jedan! Ako, na primjer, pogledati red u trgovini - to je jedan slijed. A ako jedna osoba iznenada napusti ovu liniju, onda je ovo druga linija, drugi red.

Riječ "granica" također se lako tumači - to je kraj nečega. Međutim, u matematici, granice sekvenci su one vrijednosti na brojevnoj liniji na koje teži niz brojeva. Zašto traži, a ne završava? Sve je jednostavno, brojčana crta nema kraja, a većina sekvenci, poput zraka, imaju samo početak i izgledaju ovako:

x ₁ , x ₂ , x ₃ , ... x _n ...

Stoga je definicija slijeda funkcija prirodnog argumenta. Jednostavnije rečeno, riječ je o nizu članova nekog skupa.

Kako je izgrađen numerički slijed?

Najjednostavniji primjer numeričkog niza može izgledati ovako: 1, 2, 3, 4, ... n ...

U većini slučajeva, za praktične svrhe, sekvence su izgrađene iz brojeva, a svaki sljedeći član serije, označen s X, ima svoje ime. Na primjer:

x ₁ - prvi član sekvence;

x ₂ - drugi član sekvence;

x ₃ - treći član;

...

x _n je n-ti pojam.

U praktičnim metodama, slijed je dan općom formulom, u kojoj postoji neka varijabla. Na primjer:

X _n = 3n, tada će brojni niz izgledati ovako:

x ₁ = 3;

x2 = 6;

x3 = 9;

i tako dalje

Ne zaboravite da u općem zapisu nizova možete koristiti bilo koja latinična slova, a ne samo X. Na primjer: y, z, k, itd.

Aritmetička progresija kao dio sekvenci

Prije nego što potražimo granice sekvenci, preporučljivo je dublje uroniti u sam koncept takvog numeričkog niza, na koji su se svi susreli u srednjoj klasi. Aritmetička progresija je niz brojeva u kojima je razlika između susjednih članova konstantna.

Zadatak: “Neka je a ₁ = 15, a korak napredovanja numeričkog niza d = 4. Izgradite prvih 4 člana ove serije. "

Rješenje: a ₁ = 15 (po uvjetu) - prvi član progresije (serija brojeva).

a ₂ = 15 + 4 = 19 je drugi član progresije.

i ₃ = 19 + 4 = 23 - treći član.

a ₄ = 23 + 4 = 27 je četvrti član.

Međutim, ovu metodu je teško postići velike vrijednosti, kao što je ₁₂₅ .. Posebno za takve slučajeve izvedena je formula prikladna za praksu: a _n = a ₁ + d (n - 1). U ovom slučaju, a ₁₂₅ = 15 + 4 (125-1) = 511.

Vrste sekvenci

Većina sekvenci su beskrajne, vrijedno pamćenja za cijeli život. Postoje dvije zanimljive vrste brojevnih serija. Prvi je dan formulom a _n = (- 1) ⁿ . Matematičari taj slijed često nazivaju bljeskalicom. Zašto? Provjerite brojčane nizove.

-1, 1, -1, 1, -1, 1, itd. S takvim primjerom postaje jasno da se brojevi u sekvencama mogu lako ponoviti.

Faktorski slijed. Lako je pogoditi - u formuli je prisutan faktorijal koji definira slijed. Na primjer: a _n = (n + 1)!

Zatim će slijed izgledati ovako:

a ₁ = 1x2 = 2;

a2 = 1x2x3 = 6;

a ₃ = 1x2x3x4 = 24, itd.

Slijed definiran aritmetičkom progresijom naziva se beskonačno smanjivanje ako se nejednakost -1 promatra za sve njene članove. n = (–1/2) ⁿ .

a ₁ = - ½;

a2 = ¼;

a ₃ = - 1/8, itd.

Postoji čak i niz koji se sastoji od istog broja. Dakle, i _n = 6 se sastoji od beskonačnog skupa šestica.

Određivanje ograničenja slijeda

Granice sekvenci već dugo postoje u matematici. Naravno, zaslužili su vlastiti kompetentni dizajn. Dakle, vrijeme je da naučite definiciju granica sekvenci. Prvo, detaljno razmotrite granicu za linearnu funkciju:

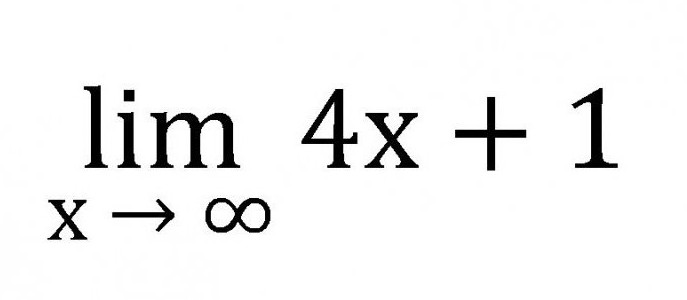
1. Sve granice su skraćeno lim.
2. Ograničenje zapisa sastoji se od kratice lim, neke varijable koje teže određenom broju, nuli ili beskonačnosti, te također iz same funkcije.

Lako je razumjeti da se definicija granice niza može formulirati na sljedeći način: to je određeni broj na koji se svi članovi niza beskonačno približavaju. Jednostavan primjer: a _x = 4x ​​+ 1. Tada će sam slijed izgledati ovako.

5, 9, 13, 17, 21 ... x ...

Dakle, ova sekvenca će se beskonačno povećavati i, prema tome, njezina granica jednaka je beskonačnosti kao x → should, a to treba napisati kao:

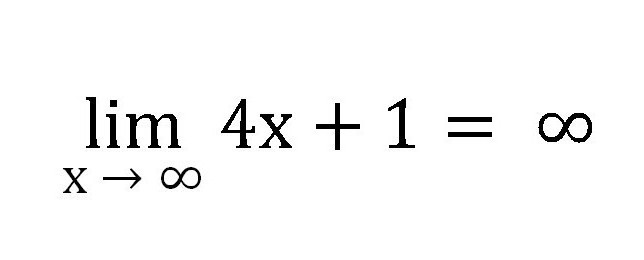
Ako uzmemo sličan slijed, ali x će težiti 1, dobit ćemo:

a _x = 4x ​​+ 1.

Niz brojeva bit će sljedeći: 1.4, 1.8, 4.6, 4.944 i tako dalje. Svaki put morate zamijeniti broj sve bliže jednom (0.1, 0.2, 0.9, 0.986). Iz ove serije jasno je da je granica funkcije pet.

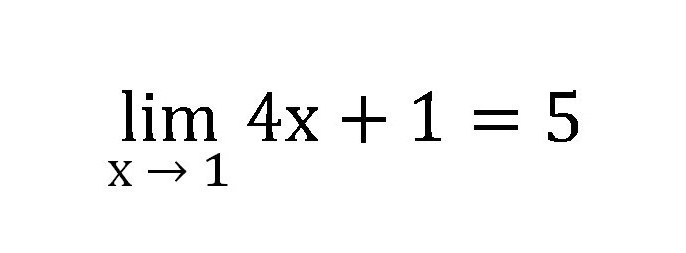
Iz ovoga se dijela treba sjetiti što je granica numeričkog niza, definicija i metoda rješavanja jednostavnih zadataka.

Opće označavanje granice sekvenci

Ispitujući granicu numeričkog niza, njegovu definiciju i primjere, možemo preći na složeniju temu. Apsolutno sve granice sekvenci mogu se formulirati s jednom formulom, koja se obično analizira u prvom semestru.

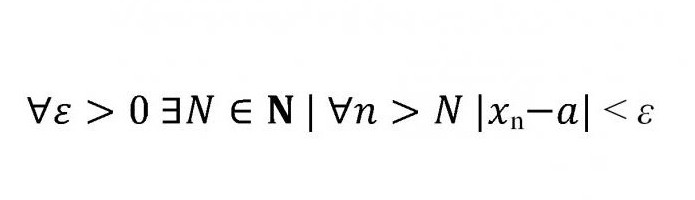
Što znači ovaj skup slova, modula i znakova nejednakosti?

Quant - kvantifikator univerzalnosti, zamjenjujući izraze “za sve”, “za sve”, itd.

∃ - kvantifikator postojanja, u ovom slučaju znači da postoji neka vrijednost N koja pripada skupu prirodni brojevi.

Dugi vertikalni štapić, slijedeći N, znači da je zadani skup N "takav da." U praksi, to može značiti "tako da", "tako da", itd.

Slijedi modul. Očito je da je modul udaljenost, koja po definiciji ne može biti negativna. Dakle, modul razlike je strogo manji od "epsilon".

Da bi se materijal konsolidirao, glasno pročitajte formulu.

Nesigurnost i određenost ograničenja

Metoda pronalaženja granice sekvenci, o kojoj smo već govorili, jednostavna je u upotrebi, ali u praksi nije toliko racionalna. Pokušajte pronaći granicu za takvu funkciju:

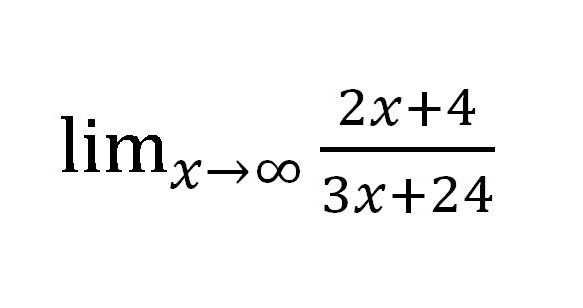
Ako zamjenimo različite vrijednosti "X" (svaki put se povećava: 10, 100, 1000, itd.), U brojniku dobivamo ∞, ali u nazivniku također ∞. Ispada prilično neobična frakcija: 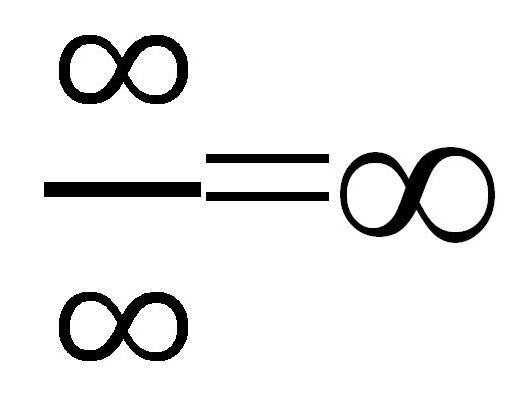Ali je li to stvarno? Izračunajte granicu numeričkog niza u ovom slučaju čini se prilično jednostavnim. Bilo bi moguće ostaviti sve kako jest, jer je odgovor spreman, a primljen je pod razumnim uvjetima, ali postoji drugi način posebno za takve slučajeve.

Za početak, najveću snagu nalazimo u brojniku jedne frakcije - ona je 1, budući da x može biti predstavljena kao x ¹ .

Sada nalazimo najveću snagu u nazivniku. Također 1.

Podijelili smo i brojnik i nazivnik u varijablu u najvišem stupnju. U ovom slučaju, frakcija je djeljiva s x ¹ .

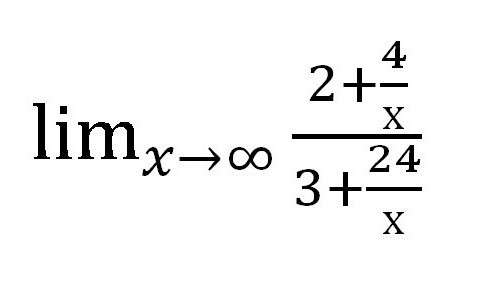
Zatim ćemo pronaći koju vrijednost dodaje svaki dodatak koji sadrži varijablu. U ovom slučaju, frakcija. Kao x → ∞, vrijednost svake od frakcija teži nuli. Pri izradi pisanog rada vrijedi izraditi takve fusnote:

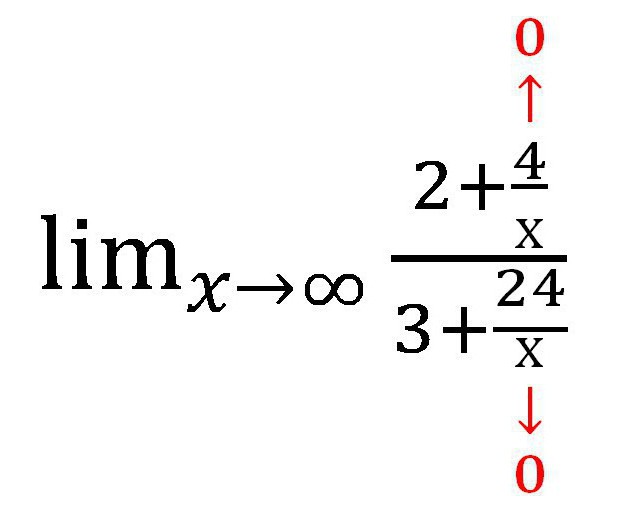
Dobiva se sljedeći izraz:

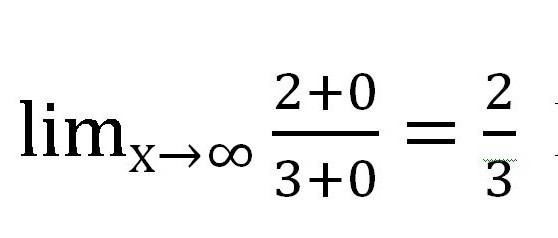
Naravno, frakcije koje sadrže x nisu postale nule! Ali njihova je vrijednost toliko mala da je potpuno dopušteno da se ne uzme u obzir pri izračunavanju. Zapravo, x u ovom slučaju nikada neće biti jednako 0. jer se nula ne može podijeliti.

Što je susjedstvo?

Pretpostavimo da profesor ima na raspolaganju složenu sekvencu, koja se, očito, daje ne manje složenom formulom. Profesor je pronašao odgovor, ali je li prikladan? Uostalom, svi su ljudi u krivu.

Auguste Cauchy je u svoje vrijeme smislio odličan način da dokaže granice sekvenci. Njegova metoda nazvana je upravljanje susjedstvom.

Pretpostavimo da postoji neka točka a, njezino susjedstvo u oba smjera na brojevnoj liniji je ε ("epsilon"). Budući da je zadnja varijabla udaljenost, njezina je vrijednost uvijek pozitivna.

Sada definiramo neki slijed x _n i pretpostavimo da je deseti izraz sekvence (x ₁₀ ) ulazi u susjedstvo. Kako napisati ovu činjenicu u matematičkom jeziku?

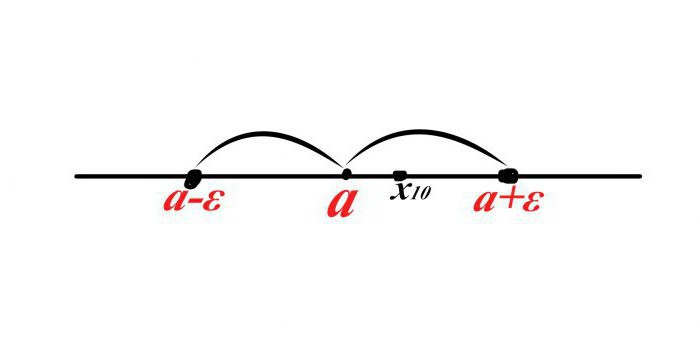
Pretpostavimo da je x ₁₀ desno od točke a, onda je udaljenost x ₁₀ –a <ε, međutim, ako postavite “X deseti” na lijevo od točke a, onda će udaljenost biti negativna, ali to je nemoguće, tada biste trebali dodati modul lijevom dijelu nejednakosti. | X ₁₀ –a | <ε.

Sada je vrijeme da u praksi pojasnimo tu formulu, koja je gore spomenuta. Određeni broj a s pravom se naziva krajnjom točkom slijeda ako je za bilo koje njezino ograničenje zadovoljena nejednakost ε> 0, a cijelo susjedstvo ima svoj prirodni broj N, tako da će svi članovi slijeda s značajnijim brojevima biti unutar slijeda | x _n - a | ,

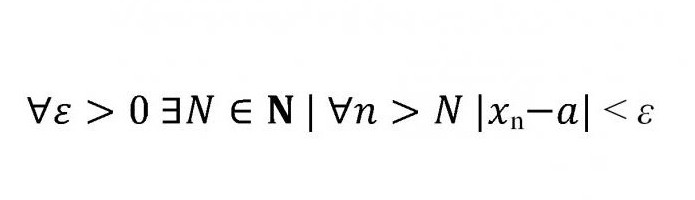
S takvim znanjem lako je provesti rješenje do granica niza, dokazati ili opovrgnuti spreman odgovor.

teorema

Teoreme ograničenja slijeda važna su komponenta teorije, bez koje je praksa nemoguća. Postoje samo četiri glavna teorema, sjetivši se da je, ponekad, moguće olakšati tijek rješenja ili dokaza:

1. Jedinstvenost ograničenja niza. Ograničenje za bilo koji slijed može biti samo jedno ili nije. Isti primjer s redom, koji može imati samo jedan kraj.
2. Ako niz brojeva ima ograničenje, onda je slijed tih brojeva ograničen.
3. Granica zbroja (razlika, proizvod) sekvenci jednaka je zbroju (razlika, proizvod) njihovih granica.
4. Granica kvocijenta od podjele dvaju sekvenci jednaka je kvocijentu granica ako i samo ako nazivnik ne nestaje.

Dokaz o sekvencama

Ponekad je potrebno riješiti inverzni problem, kako bi se dokazala zadana granica numeričkog niza. Razmotrite primjer.

Dokazati da je granica sekvence koju daje formula jednaka nuli.

U skladu s gore navedenim pravilom, za svaki slijed mora biti zadovoljena nejednakost | x _n - a | <ε. Zamijenite navedenu vrijednost i referentnu točku. Dobivamo:

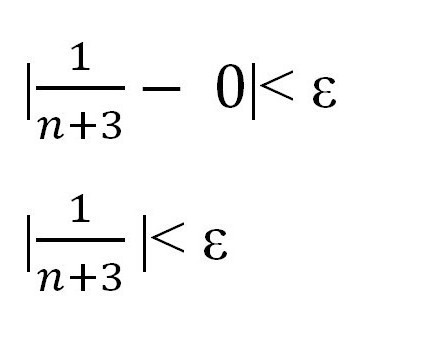
Izrazite n kroz "epsilon" kako biste pokazali postojanje određenog broja i dokazali postojanje graničnog niza.

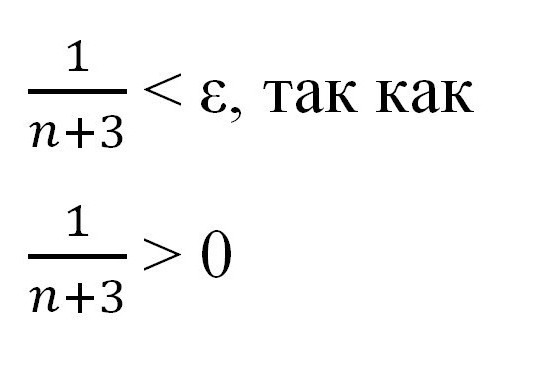
U ovoj fazi, važno je podsjetiti da su "epsilon" i "en" brojevi pozitivni i ne-nula. Sada možete nastaviti s daljnjim transformacijama koristeći znanje o nejednakostima dobivenim u srednjoj školi.

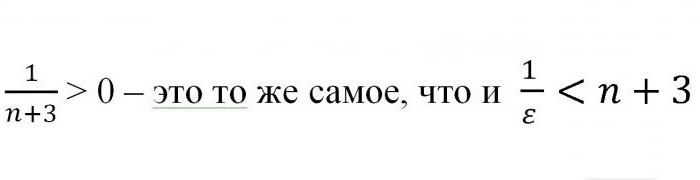
Otuda ispada da je n> –3 + 1 / ε. Budući da se valja sjetiti da govorimo o prirodnim brojevima, rezultat se može zaokružiti stavljanjem u uglate zagrade. Tako je dokazano da je za svaku vrijednost susjedstva "epsilon" točke a = 0 postojala takva vrijednost da početna nejednakost vrijedi. Iz toga možemo sa sigurnošću reći da je broj a granica zadanog slijeda. Što je trebalo dokazati.

S takvom prikladnom metodom, može se dokazati granica numeričkog niza, koliko god se na prvi pogled činio složenim. Glavna stvar - ne paničariti u očima posla.

Ili možda nije?

Postojanje graničnog niza u praksi je opcionalno. Lako možete pronaći takav niz brojeva koji stvarno nemaju kraja. Na primjer, ista bljeskalica x _n = (–1) ⁿ . očito je da slijed koji se sastoji od samo dva broja, ciklički ponavljajućih, ne može imati granicu.

Ista se povijest ponavlja sa sekvencama koje se sastoje od jednog broja, djelomičnog, koje tijekom računanja imaju nesigurnost bilo kojeg reda (0/0, ∞ / ∞, 0/0, itd.). Međutim, treba imati na umu da je došlo i do pogrešnog izračuna. Ponekad će granica sekvenci pomoći da ponovno provjerite vlastita rješenja.

Monotoni slijed

Iznad smo razmotrili nekoliko primjera sekvenci, metode za njihovo rješavanje, a sada ćemo pokušati uzeti specifičniji slučaj i nazvati ga “monotonim slijedom”.

Definicija: pošteno je nazvati bilo koji slijed koji se monotono povećava ako za njega vrijedi stroga nejednakost x _n <x _{n +1.} Također, svaka sekvenca se s pravom naziva monotonskim opadanjem ako za nju vrijedi nejednakost x _n > x _{n + 1.}

Uz ova dva uvjeta, postoje i slične slabe nejednakosti. Prema tome, x _n ≤ x _{n + 1} (slijed koji se ne smanjuje) i x _n ≥ x _{n + 1} (sekvenca koja se ne povećava).

Ali to je lakše shvatiti s primjerima.

Slijed dobiven formulom x _n = 2 + n tvori sljedeći niz brojeva: 4, 5, 6, itd. Ovo je monotono rastuća sekvenca.

A ako uzmemo x _n = 1 / n, dobivamo niz: 1/3, ¼, 1/5, itd. Ovo je monotono opadajući slijed.

Granica konvergentnog i ograničenog slijeda

Ograničeni slijed - slijed koji ima ograničenje. Konvergentni slijed je niz brojeva koji ima beskonačno malu granicu.

Prema tome, granica ograničenog slijeda je valjana ili kompleksni broj. Ne zaboravite da postoji samo jedna granica.

Granica konvergentnog slijeda je beskonačno mala količina (stvarna ili složena). Ako nacrtate dijagram sekvence, onda će se na određenoj točki činiti da se približava, težeći okrenuti se određenoj vrijednosti. Otuda ime - konvergentni slijed.

Monotono ograničenje

Granica za takav niz može ili ne mora biti. U početku je korisno razumjeti kada je to, od koje se može odgurnuti kada dokazuje odsutnost ograničenja.

Među monotonim sekvencama emitiraju se konvergirajuće i divergentne. Konvergiranje je slijed koji se formira iz skupa x i ima realno ili složeno ograničenje u skupu. Divergent - niz koji nema ograničenja u svom skupu (niti stvaran niti složen).

Osim toga, slijed konvergira ako njegova geometrijska slika konvergira gornju i donju granicu.

Granica konvergentne sekvence u mnogim slučajevima može biti jednaka nuli, budući da svaka beskonačno mala sekvenca ima poznatu granicu (nula).

Bez obzira na konvergirajuću sekvencu, svi su oni ograničeni, ali ne sve ograničene sekvence konvergiraju.

Zbroj, razlika, proizvod dvaju konvergentnih sekvenci također je konvergentna sekvenca. Međutim, kvocijent može biti i konvergentan ako je definiran!

Razne akcije s ograničenjima

Granice sekvenci su jednako značajne (u većini slučajeva) kao brojevi i brojevi: 1, 2, 15, 24, 362 itd. Ispostavilo se da se neke operacije mogu izvoditi s ograničenjima.

Prvo, kao i brojevi i brojevi, mogu se dodati i oduzeti granice bilo koje sekvence. Na temelju trećeg teorema o granicama nizova vrijedi sljedeća jednakost: granica zbroja nizova jednaka je zbroju njihovih granica.

Drugo, na temelju četvrtog teorema o granicama sekvenci, sljedeća jednakost je istinita: granica proizvoda n-tog broja sekvenci jednaka je produktu njihovih granica. Isto vrijedi i za podjelu: granica kvocijenta dviju sekvenci jednaka je kvocijentu njihovih granica, pod uvjetom da granica nije nula. Uostalom, ako je granica sekvenci jednaka nuli, tada dobivamo podjela na nulu, što je nemoguće.

Svojstva slijeda

Čini se da je granica numeričkog niza već detaljno analizirana, ali takvi izrazi kao što su "beskonačno mali" i "beskonačno veliki" brojevi spominju se više puta. Očito, ako postoji slijed 1 / x, gdje je x → ∞, onda je takva frakcija beskonačno mala, a ako je slijed jednak, ali granica teži nuli (x → 0), tada frakcija postaje beskonačno velika količina. Takve količine imaju svoje osobine. Svojstva granice niza koji imaju male ili velike vrijednosti su kako slijedi:

1. Zbroj bilo koje količine proizvoljno malih količina također će biti mala količina.
2. Zbroj bilo kojeg broja velikih količina bit će beskonačno velika količina.
3. Proizvod proizvoljno malih veličina beskonačno je mali.
4. Produkt bilo kojeg broja velikih brojeva je beskrajno velika vrijednost.
5. Ako izvorna sekvenca teži beskonačno velikom broju, tada će količina koja je suprotna njoj biti beskonačno mala i teži nuli.

U stvari, izračunavanje granice niza nije tako težak zadatak ako znate jednostavan algoritam. Ali granice sekvenci - tema koja zahtijeva maksimalnu pozornost i ustrajnost. Dakako, dovoljno je samo uhvatiti suštinu rješenja takvih izraza. Počevši od malih, s vremenom možete doseći velike vrhove.