Kako pronaći područje jednakokračnog trokuta?
Matematika je nevjerojatna znanost. Međutim, takva misao dolazi samo onda kada je shvatite. Da biste to postigli, trebate riješiti probleme i primjere, nacrtati dijagrame i crteže, dokazati teoreme.
Put do razumijevanja geometrije je kroz rješavanje problema. Izvrstan primjer je zadatak u kojem morate pronaći područje jednakokračnog trokuta.
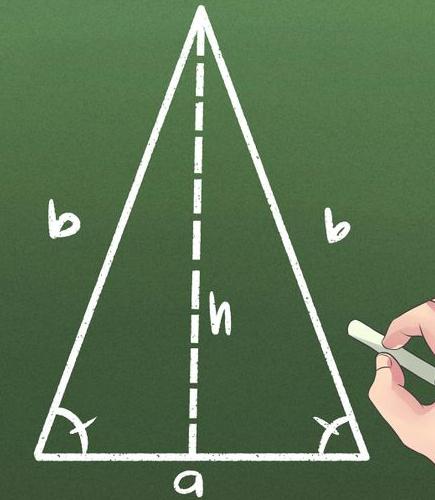
Što je jednakokračan trokut i kako se razlikuje od drugih?
Kako se ne bi bojali termina "visina", "područje", "baza", "jednakokračan trokut" i drugi, morat ćete početi od teorijske osnove.
Prvo o trokutu. To je ravna figura, koja se formira iz tri točke - vrhovi, pak, povezani segmentima. Ako su dvije od njih jednake jedna drugoj, tada trokut postaje jednakokračan. Te su strane nazvane strane, a ostalo je postalo temelj.
Postoji poseban slučaj jednakostraničnog trokuta - jednakostraničan, kada je treća strana jednaka dvije strane.
Svojstva oblika
Dokazuju se kao vjerni asistenti u rješavanju problema koji zahtijevaju pronalaženje područja jednakokračnog trokuta. Stoga je potrebno znati i upamtiti ih.
- Prvi od njih: kutovi jednakostraničnog trokuta, čija je jedna strana baza, uvijek su međusobno jednaki.
- Imovina o dodatnim konstrukcijama je također važna. Visine neparne strane, medijana i simetrala se podudaraju.
- Ovi segmenti, izvučeni iz uglova u podnožju trokuta, parno su jednaki. To prečesto olakšava pronalaženje rješenja.
- Dva jednaka kuta uvijek su manje od 90º.
- I na kraju: upisani i ograničeni krugovi konstruirani su tako da njihovi centri leže na visini baze trokuta, što znači medijana i simetrala.

Kako prepoznati jednakokračan trokut u problemu?
Ako se pri rješavanju zadatka postavlja pitanje kako pronaći područje jednakostraničnog trokuta, onda prvo morate shvatiti da pripada toj skupini. A to će pomoći određenim znakovima.
- Jednako dva kuta ili dvije strane trokuta.
- Simetrala je također medijana.
- Visina trokuta je medijana ili simetrala.
- Jednaka je dvjema visinama, sredinama ili simetralima figure.
Oznake količina koje su usvojene u razmatranim formulama
Kako bi se pojednostavilo kako pronaći područje jednakostraničnog trokuta pomoću formula, uvedena je zamjena njezinih elemenata slovima.
| Slovo u formuli | ime |
| i | bok |
| u | duljina baze |
| n | visine do baze |
| угол при основании osnovni kut | |
| величина угла, лежащего между боковыми сторонами kut između strana | |
| zajednička oznaka | područje |
Upozorenje! Važno je ne brkati "a" s "A" i "b" s "B". To su različite količine.
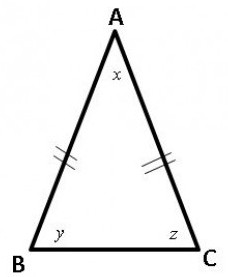
Formule koje se mogu koristiti u različitim zadacima
Duljine stranica su poznate i potrebno je pronaći područje jednakokračnog trokuta.
U tom slučaju morate kvadrirati obje vrijednosti. Broj koji je došao iz promjene strane, pomnožite sa 4 i oduzmite drugi od njega. Izvadite iz dobivene razlike kvadratni korijen. Duljina baze podijeljena s 4. Dva broja se množe. Ako te radnje napišete slovima, dobivate sljedeću formulu:
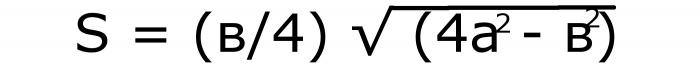
Neka se bilježi pod brojem 1.
Nađite po vrijednostima strane područje jednakostraničnog trokuta. Formula koja se nekome može činiti jednostavnijom od prve.
Prvi korak je pronaći pola baze. Zatim pronađite zbroj i razliku tog broja sa stranom. Pomnožite posljednje dvije vrijednosti i izvadite kvadratni korijen. Posljednji korak je umnožavanje svega na pola baze. Ravnost pisma će izgledati ovako:
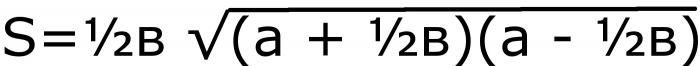
To je formula broj 2.
Način pronalaženja područja jednakokračnog trokuta, ako su baza i visina poznati.
Jedna od najkraćih formula. Potrebno je pomnožiti obje vrijednosti podataka i podijeliti ih na 2. Evo kako će biti napisano:

Broj ove formule je 3.
U zadatku su poznate strane trokuta i kut između baze i strane.
Ovdje, da bi se saznalo koje je područje jednakokračnog trokuta jednako, formula će se sastojati od nekoliko čimbenika. Prva od njih je vrijednost sinusa kuta. Drugi je jednak proizvodu strane prema bazi. Treći je dio ½. Opća matematička notacija:

Redni broj formule je 4.
U zadatku su dane: strana jednakokračnog trokuta i kut koji leži između njegovih strana.
Kao iu prethodnom slučaju, područje se nalazi na tri faktora. Prvi je jednak sinusu kuta navedenog u stanju. Drugi je kvadrat sa strane. I potonji je jednak polovici jedinice. Kao rezultat, formula je napisana kao:
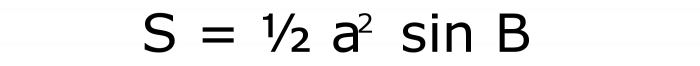
Broj joj je 5.
Formula koja vam omogućuje da pronađete područje jednakokračnog trokuta, ako znate njegovu bazu i kut nasuprot njemu.
Prvo morate izračunati tangens od pola poznatog kuta. Pomnožite dobiveni broj s 4. Trgajte duljinu stranice, koja se zatim dijeli s prethodnom vrijednošću. Tako dobivamo sljedeću formulu:

Broj posljednje formule je 6.
Primjeri zadataka
Prvi zadatak: poznato je da je osnova jednakostraničnog trokuta 10 cm, a visina mu je 5 cm.
Da bi se to riješilo, logično je odabrati formulu broj 3. U njoj je sve poznato. Zamijenite brojeve i brojite. Ispada da je područje 10 * 5 / 2. To je, 25 cm 2 .

Drugi zadatak: u jednakokračnom trokutu, dani su bočni i donji dio, koji su 5 i 8 cm.
Prvi način. Prema formuli broj 1. Kada se kvadrira baza, dobiva se broj 64, a četverostruki kvadrat na strani je 100. Nakon oduzimanja od drugog, prvi će rezultirati s 36. Korijen je savršeno izvučen iz njega, što je 6. Baza podijeljena sa 4 je 2. Konačna vrijednost se definira kao proizvod 2. i 6, odnosno 12. To je odgovor: tražena površina je 12 cm 2 .
Drugi način. Prema formuli broj 2. Polovica baze jednaka je 4. Zbroj strane i pronađenog broja daje 9, a razlika je 1. Nakon množenja, dobivamo 9. Uklanjanje kvadratnog korijena daje 3. I posljednju akciju, množenjem 3 sa 4, što daje isti 12 cm2.

Savjet: kako voljeti matematiku
Rješavajući probleme u geometriji i određujući kako pronaći područje jednakostraničnog trokuta, možete dobiti neprocjenjivo iskustvo. Što se više različitih zadataka obavlja, lakše je pronaći odgovor u novoj situaciji. Stoga je redovito i samostalno obavljanje svih zadataka put do uspješnog učenja materijala.