Kako pronaći stranu trokuta - pomoći učeniku

Postoji nekoliko načina za rješavanje tog geometrijskog problema. Oni su opisani u članku.

Sa stranama i uglovima

Dakle, prvi način pronalaženja stranica trokuta je na nekoliko strana, a kut između njih (i slično s uglovima i jednom susjednom stranom). Ova metoda je prikladna za srednju školu jer koristi koncepte kao što su sinus, kosinus, kvadratni broj i korijen. Dakle, kako pronaći stranu trokuta, koja je proizvoljna? Za početak, nacrtajte ovaj lik. Nazovimo sada elemente naše figure. Stranke će biti a, b i c. Kut, smješten nasuprot a, imat ćemo alfa, nasuprot b - beta, nasuprot c - gama. 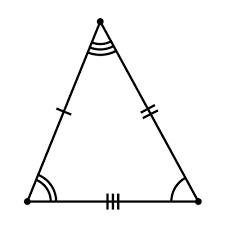Da biste pronašli stranu, recimo, a, morate izračunati kvadratni korijen od zbroja kvadrata b, c i od njega oduzimamo dvostruki proizvod kosinusa kuta a na stranama b i c. To jest, da bismo olakšali oblik formule i objasnili kako pronaći stranu trokuta proizvoljnog oblika, možemo napisati sljedeće: a = (b * b + c * c-2 * b * c * cos "alfa") ^ (1 / 2). Budite oprezni, jer ako je kut nasuprot željenoj strani tup, onda će kosinus imati negativnu vrijednost. Još jedna formula za pronalaženje strana trokuta je na dva ugla i strane. Odmah dajemo formulu-jednakost, jer je za razumijevanje vizualnog oblika jednostavnije od dugog slikarstva. Još uvijek moramo pronaći stranu a. Zatim, na temelju zapisa, dobivamo sljedeće: a = (b * sin "alpha") / sin "beta" = (b * sin "alfa") / sin ("alfa" + "gama") = (b * sin ( "beta" + "gama")) / sin "beta". To je lukav način pronalaženja nepoznate strane proizvoljnog trokuta.

Jednolikog trokuta

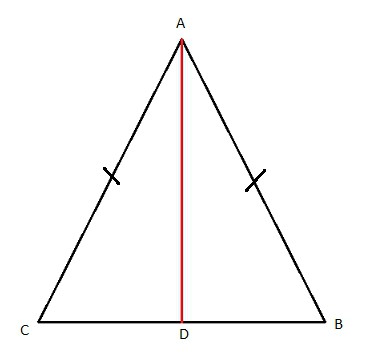
Što je jednakokračan trokut? Sam po sebi ima dvije identične strane i tzv. Bazu. Dvostruke strane označene su slovom a, baza - b. Dakle, budući da trokut ima dva "kuka" iste veličine, onda će i kutovi na "temeljima" također biti isti. Nazovimo ih alfa. Da biste odgovorili kako pronaći stranu jednakokračnog trokuta, trebate unijeti drugu vrijednost - kut između jednakih "kukova".
Budući da se nalazi nasuprot b, najbolje je nazvati "beta". Ovdje, kada tražite nepoznate strane, možete koristiti nekoliko formula. Da vidimo koje. Prve dvije su one po kojima možete izračunati duljinu strane baze jednakokračnog trokuta. Temelji se na učenikovom znanju o sinusima i kosinusima. 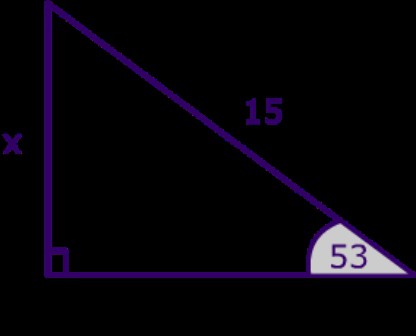Dakle, naši izračuni izgledaju ovako: b = 2 * a * sin ("beta" / 2) = a * (2-2 * cos "beta") ^ (1/2) ili b = 2 * a * cos „a”. Jednostavno i jednostavno. Pogotovo ako "dobijete ruku" i vježbate. Sada možemo pogledati kako izračunati duljinu jednakih strana. I ovdje postoje dvije mogućnosti, malo su složenije od prethodnih. Izgledaju glomazno, ali ne biste trebali biti uplašeni. Kako pronaći "bokove"? Imat ćemo sljedeće formule: a = b / (2 * sin ("beta" / 2)) = b / (2-2 * cos "beta") ^ (1/2) ili a = b / (2 / cos "alfa"). Koji zapis trebam koristiti? Sve ovisi o zadatku i uvjetima. Naravno, možete provjeriti izračune za sve formule, ako imate apsolutno sve podatke. Sada možemo krenuti dalje.

Pravokutni trokut

Vjerojatno svaki učenik koji je tek počeo proučavati geometriju zna što pravokutni trokut. Na prvi pogled ta brojka nije ništa posebno, složeno i nerazumljivo. Ali kada se problemi izgube oko jedne ili druge strane tog geometrijskog objekta, počinju problemi. Stvar je u tome da pitanje: "Kako pronaći stranu pravog trokuta?" - utječe ne samo na pojmove sinus i kosinus, već i na tangente kutova. Dakle, kalkulacije postaju mnogo složenije i više. Dakle, najprije ćemo označiti dvije noge nacrtanog pravokutnog trokuta pomoću a i b. Kutovi koji leže nasuprot tim stranama, kao što je to ranije bilo uobičajeno, nazivaju se alfa i beta. Naša hipotenuza će biti strana c. Kut koji leži protiv njega nećemo trebati - bit će ravan. Postoji nekoliko varijanti izračuna. Prvi se zove klasik. Za nogu a, formule izgledaju kao: a = c * cos "beta" = c * sin "alpha" = b * tg "alfa".
Na sličan način nalazimo stranu b: b = c * cos "alpha" = c * sin "beta" = a * tg "beta". Tada se naša hipotenuza nalazi s: c = a / sin "alpha" = a / cos "beta" ili c = b / cos "alfa" = b / sin "beta". Druga, jednostavnija i poznata metoda pronalaženja strana pravokutnog trokuta je prema Pitagoreanskom teoremu. Kaže: zbroj kvadrata dviju nogu jednak je kvadratu hipotenuze. Dakle, imat ćemo sljedeće: a = (c * cb * b) ^ (1/2), b = (c * ca * a) ^ (1/2), c = (b * b + a * a) ^ (1/2). Ovdje je jednostavan i jasan odgovor na pitanje kako pronaći stranu trokuta. Nemojte se bojati velikih izračuna.

rezultati

Dakle, danas smo shvatili kako pronaći stranu trokuta i naučili puno novih formula. Da bi ih bolje zapamtili, zapišite ih na neki list papira, na kojem će kasnije biti lakše naučiti sve napamet. Nemojte se bojati "zastrašujućih" brojeva i velikih izračuna. Sve je lakše nego što se čini.