Logaritmi: pravila, osnovna svojstva i formule

Logaritmi i pravila djelovanja s njima su prilično prostrani i jednostavni. Stoga, da biste razumjeli ovu temu, nećete biti teško. Nakon što naučite sva pravila prirodnih logaritama, svaki problem će se riješiti samostalno. Prvo poznavanje ove teme može izgledati dosadno i besmisleno, ali uz pomoć logaritama riješeni su mnogi problemi matematičara 16. stoljeća. "O čemu se radi?" - pomislili ste. Pročitajte članak do kraja i otkrijte da ovaj odjeljak "Czarina of Sciences" može biti zanimljiv ne samo matematičarima, znanstvenicima egzaktnih znanosti, nego i običnim srednjoškolcima.

Definicija logaritma

Počnimo s definicijom logaritma. Kao što u mnogim udžbenicima piše: logaritam broja b na temelju a (log _a b) je određeni broj c za koji ta jednakost vrijedi: b = a ^c . To jest, jednostavno rečeno, logaritam je određeni stupanj u kojem gradimo bazu da bismo dobili određeni broj. Ali važno je zapamtiti da logaritam obrasca log _a b ima smisla samo kada: a> 0; a je broj različit od 1; b> 0, stoga zaključujemo da se logaritam može naći samo za pozitivne brojeve.

Klasifikacija logaritama po bazi

Logaritmi mogu biti bilo koji pozitivni broj u bazi. No postoje i dvije vrste: prirodni i decimalni logaritmi.

• Prirodni logaritam - logaritam s bazom e (e je Eulerov broj, brojčano približno jednak 2.7, iracionalni broj koji je uveden za eksponencijalnu funkciju y = e ^x ) označen je kao ln a = log _e a;
• Decimalni logaritam je logaritam s bazom 10, tj. Log ₁₀ a = lg a.

Osnovna pravila logaritama

Prvo se morate upoznati s osnovnim logaritamskim identitetom: ^{log _a b} = b, a zatim slijedite ova dva osnovna pravila:

• log _a 1 = 0 - budući da je bilo koji broj u nultom stupnju 1;
• log _a a = 1.

Zahvaljujući otkriću logaritma, nije nam teško riješiti apsolutno bilo kakvu eksponencijalnu jednadžbu, čiji se odgovor ne može izraziti prirodnim brojevima, već samo iracionalnim. Na primjer: 5 ^x = 9, x = log ₅ 9 (budući da za ovu jednadžbu nema prirodnog x).

Radnje s logaritmima

• log _a (x · y) = prijavite x + log _a y - da biste pronašli logaritam proizvoda, morate dodati logaritme faktora. Imajte na umu da su baze logaritama iste. Ako to napišemo obrnutim redoslijedom, dobivamo pravilo dodavanja logaritama.
• log _a xy = log _a x - log _a y - kako bi pronašli logaritam pojedinog, potrebno je pronaći razliku između logaritama dividende i djelitelja. Imajte na umu: logaritmi imaju istu bazu. Kod pisanja obrnutim redoslijedom dobivamo pravilo oduzimanja logaritama.

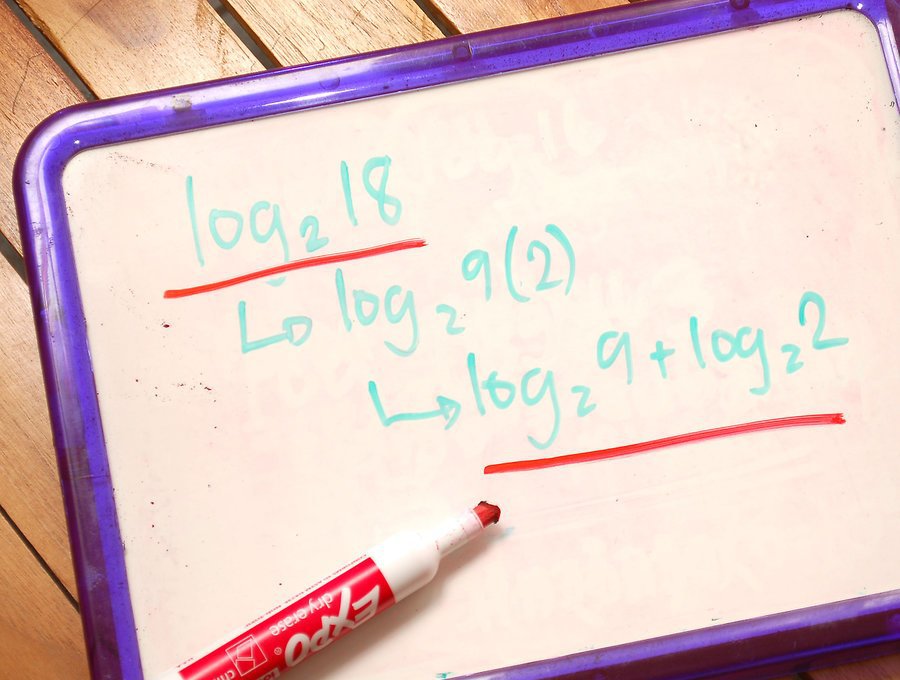
• log _{a ^k} x ^p = (p / k) * log _a x - dakle, ako postoje argumenti i osnovice logaritma, onda ih možemo uzeti iz logaritamskog znaka.
• log _a x = log _{a ^c} x ^c je poseban slučaj prethodnog pravila, kada su eksponenti jednaki, mogu se smanjiti.
• log _a x = (log _b x) (log _b a) je tzv. tranzicijski modul, postupak pretvaranja logaritma u drugu bazu.
• log _a x = 1 / log _x a je poseban slučaj prijelaza, promjena mjesta baze i zadanog broja. Cijeli izraz, figurativno govoreći, preokreće se, a logaritam s novom bazom pojavljuje se u nazivniku.

Povijest logaritama

U 16. stoljeću postalo je neophodno provesti mnoge približne izračune za rješavanje praktičnih problema, uglavnom u astronomiji (na primjer, određivanje položaja Sunca ili zvijezda broda).

Ta je potreba brzo rasla, a znatne poteškoće stvorile su množenje i podjelu višeslojnih brojeva. I matematički matematičar Napier je odlučio zamijeniti radno intenzivno umnožavanje običnim dodatkom za trigonometrijske izračune, uspoređujući neke progresije za to. Tada se podjela, na sličan način, zamjenjuje jednostavnijim i pouzdanijim postupkom - oduzimanjem, a da bi se izdvojio korijen n-tog stupnja, potrebno je podijeliti logaritam radikala na n. Rješenje tako teškog zadatka u matematici jasno je odražavalo Naperove ciljeve u znanosti. Evo kako je o tome pisao na početku svoje knjige Rabdologiya:

Uvijek sam nastojala, što se tiče mojih moći i sposobnosti, osloboditi ljude od poteškoća i dosade računanja, što mučnina obično zastrašuje mnoge ljude od učenja matematike.

Naziv logaritam je predložio sam Napier, dobiven je kombiniranjem grčkih riječi, što je u kombinaciji značilo "broj odnosa".

Baza logaritma uvela je Spadel. Posudio je Eulera iz teorije stupnjeva i prešao u teoriju logaritama. Koncept logaritmizma postao je slavan zahvaljujući Koppu u 19. stoljeću. Korištenje prirodnih i decimalnih logaritama, kao i njihovih oznaka, pojavilo se zahvaljujući Cauchyju.

Godine 1614. John Napier je na latinskom objavio esej "Opis nevjerojatne tablice logaritama". Tu je kratak opis logaritama, pravila i njihovih svojstava. Stoga je termin "logaritam" uspostavljen u egzaktnim znanostima.

Operacija logaritma i prvi spomen toga pojavili su se zahvaljujući Wallisu i Johannu Bernoulliju, a konačno ju je utemeljio Euler u XVIII.

To je Eulerova zasluga u proširenju logaritamske funkcije oblika y = log _a x na kompleksnu domenu. U prvoj polovici XVIII. Stoljeća objavljena je njegova knjiga "Uvod u analizu beskonačnosti", u kojoj su se pojavile suvremene definicije eksponencijalnih i logaritamskih funkcija.

Logaritamska funkcija

(имеет смысл, только если: а > 0, а ≠ 1). Funkcija oblika y = log _a x (ima smisla samo ako: a> 0 i ≠ 1).

• Logaritamska funkcija određena je skupom svih pozitivnih brojeva, budući da zapisni zapis _a x postoji samo pod uvjetom - x> 0 ;.
• Ova funkcija može uzeti apsolutno sve vrijednosti iz skupa R (realnih brojeva). Budući da svaki stvarni broj b ima pozitivan x kako bi zadovoljio jednakost log _a x = b, to jest, ova jednadžba ima korijen - x = a ^b (slijedi iz činjenice da log _a a ^b = b).
• Funkcija se povećava na intervalu a> 0 i smanjuje na intervalu 0 <a <1.
• Ako je a> 0, tada funkcija dobiva pozitivne vrijednosti za x> 1.

Treba imati na umu da svaki grafikon logaritamske funkcije y = log _i x ima jednu stacionarnu točku (1; 0), budući da je log _i 1 = 0. To se jasno vidi na ilustraciji donjeg grafikona.

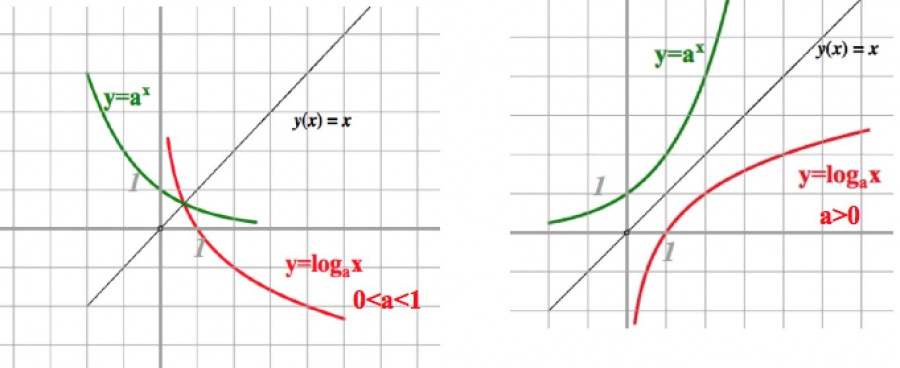
Kao što vidimo na slikama, funkcija nema ravnost ili neobičnost, nema najvećih ili najmanjih vrijednosti, nije ograničena odozgo ili odozdo.

Logaritamska funkcija y = log _a x i eksponencijalna funkcija y = a ^x , gdje su (a> 0 i) 1) međusobno inverzni. To se može vidjeti na slici njihovih grafova.

Rješavanje problema s logaritmima

Obično rješenje problema koji sadrži logaritme temelji se na pretvaranju u standardni oblik ili je usmjereno na pojednostavljenje izraza pod znakom logaritma. Ili je potrebno prevesti uobičajene prirodne brojeve u logaritme s potrebnom osnovom, kako bi se provele daljnje operacije kako bi se pojednostavio izraz.

Postoje neke suptilnosti koje se ne smiju zaboraviti:

• Pri rješavanju nejednakosti, kada oba dijela stoje pod logaritmima prema pravilu s jednom bazom, nemojte žuriti “odbaciti” logaritamski znak. Zapamtite intervale monotonije logaritamske funkcije. Budući da je baza veća od 1 (slučaj kada se funkcija povećava) - znak nejednakosti ostaje nepromijenjen, ali kada je baza veća od 0 i manja od 1 (slučaj kada funkcija opada) - znak nejednakosti mijenja se u suprotno;
• _а х = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. Ne zaboravite definiciju logaritma: log _i x = b, a> 0, ≠ 1 i x> 0, kako ne biste izgubili korijene zbog neregistriranog raspona valjanih vrijednosti. TLD (dopušteni raspon vrijednosti) postoji za gotovo sve složene funkcije.

Pri rješavanju logaritamskih jednadžbi preporučuje se korištenje ekvivalentnih transformacija. Također, morate biti oprezni i uzeti u obzir moguće transformacije koje mogu dovesti do gubitka nekih korijena.

To su uobičajene, ali velike pogreške koje su se mnogi susreli u potrazi za pravim odgovorom za zadatak. Ne postoji toliko mnogo pravila za rješavanje logaritama, tako da je ova tema jednostavnija od drugih i kasnijih, ali treba dobro razumjeti.

zaključak

Ova tema na prvi pogled može se činiti komplicirana i glomazna, ali, istražujući je sve dublje i dublje, počinjete shvaćati da se tema upravo završava, a poteškoće ne uzrokuju ništa. Pregledali smo sva svojstva, pravila i čak pogreške vezane uz temu logaritama. Uspjesi u učenju!