Poincareova pretpostavka: povijest problema, dokaz, značenje

U školi svatko poznaje pojmove teorema i hipoteze. U pravilu, u životu utječu najjednostavniji i naj primitivniji zakoni, dok matematičari prave vrlo složene pretpostavke i postavljaju zanimljive probleme. Nisu uvijek sami uspjeli pronaći rješenja i dokaze, au nekim slučajevima i njihovi sljedbenici i pravedni kolege već se godinama bore.

Institut Clay je 2000. sastavio popis od 7 takozvanih Milenijskih izazova po analogiji s popisom hipoteza iz 1900. godine. Gotovo sve ove zadaće sada su riješene, samo je jedna od njih migrirala na ažuriranu verziju. Sada je popis problema sljedeći:

• Hodgeova pretpostavka;
• jednakost klasa P i NP;
• Poincareova pretpostavka;
• Yang-Millsova teorija;
• Riemannova hipoteza;
• postojanje i glatkoća rješavanja Navier-Stokesovih jednadžbi;
• Nagađanje Birch-Swinnerton-Dyer.

Svi oni pripadaju različitim disciplinama unutar matematike i važni su. Primjerice, Navier-Stokesove jednadžbe odnose se na hidrodinamiku, ali u praksi mogu opisati ponašanje tvari u zemaljskoj magmi ili biti korisne u predviđanju vremena. Ali svi ti problemi još uvijek traže svoj dokaz ili poricanje. Osim jednog.

Poincarev teorem

Teško je jednostavnim riječima objasniti u čemu je problem, ali možete pokušati. Zamislite kuglu, na primjer, mjehurić. Sve točke njezine površine jednako su udaljene od središta, koje mu ne pripadaju. Ali ovo je dvodimenzionalno tijelo, a hipoteza govori o trodimenzionalnom. Već je nemoguće zamisliti, ali imamo teoretsku matematiku. U ovom slučaju, naravno, sve točke ovog tijela također će biti uklonjene iz centra.

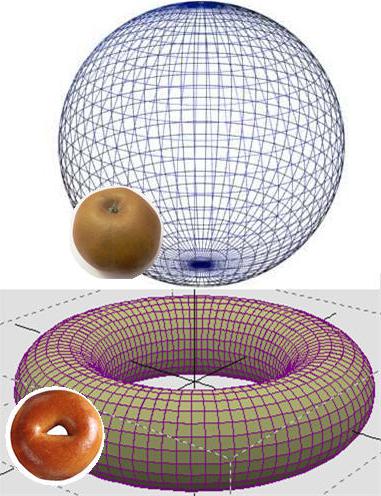
Ovaj se problem odnosi na topologiju - znanost o svojstvima geometrijskih oblika. I jedan od osnovnih pojmova u njemu je homeomorfizam, to jest visok stupanj sličnosti. Na primjer, možete zamisliti loptu i torus. Jedna se figura ne može dobiti iz druge, izbjegavajući pukotine, ali se konus, kocka ili cilindar iz prvog mogu dobiti vrlo lako. Ovdje je Poincareova hipoteza i tim metamorfozama posvećena je samo s jednom razlikom - govorimo o višedimenzionalnom prostoru i tijelima.

Povijest

Francuski matematičar Henri Poincare studirao je razna područja znanosti. O njegovim postignućima može se reći, na primjer, činjenica da je on neovisno o Albertu Einsteinu iznio glavne odredbe posebna teorija relativnosti. Godine 1904. postavio je problem dokazivanja da je bilo koje trodimenzionalno tijelo, koje posjeduje određena svojstva kugle, upravo do deformacije. Kasnije je proširena i generalizirana, te je postala poseban slučaj Thurstonove hipoteze formulirane 1982. godine.

formuliranje

Poincaré je u početku ostavio takvu tvrdnju: svako jednostavno povezano kompaktno trodimenzionalno mnoštvo bez granice je homeomorfno trodimenzionalnoj sferi. Kasnije je proširena i generalizirana. Pa ipak, dugo vremena to je bio izvorni zadatak koji je izazvao najviše problema, a riješen je samo 100 godina nakon njegova pojavljivanja.

Tumačenje i značenje

To je homeomorfizam, o čemu smo već raspravljali. Sada je vrijedno govoriti o kompaktnosti i singularnosti. Prvo znači samo da sorta ima ograničene veličine, ne može se neprekidno i beskonačno rastezati.

Što se tiče jedinstvenosti, možete pokušati dati jednostavan primjer. Dvodimenzionalna sfera - jabuka - ima jedno zanimljivo svojstvo. Ako uzmete uobičajenu zatvorenu gumu i pričvrstite je na površinu, tada se glatka deformacija može smanjiti na jednu točku. To je svojstvo jedinstvenosti, ali da ga predstavimo u odnosu na trodimenzionalni prostor prilično teško.

Jednostavno govoreći, problematično je bilo dokazati da je singularnost jedinstveno svojstvo za sferu. I ako se, relativno govoreći, iskustvo s gumenom trakom završi s takvim rezultatom, tijelo mu je homeomorfno. Što se tiče primjene te teorije u životu, Poincare je vjerovao da je svemir u određenom smislu trodimenzionalna sfera.

Dokaz

Nemojte misliti da je od desetaka matematičara koji su radili širom svijeta, nitko nije napredovao jednu jotu, rješavajući ovaj problem. Naprotiv, došlo je do napretka i na kraju je dovelo do rezultata. Poincaré sam nije imao vremena dovršiti posao, ali njegovo je istraživanje ozbiljno proširilo čitavu topologiju.

Tridesetih godina prošlog stoljeća vraćena je zainteresiranost za hipotezu. Prije svega, tekst je proširen na "n-dimenzionalni prostor", a zatim je američki Whitehead izvijestio o uspješnim dokazima, koji su ga kasnije napustili. U 60-70-ima, dva matematičara odjednom - Smale i Stallings - gotovo istodobno, ali na različite načine razvijaju rješenje za sve n veće od 4.

Godine 1982., i za 4, pronađeni su dokazi, preostale su samo 3. U istoj godini Thurston je formulirao hipotezu o geometrizaciji, a Poincaréova teorija postala je njezin poseban slučaj.

Tada je rad donekle zastao - Amerikanac Richard Hamilton predložio je korištenje Ricci tečenja u rješenju, ali je naišao na poteškoće i nije dovršio istraživanje.

Već 20 godina hipoteza Poincaréa kao da je zaboravljena. Godine 2002. ruski matematičar Grigorij Perelman predstavio je rješenje općenito, šest mjeseci kasnije donoseći neke dodatke. Kasnije su te dokaze testirali i doveli "sjaj" američkih i kineskih znanstvenika. Činilo se da je i sam Perelman izgubio sve zanimanje za problem, iako je riješio općenitiji problem geometrizacije, za što je Poincaréova pretpostavka samo poseban slučaj.

Priznavanje i vrednovanje

Naravno, to je odmah postalo senzacija, jer se rješenje jednog od Milenijskih problema jednostavno nije moglo zanemariti. Još više iznenađuje činjenica da je Gregory Perelman odbio sve nagrade i nagrade, rekavši da već ima divan život. U umovima običnih ljudi odmah je postao primjer tog polu-ludog genija koji je zainteresiran samo za znanost.

Sve je to izazvalo mnogo diskusija u tisku i medijima, da je popularnost matematičara postala njegova. U ljeto 2014. postojale su informacije da je Perelman otišao na posao u Švedsku, ali se ispostavilo da je to samo glasina, još uvijek živi skromno u St. Petersburgu i jedva komunicira s bilo kime. Među nagradama koje su mu dodijeljene nisu bile samo nagrade Instituta Clay, nego i prestižna Fields medalja, ali on je sve odbio. Međutim, Hamilton, koji je, prema Perelmanovim procjenama, dao manje važan doprinos dokazu, također nije zaboravljen. U 2009. i 2011. godini osvojio je i prestižne nagrade i priznanja.

Kulturna refleksija

Unatoč činjenici da za obične građane i izjava i rješenje ovog problema nemaju puno smisla, dokazi su postali poznati vrlo brzo. Godine 2008., japanski redatelj Masahito Kasuga snimio je dokumentarnim filmom "Očaravanje hipoteze Poincaréa", koji je tom prilikom posvećen svojim 100-godišnjim pokušajima da riješi taj problem.

Mnogi matematičari uključeni u ovaj problem sudjelovali su u pucnjavi, ali glavni lik, Grigorij Perelman, to nije želio. Više ili manje njegovih bliskih prijatelja također su sudjelovali u pucnjavi. Dokumentarni film, koji se pojavio na ekranima u svjetlu javne rezonancije o odbijanju znanstvenika da prihvati nagradu, osvojio je slavu u određenim krugovima i dobio nekoliko nagrada. Što se tiče masovna kultura, obični ljudi se još uvijek pitaju koje argumente vodi Petersburgski matematičar, odbijajući uzeti novac kad ga može dati, na primjer, u dobrotvorne svrhe.