Rotacijsko kretanje tijela. Zakon rotacijskog gibanja
Ovaj članak opisuje važan dio fizike - "Kinematika i dinamika rotacijskog gibanja".
Osnovni pojmovi kinematike rotacijskog gibanja
Rotacijsko gibanje materijalna točka oko fiksne osi naziva se takav pokret, čija je putanja kružnica smještena u ravnini okomitoj na os, a njeno središte leži na osi rotacije.
Rotacijsko gibanje čvrstog tijela je gibanje u kojem se sve točke tijela kreću duž koncentričnih krugova (čiji centri leže na istoj osi) u skladu s pravilom rotacijskog gibanja materijalne točke.
Neka proizvoljno kruto tijelo T rotira oko O-osi, koja je okomita na ravninu slike. Na tom tijelu odaberite točku M. Tijekom rotacije ova točka će opisati kružnicu s radijusom r oko osi O.
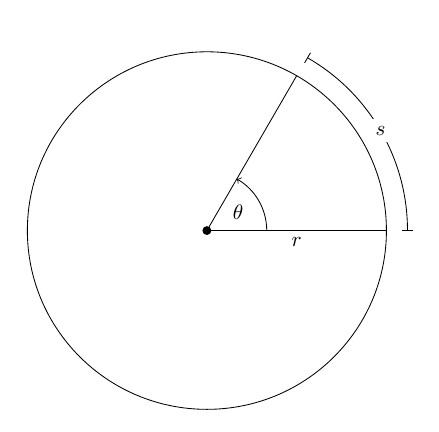
Nakon nekog vremena, polumjer će rotirati u odnosu na početni položaj za kut Δ.
Smjer desnog vijka (u smjeru kazaljke na satu) uzima se kao pozitivan smjer vrtnje. Promjena kuta rotacije s vremenom naziva se jednadžba rotacijskog gibanja krutine:
φ = φ (t).
Ako se φ mjeri u radijanima (1 rad je kut koji odgovara luku s duljinom jednakom njegovom radijusu), duljina luka kružnice ΔS, koju će materijalna točka M proći u vremenu Δt, jednaka je:
ΔS = Δφr.
Glavni elementi kinematike ravnomjernog rotacijskog gibanja
Mjera kretanja materijalne točke u kratkom vremenu dt je elementarni rotacijski vektor dφ .
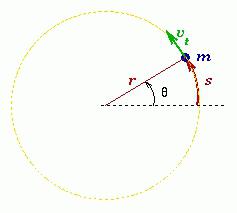
Kutna brzina Materijalna točka ili tijelo je fizička veličina, koja je određena odnosom vektora elementarne rotacije i trajanja ove rotacije. Smjer vektora može se odrediti pravilom desnog vijka duž osi O. U skalarnom obliku:
ω = dφ / dt.
Ako je ω = dφ / dt = const, tada se takav pokret naziva ravnomjernim rotacijskim gibanjem. Kada je kutna brzina određena formulom
ω = t / t.
Prema preliminarnoj formuli, dimenzija kutne brzine
[ω] = 1 rad / s.
Ravnomjerno rotacijsko gibanje tijela može se opisati periodom rotacije. Razdoblje rotacije T je fizička veličina koja određuje vrijeme koje je potrebno tijelu oko osi rotacije da izvede jednu potpunu revoluciju ([T] = 1 s). Ako u formuli za kutnu brzinu uzmemo t = T, 2 = 2 π (puni zavoj radijusa r), tada
ω = 2π / T,
stoga je razdoblje rotacije definirano kako slijedi:
T = 2π / ω.
Broj okretaja koje tijelo napravi po jedinici vremena naziva se frekvencija rotacije ν, koja je jednaka:
ν = 1 / T.
Frekvencijske jedinice: [ν] = 1 / c = 1 s -1 = 1 Hz.
Uspoređujući formule za kutnu brzinu i brzinu vrtnje, dobivamo izraz koji se odnosi na te veličine:
ω = 2πν.
Glavni elementi kinematike neujednačenog rotacijskog gibanja
Neujednačeno rotacijsko gibanje čvrste ili materijalne točke oko fiksne osi karakterizira njegovu kutnu brzinu, koja se mijenja s vremenom.
Vektor ε , koji karakterizira brzinu promjene kutne brzine, naziva se vektor kutnog ubrzanja:
ε = dω / dt.
Ako se tijelo okreće, ubrzavajući, dakle dω / dt> 0 , vektor ima smjer duž osi u istom smjeru kao i.
Ako je rotacijsko gibanje sporo - dω / dt <0 , tada su vektori ε i ω suprotno usmjereni.
Napomena. Kada dođe do neujednačenog rotacijskog kretanja, vektor ω može se mijenjati ne samo po veličini, već iu smjeru (kada se rotira os rotacije).
Odnos veličina koje karakteriziraju translacijsko i rotacijsko gibanje
Poznato je da je dužina luka s kutom rotacije radijusa i njegova vrijednost povezana s
ΔS = Δφ r.
Zatim linearnu brzinu materijalne točke koja izvodi rotacijsko gibanje
υ = ΔS / Δt = Δφr / Δt = ωr.
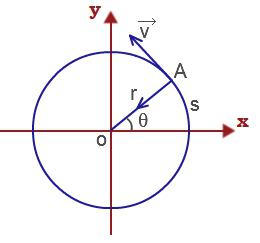
Normalno ubrzanje materijalne točke koja se odvija rotacijski kretanje naprijed definiramo kako slijedi:
a = υ 2 / r = ω 2 r2 / r.
Dakle, u skalarnom obliku
a = ω2r.
Tangencijalna ubrzana materijalna točka koja obavlja rotacijsko gibanje
a = ε r.
Trenutak zamaha materijalne točke
Vektorski proizvod polumjera vektora putanje materijalne točke mase m i njegovim momentom naziva se kutni moment ove točke u odnosu na os rotacije. Smjer vektora može se odrediti pomoću pravila desnog vijka.
Trenutak momenta materijalne točke ( L i ) usmjeren je okomito na ravninu nacrtanu kroz r i i υ i formira desna tri vektora s njima (to jest, kada se kreće s kraja vektora r i na v i, desni vijak pokazuje smjer vektora L i ).
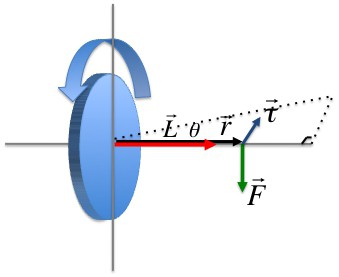
U skalarnom obliku
L = m i υ i r i sin (υ i , r i ).
Uzimajući u obzir da su pri kretanju u krug, vektor radijusa i vektor linearne brzine za i-tu materijalnu točku međusobno okomiti,
sin (υ i , r i ) = 1.
Tako će kutni moment materijalne točke za rotacijsko gibanje poprimiti oblik
L = m i υ i r i .
Trenutak sile koji djeluje na i-tu materijalnu točku
Vektorski proizvod radijusa-vektora, koji se drži na mjestu primjene sile, ovom silom naziva se momentom sile koja djeluje na i-tu materijalnu točku u odnosu na os rotacije.
U skalarnom obliku
M i = r i F i sin (r i , F i ).
Pod pretpostavkom da je r i sinα = l i , Mi i = l i F i .
Vrijednost l i jednaka duljini okomice koja je spuštena od točke rotacije do smjera sile, naziva se rame sile F i .
Rotacijska dinamika
Jednadžba dinamike rotacijskog gibanja zapisana je kao:
M = dL / dt.
Tekst zakona je sljedeći: brzina promjene kutnog momenta tijela, koja se rotira oko fiksne osi, jednaka je rezultirajućem trenutku oko te osi svih vanjskih sila koje se primjenjuju na tijelo.
Trenutak impulsa i moment inercije
Poznato je da za i-tu materijalnu točku kutni moment u skalarnom obliku daje formula
L i = m i υ i r i .
Ako umjesto linearnih brzina zamijeni svoj izraz kroz kutni:
υ i = ωr i ,
tada izraz za kutni moment dobiva oblik
L i = m i r i 2 ω.
Količina I i = m i r i 2 naziva se momentom inercije oko osi i-te materijalne točke apsolutno krutog tijela koje prolazi kroz njegovo središte mase. Zatim kutni moment materijalne točke koju pišemo:
L i = I i ω.
Trenutak impulsa apsolutno krutog tijela zapisuje se kao zbroj impulsnih trenutaka materijalnih točaka koje čine ovo tijelo:
L = Iω.
Trenutak sile i moment inercije
Zakon rotacijskog gibanja glasi kako slijedi:
M = dL / dt.
Poznato je da predstavlja trenutak impuls tijela moguće kroz trenutak inercije:
L = Iω.
tada
M = Ido / dt.
S obzirom da je kutno ubrzanje određeno izrazom
ε = dω / dt,
dobivamo formulu za trenutak sile koju predstavlja trenutak inercije:
M = Iε.
Napomena. Trenutak sile smatra se pozitivnim ako je kutno ubrzanje kojim je uzrokovano veće od nule, i obrnuto.
Steinerova teorema. Zakon zbrajanja trenutaka inercije
Ako je os rotacije tijela kroz središte mase ne prolazi, onda u odnosu na tu osovinu možete pronaći njegov moment inercije prema Steinerovom teoremu:
I = I 0 + ma 2 ,
gdje I 0 - početni moment inercije tijela; m je tjelesna masa; a je udaljenost između osi.
Ako se sustav, koji se vrti oko fiksne osi, sastoji od n tijela, tada će ukupni moment inercije ovog tipa sustava biti jednak zbroju trenutaka koji ga čine (zakon zbrajanja momenta inercije).