Fibonaccijev slijed i načela Zlatnog odjeljka
Fibonaccijev slijed, koji je postao poznat većini kroz film i knjigu Da Vincijeve šifre, je niz brojeva izvedenih od talijanskog matematičara Leonarda iz Pise, poznatijeg pod pseudonimom Fibonacci, u 13. stoljeću. Sljedbenici znanstvenika primijetili su da formula u kojoj je ovaj niz brojeva podređen pronalazi svoj odraz u svijetu oko nas i rezonira s drugim matematičkim otkrićima, otvarajući nam vrata za tajne svemira. U ovom članku opisat ćemo što je Fibonaccijev slijed, razmotriti primjere mapiranja ovog obrasca u prirodi i usporediti ga s drugim matematičkim teorijama. 
Formulacija i definicija
Fibonaccijev niz je matematički slijed, čiji je svaki element jednak zbroju prethodna dva. Neka neki član sekvence bude xn. Tako dobivamo formulu koja vrijedi za cijelu seriju: xn + 2 = xn + xn + 1. S ovim redoslijedom slijeda će izgledati ovako: 1, 1, 2, 3, 5, 8, 13, 21, 34. Sljedeći broj će biti 55, budući da je zbroj 21 i 34 55. I tako dalje na istom principu.
Primjeri u okolišu
Ako pogledamo biljku, osobito na krunu lišća, napominjemo da oni cvjetaju u spirali. Kutovi se formiraju između susjednih listova, koji, pak, čine ispravan matematički Fibonacci niz. Zahvaljujući ovoj značajki, svaki pojedinačni list koji raste na stablu prima maksimalnu količinu sunčeve svjetlosti i topline. 
Fibonacci matematički puzzle
Poznati matematičar predstavio je svoju teoriju kao zagonetku. Zvuči kako slijedi. Možete staviti par zečeva u zatvoreni prostor kako biste saznali koliko će se parova zečeva roditi u roku od jedne godine. S obzirom na prirodu tih životinja, činjenica da je svaki mjesec par sposoban proizvesti novi par, a spremni su za razmnožavanje nakon što su dostigli dva mjeseca, na kraju je dobio svoj poznati broj brojeva: 1, 1, 2, 3, 5, 8 , 13, 21, 34, 55, 89, 144 - gdje je prikazan broj novih parova kunića u svakom mjesecu.
Fibonacci niz i proporcionalni omjer
Ova serija ima nekoliko matematičkih nijansi koje svakako trebate uzeti u obzir. On, koji se približava sporije i sporije (asimptotski), teži nekom proporcionalnom omjeru. Ali to je iracionalno. Drugim riječima, to je broj s nepredvidivim i beskonačnim slijedom decimalnih brojeva u djelomičnom dijelu. Primjerice, omjer bilo kojeg elementa serije varira oko broja 1.618, a zatim nadmašuje, a zatim ga doseže. Sljedeće po analogiji približava se 0,618. Što je obrnuto proporcionalno broju 1.618. Ako dijelimo elemente kroz jedan, dobivamo 2.618 i 0.382. Kao što ste već razumjeli, one su također obrnuto proporcionalne. Dobiveni brojevi se nazivaju Fibonaccijevi koeficijenti. A sada ćemo objasniti zašto smo izvršili te izračune. 
Zlatni omjer
Razlikujemo sve objekte oko nas prema određenim kriterijima. Jedna od njih je forma. Neki od nas privlače više, neki manje, a neki ne. Primijećeno je da je simetrični i proporcionalni objekt mnogo lakše percipiran od strane čovjeka i izaziva osjećaj sklada i ljepote. Cjelokupna slika uvijek uključuje dijelove različitih veličina koji su u određenom međusobnom omjeru. Otuda i odgovor na pitanje što se zove Zlatni dio. Ovaj koncept znači savršenstvo odnosa između cjeline i dijelova u prirodi, znanosti, umjetnosti i S matematičkog stajališta, razmotrite sljedeći primjer. Uzmite segment bilo koje duljine i podijelite ga na dva dijela tako da se manji dio odnosi na veći kao na sumu (duljinu cijelog segmenta) na veću. Dakle, uzimamo segment c za vrijednost jedne. Njegov dio a bit će jednak 0.618, drugi dio b , ispada, jednak je 0.382. Stoga se pridržavamo uvjeta Zlatni dio. Omjer segmenta c prema a jednak je 1,618. A omjer dijelova c i b je 2.618. Dobili smo Fibonaccijeve koeficijente koji su nam već poznati. Po istom principu grade se zlatni trokut, zlatni pravokutnik i zlatni kvadar. Također je vrijedno spomenuti da je proporcionalni omjer dijelova ljudskog tijela blizak Zlatnom omjeru. 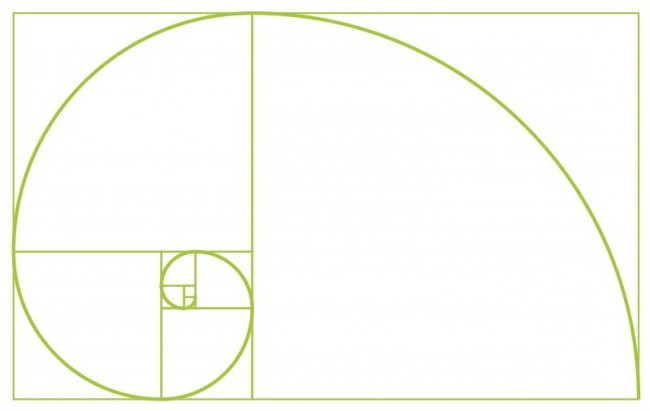
Je li Fibonacci slijed svega?
Pokušajmo kombinirati teoriju Zlatne sekcije i poznate serije talijanskih matematičara. Počnimo s dva kvadrata prve veličine. Zatim na vrh dodamo još jedan kvadrat druge veličine. Hajde da nacrtamo pored iste figure s duljinom stranice jednakom zbroju dviju prethodnih strana. Isto tako nacrtajte kvadrat pete veličine. I tako možete nastaviti neograničeno dok vam ne postane dosadno. Glavno je da je veličina strane svakog sljedećeg kvadrata jednaka zbroju vrijednosti strana dviju prethodnih. Dobivamo niz poligona čija je duljina Fibonaccijevi brojevi. Ove brojke se nazivaju Fibonaccijevi pravokutnici. Hajde da nacrtamo glatku liniju kroz uglove naših poligona i dobijemo ... Arhimedovu spiralu! Povećanje visine ove figure, kao što znate, uvijek je jednako. Ako uključite fantaziju, tada se rezultirajuća slika može povezati s školjkom školjke. Iz toga možemo zaključiti da je Fibonaccijev slijed temelj proporcionalnih, skladnih omjera elemenata u okolnom svijetu. 
Matematički slijed i svemir
Ako bolje pogledate, tada se Arhimedova spirala (negdje eksplicitno, ali negdje prikriveno) i stoga Fibonacci princip može pratiti u mnogim uobičajenim prirodnim elementima koji okružuju osobu. Na primjer, ista školjka školjke, cvjetovi brokule, cvijet suncokreta, konus crnogorične biljke i slično. Ako pogledamo u stranu, vidjet ćemo Fibonaccijev niz u beskonačnim galaksijama. Čak i osoba, nadahnuta prirodom i usvajanjem njezina oblika, stvara objekte u kojima se može pratiti spomenuta serija. Sada je vrijeme da se prisjetimo Zlatne sekcije. Uz Fibonaccijev uzorak, prate se principi ove teorije. Postoji verzija da je Fibonaccijev slijed svojevrsni prirodni test koji se prilagođava savršenijem i temeljnijem logaritamskom slijedu Zlatnog odjeljka, koji je gotovo identičan, ali nema početka i beskonačan je. Priroda prirode je takva da mora imati vlastitu polaznu točku, iz koje treba graditi da bi stvorila nešto novo. Odnos prvih elemenata Fibonacci niza daleko je od načela Zlatnog odjeljka. Međutim, što ga dalje nastavljamo, to je više odstupanje izglađeno. Da bi se odredio redoslijed, potrebno je znati njegova tri elementa koji slijede jedni druge. Za Zlatnu sekvencu, dva su dovoljna. Budući da je i aritmetička i geometrijska progresija.
zaključak
Ipak, na temelju gore navedenog, možete postaviti prilično logična pitanja: "Odakle dolaze ti brojevi? Tko je autor cijelog svijeta koji ga je pokušao učiniti savršenim? Je li uvijek uvijek bilo onako kako je želio? Ako je tako, zašto je propao?" Što će se dalje dogoditi? Pronalaženje odgovora na jedno pitanje, dobivate sljedeće. Riješio sam ga - pojavljuju se još dva. Nakon što ih riješimo, dobivate još tri. Nakon što ih riješite, dobit ćete pet neriješenih. Onda osam, trinaest, dvadeset i jedan, trideset četiri, pedeset pet ...