Kako je formuliran i dokazan kosinusni teorem?
Ne svi učenici, a još više odrasli, znaju da je kosinusni teorem izravno povezan s Pitagorejskim teoremom. Točnije, potonji je poseban slučaj prvog. Ovaj trenutak, kao i dva načina za dokazivanje kosinusnog teorema, pomoći će vam da postanete osoba s više znanja. Osim toga, praksa izražavanja vrijednosti iz izvornih izraza je dobro razvijeno logičko mišljenje. Duga formula teorema o kojoj se govori sigurno će prisiliti čovjeka da radi i poboljšava se.
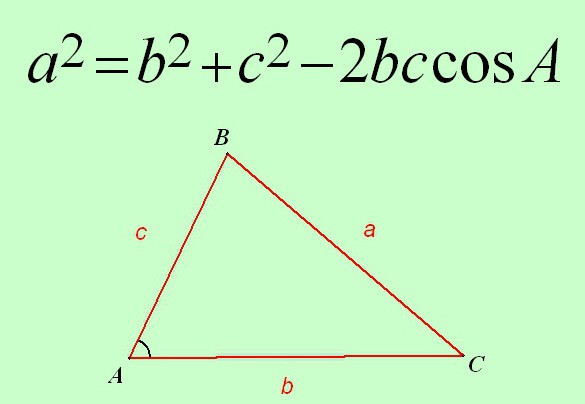
Početak razgovora: uvođenje simbola
Ovaj teorem je formuliran i dokazan za proizvoljni trokut. Stoga se uvijek može koristiti, u svakoj situaciji, ako su dane dvije strane, au nekim slučajevima tri, i kut, a ne nužno i između njih. štogod vrsta trokuta teorem uvijek radi.
I sada o označavanju količina u svim izrazima. Bolje je da se odmah složite, kako ne biste nekoliko puta objasnili. Za to je sastavljena sljedeća tablica.
| Element trokuta | Njegova oznaka |
| Nepoznata strana | i |
| Dvije druge strane | u, s |
| Kut nasuprot nepoznate strane | |
| Углы, которые лежат против других сторон Kutovi koji leže na drugim stranama | B, C |
| Visina vrha trokuta | n |
Formulacija i matematičko pisanje
Dakle, kosinusni teorem je formuliran na sljedeći način:
Kvadrat stranice bilo kojeg trokuta jednak je zbroju kvadrata druge dvije strane, minus dvostruko proizvod istih strana kosinusom kuta koji leži između njih.
Naravno, to je dugo, ali ako razumijete njegovu suštinu, bit će lako zapamtiti. Možete čak zamisliti crtež trokuta. Vizualno uvijek lakše pamtiti.
Formula ovog teorema će izgledati ovako:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Malo dugo, ali sve je logično. Ako pogledate malo bliže, možete vidjeti da se slova ponavljaju, tako da je lako zapamtiti.
Zajednički dokaz teorema
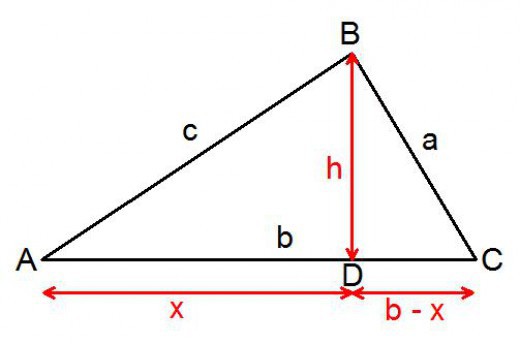
Budući da vrijedi za sve trokute, moguće je odabrati za rezoniranje bilo koji od tipova. Neka bude lik sa svim oštrim kutovima. Razmotrimo proizvoljan akutni trokut čiji je kut C veći od kuta B. Iz vrha s tim velikim kutom trebate spustiti okomitu na suprotnu stranu. Visina koja drži dijeli trokut na dva pravokutna. To je potrebno za dokaz.
Strana će biti podijeljena u dva segmenta: x, y. Potrebno ih je izraziti u poznatim terminima. Dio koji se ispostavi da je u trokutu s hipotenuza jednakom, izražava se pisanjem:
x = u * cos A.
Drugi će biti jednak toj razlici:
y = s - u * cos A.
Sada trebamo napisati Pitagorin teorem za ta dva desni trokuti na nepoznatoj visini. Ove formule izgledat će ovako:
n 2 = u 2 - (u * cos A) 2 ,
n 2 = a 2 - (c - c * cos A) 2 .
U tim jednakostima identični su izrazi s lijeve strane. Stoga će i njihove desne strane biti jednake. Lako je pisati. Sada morate otvoriti zagrade:
u 2 - u 2 * (cos A) 2 = a 2 - s 2 + 2 s * u * cos A - u 2 * (cos A) 2 .
Ako izvršimo prijenos i redukciju takvih pojmova, tada dobivamo početnu formulu, koja je napisana iza riječi, to jest, kosinusni teorem. Dokaz je potpun.
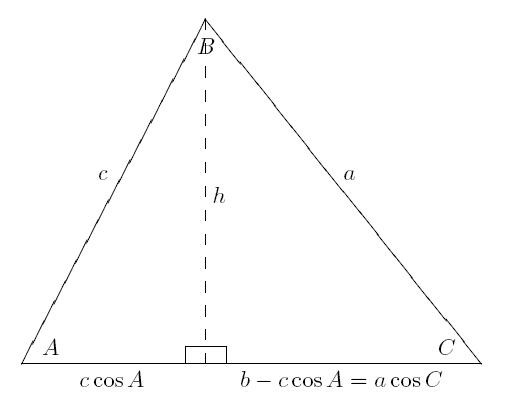
Dokaz teorema kroz vektore
Mnogo je kraći od prethodnog. A ako znate svojstva vektora, onda će se kosinusni teorem za trokut jednostavno dokazati.
Ako su strane a, b, c označene redom vektorima BC, AC i AB, tada je jednakost istinita:
SU = AC - AB.
Sada morate izvršiti neke radnje. Prva od njih je kvadriranje obje strane jednakosti:
BC 2 = AC 2 + AB 2 - 2 AC * AB.
Tada se jednakost mora prepisati u skalarnom obliku, s obzirom da je proizvod vektora jednak kosinusu kuta između njih i njihovih skalarnih vrijednosti:
BC 2 = AC 2 + AB 2 - 2 AC * AB * cos A.
Ostaje samo vratiti se na stari zapis, a opet će se pojaviti kosinusni teorem:
a 2 = 2 + s 2 - 2 * c * s * cos A.
Formule za druge strane i sve kutove
Da biste pronašli stranu, iz kosinusnog teorema morate izvući kvadratni korijen. Formula za kvadrate jedne od drugih strana će izgledati ovako:
s 2 = a 2 + do 2 - 2 * a * do * cos C.
Za pisanje izraza za kvadrat stranice, potrebno je zamijeniti prethodnu jednakost s od do, i obrnuto, i postaviti kut B pod kosinus.
Iz osnovne formule teorema možemo izraziti vrijednost kosinusa kuta A:
cos A = (u 2 + s 2 - a 2 ) / (2 v * s).
Formule za druge kutove izvedene su na isti način. Ovo je dobra praksa, pa ih možete i sami napisati.
Naravno, nema potrebe pamtiti ove formule. Dovoljno je razumjeti teorem i sposobnost izvođenja tih izraza iz njegovog glavnog zapisa.
Izvorna formula teorema omogućuje pronalaženje strane ako kut nije između dva poznata. Na primjer, trebate pronaći u , kada se daju vrijednosti: a, c, a . Ili je nepoznat s , ali postoje vrijednosti a, b, a .
U toj situaciji morate premjestiti sve formule dodatka ulijevo. Ova jednakost je dobivena:
s 2 - 2 * v * s * cos A + v 2 - a 2 = 0.
Ponovno ga napišite u nešto drugačijem obliku:
s 2 - (2 * u * cos A) * s + (u 2 - i 2 ) = 0.
Lako možete vidjeti kvadratnu jednadžbu. U njemu je nepoznata količina c , a sve ostale su dane. Stoga je dovoljno riješiti ga uz pomoć diskriminanta. Tako će se naći nepoznata strana.
Slično tome, dobiva se formula za drugu stranu:
2 - (2 * s * cos A) * c + (c 2 - a 2 ) = 0.
Iz drugih izraza, takve formule lako možete i sami nabaviti.
Kako izračunati kut bez izračunavanja kosinusa?
Ako bolje pogledate formulu kosinusnog kuta dobivenu ranije, primijetit ćete sljedeće:
- nazivnik dijela uvijek je pozitivan broj, jer sadrži proizvod strana koje ne mogu biti negativne;
- kut će ovisiti o znaku brojnika.
Kut A bit će:
- akutna u situaciji kada je brojnik veći od nule;
- tupi ako je taj izraz negativan;
- izravno kada je nula.
Usput, potonja situacija pretvara kosinusni teorem u Pitagorin teorem. Budući da je za kut od 90º, kosinus nula, a posljednji pojam nestaje.
Prvi zadatak
stanje
Tuzni kut nekog proizvoljnog trokuta je 120º. O stranama na koje je ograničen, poznato je da je jedna od njih 8 cm dulja od druge, poznata je duljina treće strane, 28 cm, a potrebno je pronaći perimetar trokuta.
odluka
Prvo morate označiti jednu od strana slovom "x". U tom slučaju, drugi će biti jednak (x + 8). Budući da postoje izrazi za sve tri strane, možete koristiti formulu koju daje kosinusni teorem:
28 2 = (x + 8) 2 + x 2 - 2 * (x + 8) * x * cos 120º.
U tablicama za kosinus, morate pronaći vrijednost koja odgovara 120 stupnjeva. To će biti broj 0,5 sa znakom minus. Sada je potrebno otvoriti zagrade, poštujući sva pravila i dati slične izraze:
784 = x 2 + 16x + 64 + x 2 - 2x * (-0,5) * (x + 8);
784 = 2x2 + 16x + 64 + x2 + 8x;
3x 2 + 24x - 720 = 0.
Ova kvadratna jednadžba rješava se pronalaženjem diskriminanta, koji će biti jednak:
D = 24 2 - 4 x 3 * (- 720) = 9216.
Budući da je njegova vrijednost veća od nule, jednadžba ima dva osnovna odgovora.
x 1 = ((-24) + √ (9216)) / (2 x 3) = 12;
x 2 = ((-24) - 9 (9216)) / (2 x 3) = -20.
Posljednji korijen ne može biti odgovor na problem, jer stranka mora nužno biti pozitivna.
Dakle, dvije strane su poznate. Lako je pronaći treći: 12 + 8 = 20 (cm). Sada možete odgovoriti na pitanje problema. Perimetar trokuta definira se kao zbroj svih strana:
24 + 12 + 20 = 60 (cm).
Odgovor : opseg je 60 centimetara.

Problem broj 2
stanje
U trokutu su poznati: c , jednaka 2 cm; a , koja je 10 cm; kut C vrijednost 120º. Potrebno je pronaći stranu.
odluka
Prvo morate koristiti kosinusni teorem i izvesti formulu kvadratna jednadžba u kojoj će vrijednost u biti nepoznata:
s 2 = a 2 + u 2 - 2 * a * u * cos C
i
u 2 - (2 * a * cos C) * u + (a 2 - c 2 ) = 0.
Potrebno je zamijeniti sve poznate vrijednosti u stanju:
u 2 - (2 * 10 * cos 120º) * u + (10 2 - 2 2 ) = 0.
Sada moramo brojati što je moguće kako bi pojednostavili izraz:
u 2 - (20 * (-1/2)) * u + (100 - 4) = 0
ili
u 2 + 10 * u - 96 = 0.
Ovo je standardna kvadratna jednadžba koju treba riješiti pronalaženjem diskriminantne:
D = (10) 2 - 4 * 1 * (-96) = 484.
Prema formulama morate napraviti izračune za nepoznatu stranu:
u 1 = (- 10 + 22) / 2 = 6 (cm);
u 2 = (- 10 - 22) / 2 = - 16 - ovaj korijen ne zadovoljava rješenje problema, jer strana ne može biti negativna.
Odgovor: nepoznata strana je 6 cm.
Treći zadatak
stanje
U nekom trokutu prikazane su strane: a, b, c , koje su 6 cm, 10 cm i 8 cm, a potrebno je izračunati kut A.
odluka
Opet morate koristiti kosinusni teorem. Upotrijebljen je njezin zapis u kojem se nalazi kosinus kuta A, budući da upravo to treba izračunati. Evo formule za kosinus nepoznatog kuta:
cos A = (u 2 + s 2 - a 2 ) / (2 v * s).
Ostaje zamjena vrijednosti stranaka i izvršavanje svih izračuna:
cos A = (10 2 + 8 2 - 6 2 ) / (2 x 8 x 10).
Nakon što su svi pojmovi kvadrirani i množite brojeve iz imenitelja:
cos A = (100 + 64 - 36) / (160).
Nakon dodavanja i podjele ispada:
cos A = 128/160 = 0,8.
Sada trebate koristiti tablicu Bradis da biste saznali koji je kut A. jednak. Najbliža vrijednost kuta za kosinus je 36º54´.
Odgovor: vrijednost kuta A je 36º54´.