Interpolacija je ... Definicija, značajke izračuna i primjeri interpolacije

Mnogi od nas su se suočili s nerazumljivim pojmovima u različitim znanostima. No, vrlo je malo ljudi koji se ne boje nerazumljivih riječi, nego nas, naprotiv, potiču i prisiljavaju da se sve više i više bavimo predmetom koji se proučava. Danas ćemo govoriti o takvoj stvari kao što je interpolacija. To je metoda konstruiranja grafova iz poznatih točaka, koja omogućuje, s minimalnom količinom informacija o funkciji, predviđanje njezina ponašanja na određenim dijelovima krivulje.

Prije nego što se okrenemo suštini same definicije i podrobnije ispričamo o njoj, malo se upustimo u priču.

Povijest

Interpolacija je poznata još od antičkih vremena. Međutim, ovaj fenomen svoj razvoj duguje nekoliko najistaknutijih matematičara prošlosti: Newton, Leibniz i Gregory. Razvili su ovaj koncept uz pomoć naprednijih matematičkih metoda dostupnih u to vrijeme. Prije toga, naravno, korištena je i korištena interpolacija u izračunima, ali to je učinjeno u potpuno netočnim načinima koji zahtijevaju veliku količinu podataka za izradu modela koji je više ili manje blizu stvarnosti.

Danas možemo odabrati čak i koji je način interpolacije prikladniji. Sve je prevedeno na računalni jezik, koji s velikom točnošću može predvidjeti ponašanje funkcije u određenom području, ograničeno poznatim točkama.

Interpolacija je prilično uski pojam, stoga njegova povijest nije toliko bogata činjenicama. U sljedećem poglavlju shvatit ćemo što je zapravo interpolacija i kako se ona razlikuje od njezine suprotnosti - ekstrapolacija.

Što je interpolacija?

Kao što smo rekli, ovo je opći naziv za načine izgradnje grafikona po točkama. U školi se to uglavnom radi sastavljanjem tablice, identificiranjem točaka na grafikonu i grubim izgradnjom linija koje ih povezuju. Posljednje je djelovanje napravljeno na temelju razmatranja sličnosti istraživane funkcije s drugima, vrste grafova koje poznajemo.

Međutim, postoje i drugi, složeniji i točniji načini za ostvarivanje zadatka ucrtavanja po točkama. Dakle, interpolacija je zapravo "predviđanje" ponašanja funkcije u određenom području, ograničeno poznatim točkama.

Sličan koncept povezan je s istim područjem - ekstrapolacijom. On također predstavlja predviđanje grafa funkcije, ali izvan poznatih točaka grafikona. S ovom metodom, predviđanje se vrši na temelju ponašanja funkcije na poznatom intervalu, i tada se ta funkcija također primjenjuje na nepoznati interval. Ova metoda je vrlo pogodna za praktičnu uporabu i aktivno se koristi, na primjer, u ekonomiji za predviđanje uspona i padova na tržištu te za predviđanje demografske situacije u zemlji.

Ali smo se odmaknuli od glavne teme. U sljedećem poglavlju shvatit ćemo kakva se interpolacija događa i pomoću koje formule možete izvesti ovu operaciju.

Vrste interpolacije

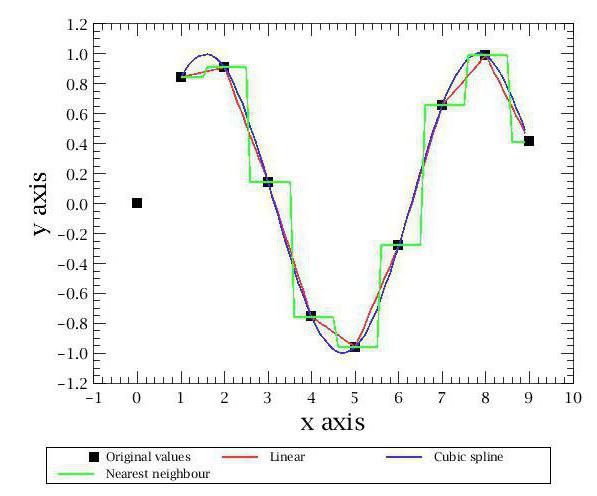
Najjednostavniji tip je interpolacija najbližeg susjeda. Ovom metodom dobivamo vrlo približan graf koji se sastoji od pravokutnika. Ako ste barem jednom vidjeli objašnjenje geometrijskog značenja integrala na grafu, tada ćete razumjeti o kakvom se grafičkom obliku radi.

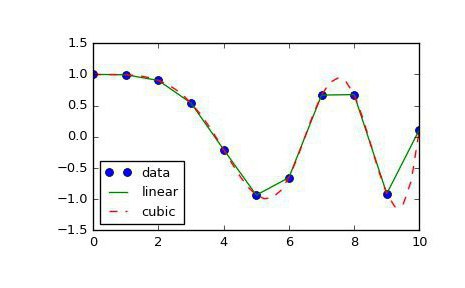
Osim toga, postoje i druge metode interpolacije. Najpoznatiji i najpopularniji su povezani s polinomima. Oni su točniji i omogućuju vam da predvidite ponašanje funkcije s prilično lošim skupom vrijednosti. Prva metoda interpolacije koju smatramo će biti linearna interpolacija polinomima. To je najlakši način iz ove kategorije, a svakako je svatko od vas to koristio u školi. Njezina je bit u izgradnji ravnih linija između poznatih točaka. Kao što je poznato, jedna pravac prolazi kroz dvije točke ravnine čija se jednadžba može pronaći na temelju koordinata tih točaka. Konstruirajući ove ravne linije, dobivamo slomljeni grafikon, koji je nekako, ali odražava približne vrijednosti funkcija i općenito se podudara sa stvarnošću. Time se izvodi linearna interpolacija.

Komplicirani tipovi interpolacije

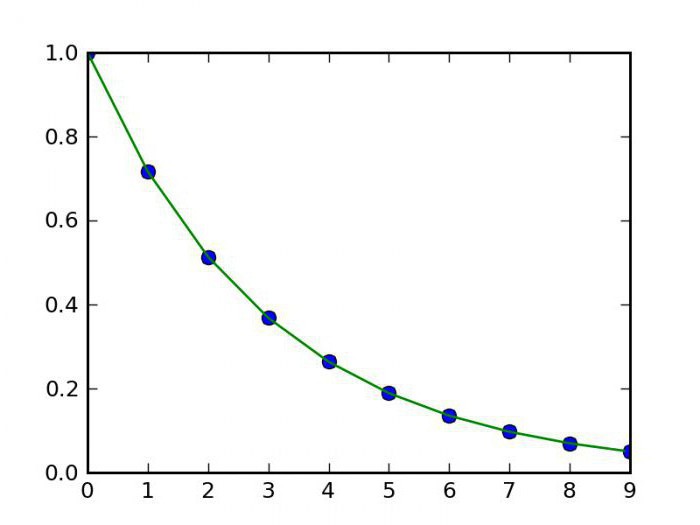
Postoji još zanimljivija, ali složenija metoda interpolacije. Izumio ga je francuski matematičar Joseph Louis Lagrange. Zato je izračunavanje interpolacije korištenjem ove metode nazvano po njemu: Lagrangeova interpolacija. Fokus ovdje je sljedeći: ako metoda opisana u prethodnom odlomku koristi samo linearnu funkciju za izračun, tada Lagrangeova dekompozicija također uključuje uporabu polinoma viših stupnjeva. Ali nije lako pronaći same formule za interpolaciju za različite funkcije. I što je više točaka poznato, to je preciznija formula za interpolaciju. Ali postoji mnogo drugih metoda.

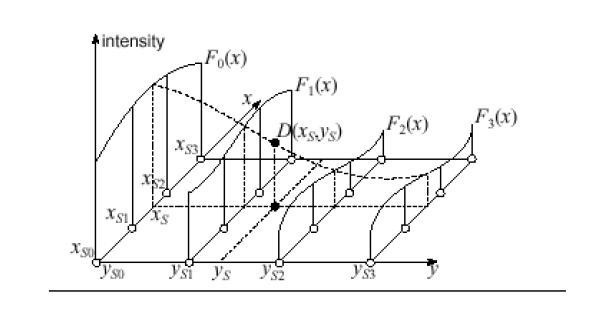
Tu je i savršenija i realnija metoda izračuna. Formula za interpolaciju koja se u njoj koristi jest skup polinoma, čija primjena ovisi o području funkcije. Ova metoda se naziva spline funkcija. Osim toga, postoje i načini za izvođenje takve funkcije kao što su interpolacijske funkcije dviju varijabli. Postoje samo dvije metode. Među njima, bilinearna ili dvostruka interpolacija. Ova metoda omogućuje vam da lako izradite grafikon točkama trodimenzionalni prostor. Ostale metode neće utjecati. Općenito, interpolacija je univerzalni naziv za sve ove metode grafičkoga prikazivanja, ali raznovrsnost načina na koje se to može izvesti prisiljava ih da se podijele u grupe ovisno o vrsti funkcije koja je predmet ove akcije. To jest, interpolacija, čiji smo primjer razmatrali gore, odnosi se na izravne metode. Tu je i inverzna interpolacija, koja se razlikuje u tome što nam omogućuje da izračunamo ne izravnu, već inverznu funkciju (tj. X od y). Nećemo razmatrati najnovije opcije, jer je to prilično teško i zahtijeva dobru matematičku bazu znanja.

Okrećemo se možda jednom od najvažnijih dijelova. Iz nje učimo kako i gdje se skup metoda koje raspravljamo primjenjuje u životu.

primjena

Matematika je poznata kao kraljica znanosti. Stoga, čak i ako prvo ne vidite točku u određenim operacijama, to ne znači da su beskorisne. Na primjer, čini se da je interpolacija beskorisna stvar, uz pomoć koje se mogu izgraditi samo grafikoni, što malo ljudi sada treba. Međutim, za bilo koje kalkulacije u inženjerstvu, fizici i mnogim drugim znanostima (na primjer, biologiji) iznimno je važno prikazati prilično potpunu sliku pojave, uz određeni skup vrijednosti. Vrijednosti raspršene na grafikonu ne daju uvijek jasnu predodžbu o ponašanju funkcije u određenom području, o vrijednostima njezinih derivata i točkama sjecišta s osima. I to je vrlo važno za mnoga područja našeg života s vama.

I kako je to korisno u životu?

Na ovo pitanje je vrlo teško odgovoriti. Ali odgovor je jednostavan: nema načina. To vam znanje neće biti korisno. Ali ako razumijete ovaj materijal i metode kojima se ta djela provode, vježbat ćete svoju logiku, koja je vrlo korisna u životu. Glavna stvar nije samo znanje, već vještine koje osoba stječe u procesu učenja. Uostalom, nije ni čudo što postoji izreka: "Živi i uči".

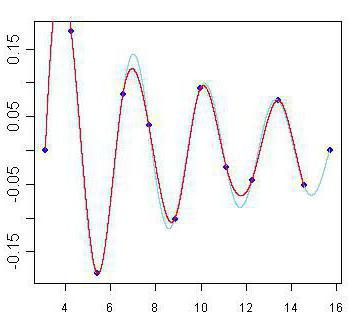
Srodni pojmovi

Za sebe možete razumjeti koliko je važno (i još uvijek ne gubi na važnosti) ovo područje matematike, promatrajući raznolikost drugih pojmova vezanih uz to. Već smo govorili o ekstrapolaciji, ali postoji i aproksimacija. Možda ste već čuli tu riječ. U svakom slučaju, što to znači, također smo raspravljali u ovom članku. Aproksimacija, kao i interpolacija, je koncept koji se odnosi na konstrukciju grafova funkcija. Ali razlika između prvog i drugog je u tome što predstavlja približnu konstrukciju grafa na temelju sličnih poznatih grafova. Ova dva pojma su vrlo slična jedni drugima, a zanimljivije je proučiti svaku od njih.

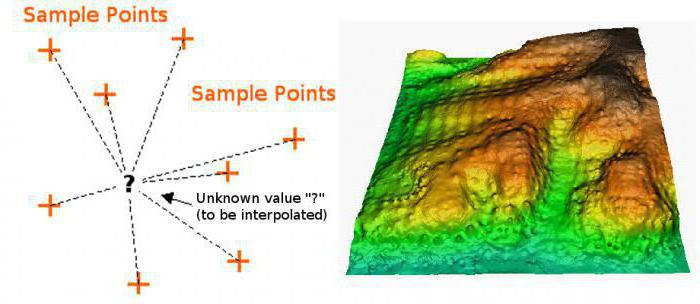
zaključak

Matematika nije tako složena znanost kao što se čini na prvi pogled. To je prilično zanimljivo. I u ovom članku pokušali smo vam to dokazati. Pogledali smo koncepte vezane za planiranje, naučili smo što je dvostruka interpolacija i pogledali primjere gdje se koristi.