Što je gravitacijska konstanta?
Nakon proučavanja fizike u umovima učenika sve vrste trajnih i njihovih vrijednosti. Tema gravitacije i mehanike nije iznimka. Najčešće ne mogu odgovoriti na pitanje koliko je važna gravitacijska konstanta. Ali oni će uvijek nedvosmisleno odgovoriti da je ona prisutna u zakonu svjetske širine.
Iz povijesti gravitacijske konstante
Zanimljivo je da u Newtonovim djelima nema takve veličine. U fizici se pojavila mnogo kasnije. Točnije, to je bilo tek početkom devetnaestog stoljeća. Ali to ne znači da nije. Znanstvenici ga jednostavno nisu identificirali i nisu prepoznali njegovo točno značenje. Govoreći o značenju. gravitacija konstantno stalno kako je navedeno decimal s velikim brojem znamenki iza decimalne točke, ispred koje je nula.
Upravo zato što ta količina pretpostavlja tako malu vrijednost, učinak sile gravitacije je neprimjetan na mala tijela. Upravo zbog tog množitelja, sila privlačnosti ispada da je zanemariva.
Prvi put je eksperimentalno ustanovio vrijednost koju je preuzela gravitacijska konstanta, fizičar G. Cavendish. I to se dogodilo 1788.

U svojim je pokusima koristio tanku šipku. Bila je obješena na tanku bakrenu žicu i imala je duljinu od oko 2 metra. Na krajeve ove šipke pričvršćene su dvije identične olovne kuglice promjera 5 cm, a pored njih su postavljene velike olovne kuglice. Promjer im je već bio 20 cm.
Pri približavanju velikih i malih kuglica, promatrana je rotacija štapa. Govorio je o njihovoj privlačnosti. Iz poznatih masa i udaljenosti, kao i izmjerene sile uvijanja, bilo je moguće sasvim točno saznati što je gravitacijska konstanta jednaka.
Sve je počelo slobodnim padom tijela.
Ako stavimo tijela različite mase u prazninu, tada će pasti u isto vrijeme. Pod uvjetom da padaju s iste visine i počnu istodobno. Bilo je moguće izračunati ubrzanje kojim sva tijela padaju na Zemlju. Pokazalo se da je približno jednako 9,8 m / s2.
Znanstvenici su otkrili da je sila kojom se sve privlači na Zemlju uvijek prisutna. I to ne ovisi o visini do koje se tijelo kreće. Jedan metar, kilometar ili stotine kilometara. Bez obzira koliko je daleko tijelo, privući će ga Zemlja. Drugo pitanje je kako će njegova vrijednost ovisiti o udaljenosti?
Na to je pitanje odgovorio engleski fizičar I. Newton.
Smanjenje sile privlačenja tijela njihovom udaljenosti
Za početak, sugerirao je da se sila gravitacije smanjuje. I njegova je vrijednost obrnuto povezana s kvadratom udaljenosti. Štoviše, ta se udaljenost mora računati od središta planeta. Napravio je teoretske izračune.
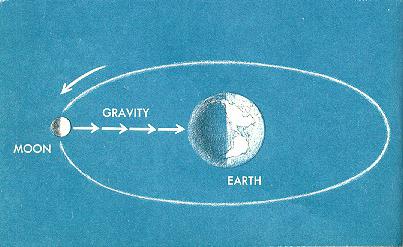
Tada je ovaj znanstvenik koristio podatke astronoma o kretanju prirodnog satelita Zemlje - Mjeseca. Newton je izračunao ubrzanje kojim se okreće oko planeta i dobio iste rezultate. To je svjedočilo o istinitosti njegova razmišljanja i dopušteno je formulirati zakon svijeta. Gravitacijska konstanta u njegovoj formuli do sada nije bila prisutna. U ovoj fazi bilo je važno odrediti ovisnost. Što je učinjeno. Gravitacija se smanjuje obrnuto od kvadratne udaljenosti od središta planeta.
Zakonu svijeta
Newton je nastavio razmišljati. Budući da Zemlja privlači Mjesec, onda ga i sama privlači Sunce. Štoviše, sila takve privlačnosti također bi se trebala pokoravati zakonu koji je on opisao. A onda ga je Newton proširio na sva tijela svemira. Stoga naziv zakona uključuje riječ "univerzalno".
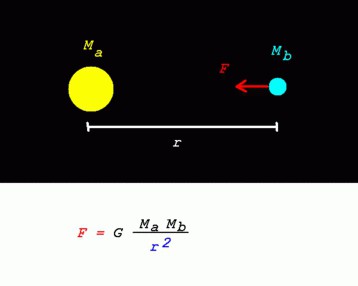
Snage svjetskih tijela definirane su kao proporcionalno ovisne o proizvodu masa i obrnuto od kvadrata udaljenosti. Kasnije, kada je određen koeficijent, formula zakona je dobila sljedeći oblik:
- Ft = G (m x x x m2): r2.
Sadrži sljedeći zapis:
| Sila gravitacije | F t |
| Gravitacijska konstanta | G |
| Masa tijela | m, m |
| Udaljenost između tijela | r |
Formula za gravitacijsku konstantu slijedi iz ovog zakona:
- G = (Ft X r 2 ): (m 1 x m 2 ).
Vrijednost gravitacijske konstante
Sada je došao red određenih brojeva. Budući da znanstvenici tu vrijednost stalno pojašnjavaju, različiti su brojevi službeno usvojeni u različitim godinama. Na primjer, prema podacima za 2008. godinu, gravitacijska konstanta iznosi 6,6742 x 10 -11 Nm 2 / kg 2 . Tri godine su prošle - i konstanta se broji. Sada je gravitacijska konstanta 6,6738 x 10 -11 Nm 2 / kg 2 . No, za školsku djecu u rješavanju problema, njezino zaokruživanje na takvu vrijednost je dopušteno: 6,67 x 10 -11 Nm 2 / kg 2 .
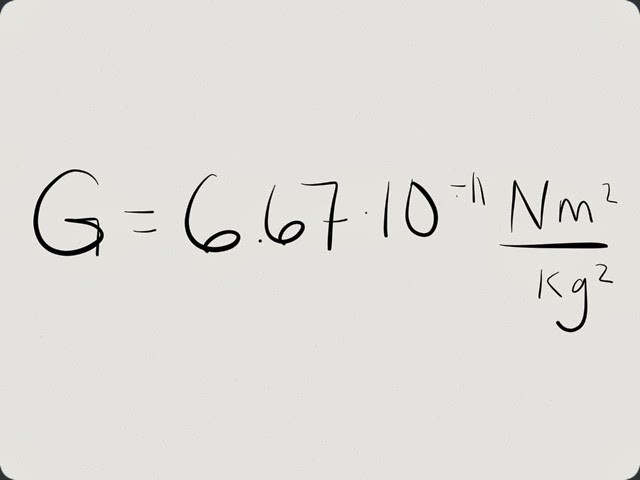
Koji je fizički smisao ovog broja?
Ako se u formuli, koja je dana zakonu svijeta, zamjenjuju konkretni brojevi, dobivate zanimljiv rezultat. U konkretnom slučaju, kada su mase tijela jednake 1 kilogramu, a nalaze se na udaljenosti od 1 metra, jačina sile jednaka je samom broju, koji je poznat po gravitacijskoj konstanti.
Odnosno, značenje gravitacijske konstante je to što pokazuje s kakvom će silom takva tijela biti privučena na udaljenosti od jednog metra. Po broju možete vidjeti koliko je ta sila mala. Uostalom, to je deset milijardi manje od jednog. Čak je i nemoguće primijetiti. Čak i sa povećanjem tijela stotinu puta rezultat se neće značajno promijeniti. I dalje ostaje mnogo manje od jednog. Stoga postaje jasno zašto je sila privlačenja vidljiva samo u onim situacijama ako barem jedno tijelo ima veliku masu. Na primjer, planet ili zvijezda.
Kako je gravitacijska konstanta s ubrzanjem slobodnog pada?
Ako usporedimo dvije formule, od kojih će jedna biti za gravitaciju, a drugu za zakon Zemlje, možemo vidjeti jednostavan uzorak. Gravitacijska konstanta, masa Zemlje i kvadrat udaljenosti od središta planete čine koeficijent koji je jednak ubrzati slobodan pad. Ako napišete ovu formulu, dobit ćete sljedeće:
- g = (GxM): r2.
I koristi sljedeći zapis:
| Masa Zemlje | M |
| Radijus Zemlje | r |
Usput, gravitacijska konstanta se može naći iz ove formule:
- G = (g x r 2 ): M.
Ako želite znati ubrzanje slobodnog pada na određenoj visini iznad površine planeta, onda je ova formula korisna:
- g = (G x M): (r + n) 2 , gdje je n visina iznad površine zemlje.
Zadaci koji zahtijevaju znanje o gravitacijskoj konstanti
Prvi zadatak
Stanje. Kakvo je ubrzanje slobodnog pada na jednom od planeta Sunčevog sustava, na primjer, na Marsu? Poznato je da je njegova masa 6,23 · 10 23 kg, a radijus planeta je 3,38 · 10 6 m.
Odluka . Morate koristiti formulu koja je napisana za Zemlju. Samo da u njemu zamijeni vrijednosti dane u zadatku. Pokazalo se da će ubrzanje slobodnog pada biti jednako proizvodu od 6,67 x 10 -11 i 6,23 x 10 23 , koji se tada mora podijeliti na kvadrat od 3,38 · 10 6 . U brojniku se dobiva vrijednost od 41,55 x 10 12 . A nazivnik će biti 11.42 x 10 12 . Stupnjevi će se smanjiti, pa je za odgovor dovoljno znati samo kvocijent dva broja.
Odgovor : 3,64 m / s 2 .
Zadatak dva
Stanje. Što treba učiniti s tijelima kako bi smanjili silu gravitacije za 100 puta?
Odluka . Kako se masa tijela ne može mijenjati, sila će se smanjiti zbog njihovog uklanjanja. Sto se dobiva iz kvadriranja 10. To znači da bi udaljenost između njih trebala biti 10 puta veća.
Odgovor : udaljite ih 10 puta od izvorne udaljenosti.