Pravokutni trapez: sve formule i primjeri zadataka
Zadaci s trapezom ne čine se teškim u brojnim slikama koje su ranije proučavane. Kao poseban slučaj razmatra se pravokutni trapezoid. A kada se traži njegovo područje, ponekad je pogodnije podijeliti ga na dva već poznata: pravokutnik i trokut. Treba samo malo razmisliti, i postoji rješenje.
Definicija pravokutnog trapeza i njegovih svojstava
Kod proizvoljnog trapeza, baze su paralelne, a strane mogu imati proizvoljnu vrijednost kutova prema njima. Ako se uzme u obzir pravokutni trapez, onda je u njemu jedna od strana uvijek okomita na baze. To znači da će dva ugla biti jednaka 90 stupnjeva. Štoviše, oni uvijek pripadaju susjednim vrhovima ili, drugim riječima, jednoj strani.
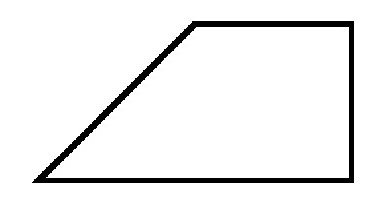
Ostali kutovi pravokutnog trapeza uvijek su oštri i tupi. I njihov će iznos uvijek biti jednak 180 stupnjeva.
Svaka dijagonala se oblikuje sa svojom manjom stranom pravokutni trokut. A visina, koja se izvlači s vrha s tupim kutom, dijeli lik na dva dijela. Jedan je pravokutnik, a drugi je pravi trokut. Usput, ova strana je uvijek jednaka visini trapeza.
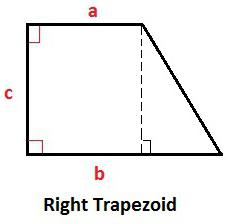
Koje su oznake prihvaćene u prikazanim formulama?
Sve vrijednosti koje se koriste u različitim izrazima koji opisuju trapez su prikladno odmah navedene i prikazane u tablici:
| vrijednost | Njegova oznaka |
| большее основание veća baza | |
| b | manja baza pravokutnog trapeza |
| c, h | okomito na osnovnu stranu, visinu |
| d | nagnuta strana |
| α | akutni kut |
| β | tup kut |
| m | trapezna srednja linija |
| d 1 | manja dijagonala |
| d 2 | velika dijagonala |
Formule koje opisuju elemente pravokutnog trapeza
Najjednostavniji od njih odnosi se na visinu i manju stranu:
c = h.
Neke formule za ovu stranu pravokutnog trapeza:
c = d * sinα;
c = (a - b) * tg α;
c = d (d2 - (a - b) 2 ).
Prvi slijedi iz pravog trokuta. I kaže da noga do hipotenuze daje sinus suprotnog kuta.
U istom trokutu druga noga jednaka je razlici dvije baze. Stoga je istinita tvrdnja koja izjednačava tangens kuta s omjerom nogu.
Iz istog trokuta može se izvesti formula koja se temelji na poznavanju Pitagorina teorema. Ovo je treći zabilježeni izraz.
Formule za drugu stranu mogu biti napisane. Oni su također tri:
d = (a - b) / cosα;
d = c / sin α;
d = √ (c 2 + (a - b) 2 ).
Prva dva se opet dobivaju iz omjera u istom pravokutnom trokutu, a drugi se izvodi iz Pitagoreanova teorema.
Koja se formula može koristiti za izračun površine?
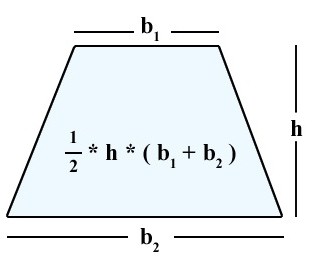
Ono što je dano za proizvoljni trapez. Samo je potrebno uzeti u obzir da je visina strana okomita na podloge.
S = (a + b) * h / 2.
Ove vrijednosti nisu uvijek izričito navedene. Dakle, za izračunavanje površine pravokutnog trapeza potrebno je izvršiti neke matematičke izračune.
Što ako trebate izračunati dijagonalu?
U tom slučaju morate vidjeti da oni tvore dva pravokutna trokuta. Stoga uvijek možete koristiti Pitagorin teorem. Tada će se prva dijagonala izraziti kao:
d1 = √ (c2 + b2)
ili na drugi način, zamjenjujući "s" s "h":
d1 = √ (h2 + b2).
Slično tome, dobivaju se formule za drugu dijagonalu:
d2 = √ (c2 + b2) ili d2 = √ (h2 + a2 ).
Problem broj 1
Stanje. Područje pravokutnog trapeza je poznato i iznosi 120 dm 2 . Visina mu je 8 dm. Potrebno je izračunati sve strane trapeza. Dodatni uvjet je da je jedna baza manja od druge za 6 dm.
Odluka. Budući da je dan pravokutni trapez, u kojem je visina poznata, možemo odmah reći da je jedna strana jednaka 8 dm, odnosno manja strana.
Sada možete računati drugo: d = √ (s 2 + (a - b) 2 ). I ovdje su obje strane i razlika u osnovama odmah dane. Potonji je 6 dm, to je poznato iz stanja. Tada će d biti jednako kvadratni korijen od (64 + 36), to jest, od 100. Tako je pronađena druga strana, jednaka 10 dm.
Zbroj baza može se pronaći iz formule za područje. Bit će jednaka dvostrukoj vrijednosti područja podijeljenom s visinom. Ako računate, ispada da je 240/8, tako da je zbroj baza 30 dm. S druge strane, njihova razlika je 6 dm. Kombinirajući ove jednadžbe, možemo računati obje baze:
a + b = 30 i a - b = 6.
Možete izraziti kao as (b + 6), zamijeniti ga u prvom jednakosti. Tada se ispostavi da će 2b biti jednako 24. Stoga će samo b biti 12 dm.
Tada je zadnja strana a jednaka 18 dm.
Odgovor je. Strane pravokutnog trapeza: a = 18 dm, b = 12 dm, c = 8 dm, d = 10 dm.
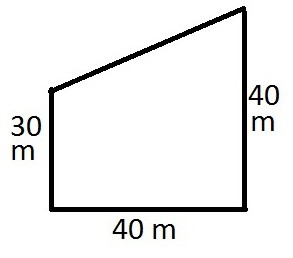
Problem broj 2
Stanje. S obzirom na pravokutni trapezoid. Njegova velika strana jednaka je zbroju baza. Njegova visina je 12 cm, izgrađen je pravokutnik čije su stranice jednake dnu trapeza. Potrebno je izračunati površinu ovog pravokutnika.
Odluka. Morate početi s željenim. Tražena površina određena je kao proizvod a i b. Obje ove količine nisu poznate.
Potrebno je koristiti dodatne jednakosti. Jedan od njih temelji se na tvrdnji iz uvjeta: d = a + b. Potrebno je upotrijebiti treću formulu za ovu stranu, koja je dana gore. Ispada: d 2 = c 2 + (a - b) 2 ili (a + b) 2 = c 2 + (a - b) 2 .
Potrebno je izvršiti transformaciju, zamjenjujući umjesto njezine vrijednosti uvjetom - 12. Nakon otvaranja zagrada i izlaganja takvih izraza, ispada da je 144 = 4 ab.
Na početku odluke rečeno je da a * b daje traženu površinu. Stoga u zadnjem izrazu ovaj proizvod možete zamijeniti s S. Jednostavan izračun će dati vrijednost područja. S = 36 cm2.
Odgovor je. Potrebna površina je 36 cm 2 .
Problem broj 3
Stanje. Područje pravokutnog trapeza 150√3 cm². Oštar kut je 60 stupnjeva. Kut između male baze i manje dijagonale ima istu vrijednost. Potrebno je izračunati manju dijagonalu.
Odluka. Iz svojstava trapeznih kutova ispada da je njegov tupi kut 120º. Tada ga dijagonala dijeli na jednaku, jer je jedan njezin dio već 60 stupnjeva. Tada je kut između ove dijagonale i druge baze također 60 stupnjeva. To znači da je trokut koji čini velika baza, nagnuta strana i manja dijagonala, jednakostraničan. Stoga će željena dijagonala biti jednaka a, kao i strana d = a.
Sada moramo razmotriti pravi trokut. U njemu je treći kut 30 stupnjeva. Dakle, noga koja leži uz nju jednaka je polovici hipotenuze. To znači da je manja baza trapeza jednaka polovici željene dijagonale: b = a / 2. Iz njega je potrebno pronaći visinu koja je jednaka bočnoj, okomitoj na baze. Strana sa ovdje je noga. Iz Pitagorina teorema:
c = (a / 2) * .3.
Sada ostaje samo zamjena svih vrijednosti u formuli područja:
150√3 = (a + a / 2) * (a / 2 * )3) / 2.
Rješavanje ove jednadžbe daje korijen od 20
Odgovor je. Manja dijagonala je 20 cm duga.