Sve suptilnosti kako izračunati područje paralelopipeda

Paralelepiped je najčešća figura među onima oko ljudi. Većina prostora je njegova. Posebno je važno znati za vrijeme popravka područje paralelopipeda, barem njegovih bočnih strana. Uostalom, morate znati točno koliko materijala kupiti.

Kakav je on?

To je prizma s četverokutnom bazom. Stoga ima četiri bočna lica koja su paralelogrami. To jest, takvo tijelo ima samo 6 lica.

Da bi se odredio paralelopiped u prostoru, on određuje površinu i volumen. Prvi može biti odvojeno za svako lice i za cijelu površinu. Osim toga, emitiraju više i samo bočna lica.

Koje su vrste paralelopipeda?

Sklon. Jedna u kojoj bočna lica oblikuju kut s bazom koja je različita od 90 stupnjeva. Njegovi gornji i donji četverokuti ne leže jedan nasuprot drugome, već su pomaknuti.

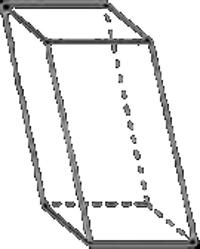
Izravno. Paralelopiped, čija su bočna lica pravokutnici, a na bazi je lik s proizvoljnim kutovima.

Pravokutni. Poseban slučaj prethodnog tipa: u bazi je pravokutnik.

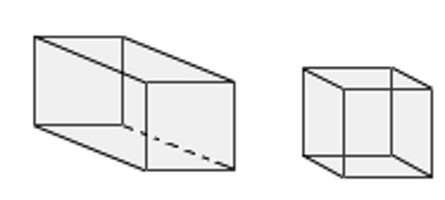
Kocka. Poseban tip paralelepipeda u kojem su sva lica predstavljena kvadratima.

Neke matematičke značajke paralelepipeda

Može doći do situacije kada su korisne u pronalaženju područja paralelepipeda.

• Rubovi koji leže jedan nasuprot drugome nisu samo paralelni, nego i jednaki.
• Dijagonala paralelepipednog sjecišta je podijeljena na jednake dijelove.
• U općenitijem slučaju, ako segment povezuje dvije točke na površini tijela i prolazi kroz sjecište dijagonala, tada se ta točka dijeli na pola.
• Za pravokutni paralelepiped vrijedi jednakost u kojoj u jednom dijelu postoji kvadrat dijagonale, au drugom - zbroj kvadrata njegove visine, širine i duljine.

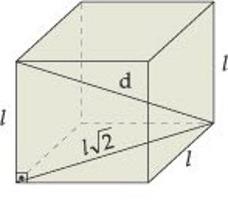
Kvadratni paralelipiped

Ako visinu tijela označimo kao "n", a osnovni perimetar sa slovom R _oc , onda se cijela bočna površina može izračunati pomoću formule:

S _strana = P _oc * n

Pomoću ove formule i određivanjem površine baze možemo izračunati ukupnu površinu:

S = S _strana + 2 * S _oc

U zadnjem unosu S _oc ., To jest, područje baze paralelepipeda, može se izračunati pomoću formule za paralelogram. Drugim riječima, trebate izraz u kojem trebate pomnožiti stranu i visinu spuštenu na nju.

Kvadratni paralelipiped

Usvojena je standardna oznaka duljine, širine i visine takvog tijela sa slovima "a", "b" i "c". Površina bočne površine izražava se formulom:

S _strana = 2 * s * (a + b)

Da bismo izračunali ukupnu površinu pravokutnog paralelepipeda, potreban nam je sljedeći izraz:

S = 2 * (aw + bs + kao)

Ako se ispostavi da je potrebno znati područje njegove baze, dovoljno je zapamtiti da je ovo pravokutnik, što znači da je dovoljno pomnožiti "a" i "c".

Kvadratna kocka

Njegova bočna površina formirana je s četiri kvadrata. Dakle, da biste ga pronašli, morate koristiti dobro poznatu formulu za kvadrat i pomnožiti je s četiri.

S _strana = 4 * a ²

A zbog činjenice da su njegove baze iste kvadrate, ukupna površina određena je formulom:

S = 6 * a ²

Kosi paralelepipedni kvadrati

Budući da su njegova lica paralelogrami, morate otkriti područje svake od njih i zatim ih saviti. Srećom, jednako je suprotno. Stoga morate izračunati područje samo tri puta, a zatim ih pomnožiti s dva. Ako ovo napišete u obliku formule, dobit ćete sljedeće:

S _strana = (S ₁ + S ₂ ) * 2,

S = (S1 + S2 + S3) * 2

Ovdje su S1 i S2 područja dviju bočnih strana, a S3 su baze.

Srodni zadaci

Prvi zadatak. Stanje. Trebate znati dužinu dijagonalna kocka, ako je površina cijele površine 200 mm2.

Odluka. Moramo početi dobivanjem izraza za željenu vrijednost. Njegov kvadrat jednak je trima kvadratima strane kocke. To znači da je dijagonala jednaka "a" pomnožena s korijenom od 3.

Ali strana kocke je nepoznata. Ovdje ćete morati iskoristiti činjenicu da je cijela površina poznata. Iz formule se ispostavlja da je "a" jednaka kvadratni korijen iz privatnih S i 6.

Ostaje samo brojati. Rub kocke je 200 (200/6), što je 10 / (3 (mm). Tada će dijagonala biti jednaka (10 / )3) * =3 = 10 (mm).

Odgovor je. Kocka dijagonale je 10 mm.

Drugi zadatak. Stanje. Potrebno je izračunati površina kocke, ako je poznato da je njegov volumen 343 cm2.

Odluka. Morat ćete koristiti istu formulu za područje kocke. Opet, opet je nepoznat rub tijela. Ali s obzirom na volumen. Iz formule za kocku je vrlo lako naučiti "a." Bit će jednako kubni korijen Jednostavan izračun daje vrijednost za rub: a = 7 cm.

Sada ostaje brojati njegov kvadrat i pomnožiti ga sa 6. a ² = 7 ² = 49, stoga će površina biti jednaka 49x6 = 294 (cm2).

Odgovor je. S = 294 cm2.

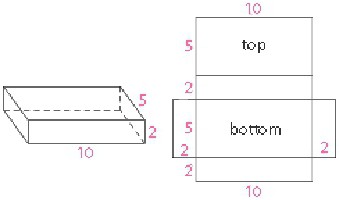
Treći zadatak. Stanje. Prikazana je pravilna četverokutna prizma s bazom od 20 dm. Potrebno je pronaći njegov bočni rub. Poznato je da je područje paralelepipeda jednako 1760 dm ² .

Odluka. Započnite razmišljanje pomoću formule za područje cijele površine tijela. Samo u njemu treba uzeti u obzir da su rubovi "a" i "b" jednaki. To proizlazi iz tvrdnje da je prizma ispravna. Dakle, u njegovoj osnovi leži četverokut s jednakim stranama. Stoga je a = c = 20 dm.

S obzirom na ovu okolnost, formula za područje je pojednostavljena na sljedeći način:

S = 2 * (a ² + 2c).

U njemu je sve poznato, osim željene vrijednosti "c", koja je upravo bočni rub paralelopipeda. Da biste ga pronašli, morate izvršiti konverziju:

• podijeliti svu nejednakost s 2;
• zatim pomaknite pojmove tako da lijevo bude 2as, a na desnoj je područje podijeljeno s 2 i kvadratić "a", a drugi je označen sa "-";
• zatim podijelite jednakost s 2a.

Rezultat je izraz:

c = (s / 2 - a ² ) / (2a)

Nakon zamjene svih poznatih vrijednosti i izvođenja radnji, ispada da je bočni rub jednak 12 dm.

Odgovor je . Bočni rub "c" je 12 dm.

Četvrti zadatak. Stanje. S obzirom na pravokutni paralelepiped. Jedno od njezinih lica ima površinu od 12 cm2. Potrebno je izračunati duljinu ruba, koja je okomita na ovo lice. Dodatni uvjet: volumen tijela je 60 cm3.

Odluka. Neka područje tog lica, koje se nalazi okrenuto prema promatraču, bude poznato. Ako se za označavanje uzimaju standardna slova za paralelopipedne dimenzije, tada će u podnožju rebra biti "a" i "b", a vertikalno - "c". Na temelju toga, područje poznatog lica definira se kao proizvod "a" na "c".

Sada morate koristiti poznati volumen. Njegova formula za pravokutni paralelopiped daje proizvod svih triju veličina: "a", "in" i "c". To jest, poznato područje, pomnoženo s "in", daje volumen. Odavde se pokazuje da se željeni rub može izračunati iz jednadžbe:

12 x = 60.

Elementarni izračun daje rezultat 5.

Odgovor je. Željeni rub je 5 cm.

Peti zadatak. Stanje. S obzirom na paralelopiped. U bazi je paralelogram sa stranama od 6 i 8 cm, a oštar kut između kojeg je 30º. Bočni rub ima duljinu od 5 cm, a potrebno je izračunati ukupnu površinu paralelepipeda.

Odluka. To je slučaj kada morate znati područje svih lica zasebno. Ili, točnije, tri para: baza i dvije strane.

Budući da se paralelogram nalazi u podnožju, njegova površina se izračunava kao produkt bočne strane i visine. Strana je poznata, ali visina nije. Mora se računati. To će zahtijevati oštru kutnu vrijednost. Visina se formira u paralelogramu pravokutni trokut. U njemu je noga jednaka proizvodu sinusa akutnog kuta, koji je suprotan hipotenuzi.

Neka poznata strana paralelograma bude "a". Tada će visina biti zapisana kao * sin 30º. Dakle, osnovna površina je a * c * sin 30º.

Sa bočnim rubovima sve je lakše. To su pravokutnici. Stoga je njihovo područje proizvod jedne strane na drugu. Prvi - a * s, drugi - u * s.

Ostaje kombinirati sve u jednu formulu i brojati:

S = 2 * (a * b * sin 30º + a * s + b * s)

Nakon zamjene svih količina, ispostavlja se da je tražena površina 188 cm ² .

Odgovor je. S = 188 cm2.